形态分量分析在齿轮箱复合故障诊断中的应用*

李 辉，郑海起，唐力伟

（1.石家庄铁路职业技术学院机电工程系 石家庄，050041）（2.军械工程学院一系 石家庄，050003）

引 言

由于齿轮箱具有传递运动准确、传递动力大和效率高的特点，在现代机械中应用广泛，因此对齿轮箱的故障检测与诊断具有重要的现实意义。目前，国内外学者对齿轮箱故障诊断方法进行了大量研究，最常用的方法是对从齿轮箱上测得的振动信号，在时域、频域或时频域内进行分析。常用的方法有快速傅里叶变换（FFT）、短时傅里叶变换（STFT）、Wigner－ville分布（WVD）［1］、小波变换（WT）［2－3］、Hilbert－Huang变换（HHT）［4－5］、Teager－Huang变换（THT）［6］等。在齿轮箱故障诊断研究中，大多是对齿轮箱的单一故障进行分析与诊断［2－6］，对齿轮箱复合故障诊断技术的研究较少；因此，复合故障诊断仍然是齿轮箱故障诊断的难点和热点问题［1－2］。近年来，为了对多分量的复杂信号进行分析，基于多种基函数的稀疏信号分解方法得到迅速发展，其中原子分解［7－10］（atom decomposition）和独立分量分析［11－12］（independent component analysis，简 称ICA）得到了广泛应用。传统的独立分量分析方法假设源信号是统计独立的，其结果是把信号分解成若干个相互独立的成分，虽然ICA方法在许多应用中［9－14］取得了较好的效果，但是ICA基于统计独立的假设条件，并不适用于所有的情况。Starck等［15－18］基于信号的稀疏表示和形态多样性，提出了形态分量分析（morphological component analysis，简称MCA）信号或图像处理方法。其基本思想是利用信号组成成分的形态差异性，不同的信号分量可以用不同的字典稀疏表示，其结果是把源信号分解成若干个形态各异的稀疏信号；因此，被分解出的诸分量具有实际的物理意义。形态分量分析方法已在图像处理［18－22］和医学信号分析［23］等领域得到了应用，且取得了较好的效果。

笔者提出了基于形态分量分析的齿轮箱复合故障诊断方法，并将其应用于齿轮箱轴承内圈、外圈、滚珠和齿轮齿面磨损故障特征信息的提取。仿真和实测齿轮箱振动信号分析结果表明：该方法能有效提取齿轮箱轴承和齿轮的故障特征，提高了齿轮箱复合故障诊断的有效性和准确性，其信号分离性能和降噪效果均优于经典的独立分量分析方法。

1 形态分量分析方法

1.1 形态分量分析的基本原理

对于任意的实信号s∈R，假设s为K个不同形态分量sk的线性组合，即，每个信号分量sk都存在着相对应的能够稀疏表示该信号分量的字典，即sk＝Φkαk。其中：Φk为过完备字典；αk为分解系数，且该字典仅能稀疏表示该信号分量，对于其他信号分量不能稀疏表示。s的稀疏分解［15］可以归结为求解如下优化问题

放宽式（1）中的约束条件，式（1）可转换为

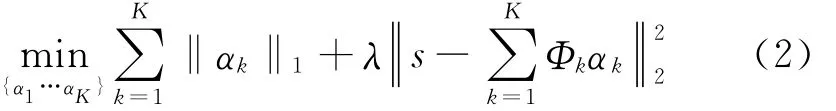
其中：λ为给定阈值。

根据sk＝Φkαk，给定sk，可以得到

根据式（3）和式（2），求解系数｛α1，α2，…，αK｝转化为求解信号分量｛s1，s2，…，sK｝

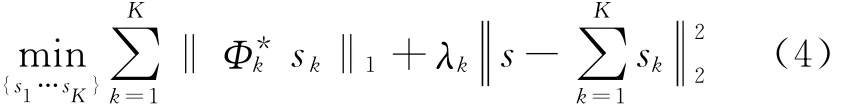
1.2 形态分量分析的步骤

根据式（4）的优化问题，Starck等［15］在块坐标松 驰 （block－coordinate－relaxation，简 称 BCR）方法［24］的基础上，给出了MCA的数值实现步骤。

1）给定最大迭代次数Lmax和阈值δk＝Lmaxλk／2；

2）当δk＞λk／2

for k＝1，2，…，K

假设sk′≠k和αk′不变，更新sk，计算残余量；计算αk＝ΦT＊rk；采用阈值法筛选αk，阈值为δk，得到分解系数；重构假设sk′和αk′≠k不变，更新

1.3 形态分量分析的阈值选择和更新方法

通过上面的分析可知：形态分量分析方法是通过迭代阈值算法实现的，即随着迭代次数的增加，阈值不断更新，当阈值小于给定的最小值δmin时，迭代终止。在MCA算法中，阈值的筛选方法和更新方法对算法的收敛速度有很大的影响，一个好的阈值方法必须具备以下3方面的要求［19］：a.具有适用性，能适合于各种不同的字典；b.低的计算量；c.不需要大量的迭代次数。在MCA算法中阈值的选择包括阈值筛选方法选择和阈值更新方法选择。

常用的阈值筛选方法有3种：硬阈值法、软阈值法和半软阈值法。Starck等［15］经过实验验证采用硬阈值法能得到较好的信号分离结果。

硬阈值筛选的判断准则为

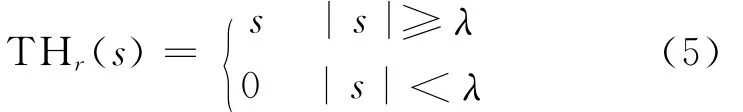
其中：λ为阈值。

在原MCA算法中，阈值的更新方法为线性递减，即随着迭代次数的增加，阈值不断线性递减，即

其中：δ1为初始阈值；δmin为最小阈值；Lmax为最大迭代次数。

虽然阈值的线性递减具有算法简单的优点，但无法估算成功分离信号所需要的最少迭代次数，迭代次数设置得太小，导致信号分离失败，太大导致MCA算法计算量过大。Bobin等［16］提出了一种基于最大均值（mean of max，简称MOM）的阈值更新策略，改善了MCA算法的性能，提高了MCA方法的收敛速度。

假设信号s为K 个不同形态的分量｛s1，s2，…，sK｝的线性组合，MCA算法可归纳为求解如下优化问题

其中：σ为信号噪声方差。

基于MOM的阈值更新计算公式为

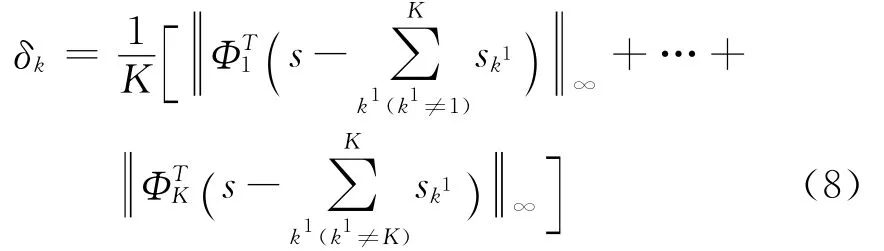
在每次迭代过程中，MOM阈值更新策略充分考虑到剩余量rk的变化，并重新计算阈值δk；因此，MOM阈值更新策略提供了一种自适应阈值更新方法。阈值的线性递减更新方法与信号分解系数无关。Bobin等［16］通过信号仿真说明：在每次迭代过程中，根据MOM阈值更新策略，由信号的当前剩余量rk重新计算新的阈值δk，因而能更快地计算出信号的分解系数αk，线性递减法中信号的分解系数大部分是在最后一次迭代中才能计算出来。

综合以上分析，在本研究中阈值筛选方法采用硬阈值法，阈值更新方法采用MOM策略，即基于TH－MOM的MCA算法。

1.4 形态分量分析的字典选择

在信号稀疏分解中，将参数化的波形函数称为字典。在数学上，字典Φ为参数化波形函数φγ的集合，即

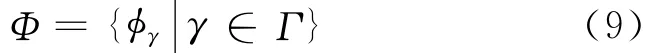
其中：γ为波形函数的参数；Γ为参数集合。

若字典Φ中元素的数量等于信号的长度n，则称字典是完备的。若字典Φ中元素的数量大于信号的长度n，则称字典是过完备的。在信号稀疏分解中一般选用过完备字典。

为了匹配被分析信号的结构特征，需要根据信号的结构特征设计和选择字典。字典不仅要匹配被分析信号的特征结构要求，而且要保证信号分解和重构算法可以实现。目前，常用的字典有Dirac字典、Fourier字典、小波字典和小波包字典等。

2 信号仿真分析

为了验证形态分量分析能有效分离形态各异信号的优良特性，给出由脉冲信号加噪声、频率分别为20Hz，45Hz的正弦信号加噪声组成的复合仿真信号，信噪比为5dB。采样频率为2kHz，采样时间为0.256s，采样点数为512。仿真信号的时域图形如图1所示。随机选取混合矩阵A为

将图1（a），（b）和（c）所示的3个仿真信号线性混合，得到4个混合信号如图2所示。

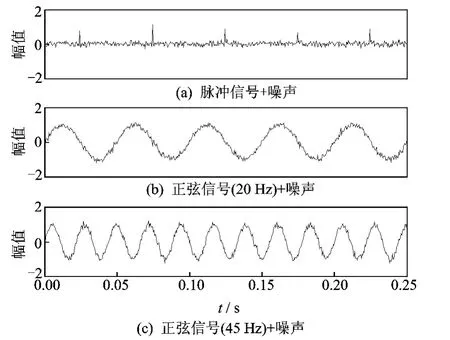
图1 仿真信号

图2 混合后仿真信号

选取过完备的Dirac字典、Fourier字典构成复合字典，分别用来匹配仿真信号中的脉冲冲击和正弦信号。采用MCA算法对仿真信号进行分离，结果如图3所示。可以看出，基于形态分量分析的信号分析技术由于充分利用了信号成分的形态多样性和稀疏性的特点，将脉冲信号与2个频率不同的正弦信号的混合信号进行了有效分离，并有效去除原信号中的噪声。

图4为图1的仿真信号采用固定点（FastICA）算法进行独立分量分析的结果。对比图4和图3可以看出，独立分量分析虽然能将3个不同形态的信号分离，但其降噪效果较差，分离后信号的信噪比较低。形态分量分析不仅能将3个形态各异的信号进行有效分离，而且能有效去除信号中噪声的影响，提高了分析信号的信噪比。

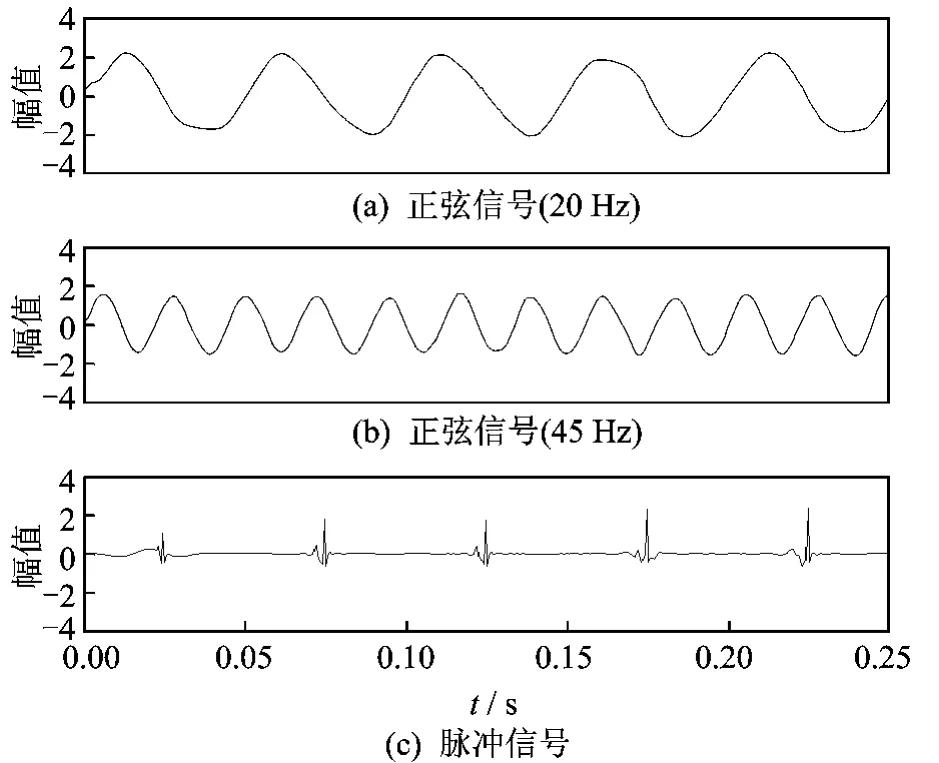
图3 MCA分离后的信号

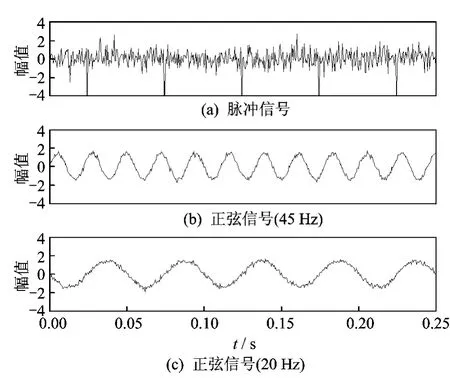
图4 FastICA分离后的信号

3 基于形态分量分析的齿轮箱复合故障诊断

齿轮箱振动信号采集系统可参考文献［25］，齿轮箱输入轴齿轮齿数z1＝30，输出轴齿轮齿数z2＝50，模数m＝2.5，输入轴转速为1.5kr／min，齿轮箱运行时的一阶啮合频率fm＝750Hz。实验中齿轮箱输入轴的轴承型号为滚珠轴承208，采用线切割技术分别在输入轴滚珠轴承的内圈和外圈加工深为1mm、宽为0.5mm的沟槽，分别模拟轴承内圈、外圈局部裂纹故障。将轴承滚珠沿切掉0.5mm模拟滚珠故障。将齿轮箱输入轴齿轮单个齿面用锉刀锉掉0.4mm厚金属，模拟齿轮单齿磨损故障。分别在齿轮箱输入轴、输出轴两端轴承上方安装传感器，测量4通道振动信号。

轴承内圈故障特征频率为

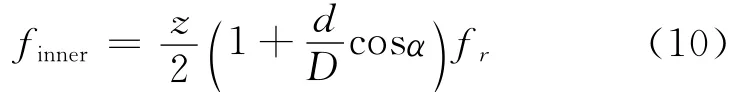
轴承外圈故障特征频率为

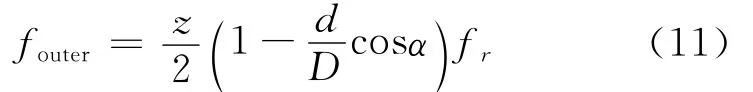
轴承滚珠故障特征频率为

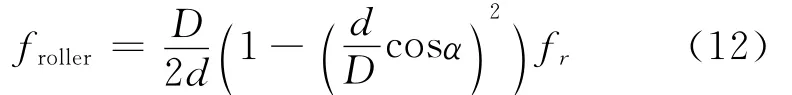
其中：fr为轴承内圈（输入轴）的旋转频率；D为轴承中径；d为滚动体直径；z为滚动体的个数；α为轴承负载的接触角［25］。

实验时采样频率为4 096Hz，采样点数为2 048。根据208轴承的几何尺寸，滚动体的个数z＝10，d＝18.333mm，D＝97.5mm，轴承负载的接触角α＝0°。将上述参数带入式（10）～（12），得到finner＝148.5Hz，fouter＝101.5Hz，froller＝54.1Hz。

图5为输入轴齿轮、轴承内圈、外圈和滚珠存在复合故障时，由4个传感器采集得到的4通道振动信号。从图5看出，当输入轴齿轮齿面磨损、滚动轴承内圈、外圈和滚珠存在故障时，其时域振动信号产生了峰值较高的高频冲击振动；但由于受强背景噪声和诸多信号混叠的影响，只根据时域振动信号难以确定齿轮箱中故障发生的位置和提取故障特征。

图6分别为齿轮箱存在多种复合故障时，4个传感器采集得到的振动信号的快速傅里叶变换。可以看出，由于采集信号的几个故障特征频率在每一个频谱图上相互混叠，且又有强噪声的影响，仅对采集得到的时域信号简单进行快速傅里叶变换，难以确定故障发生的部位和类型。

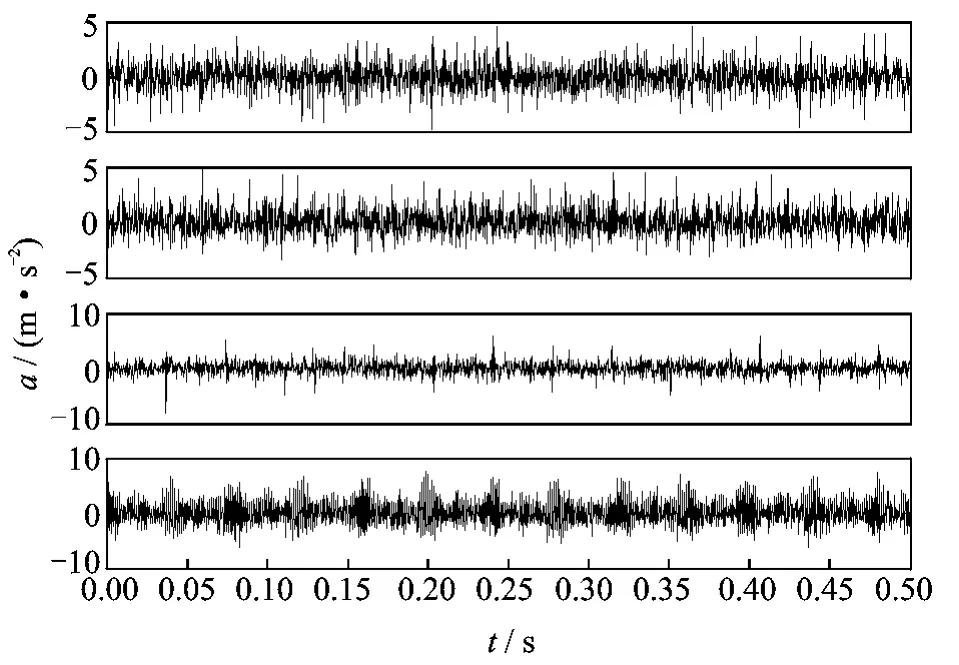
图5 齿轮箱存在复合故障的时域振动信号

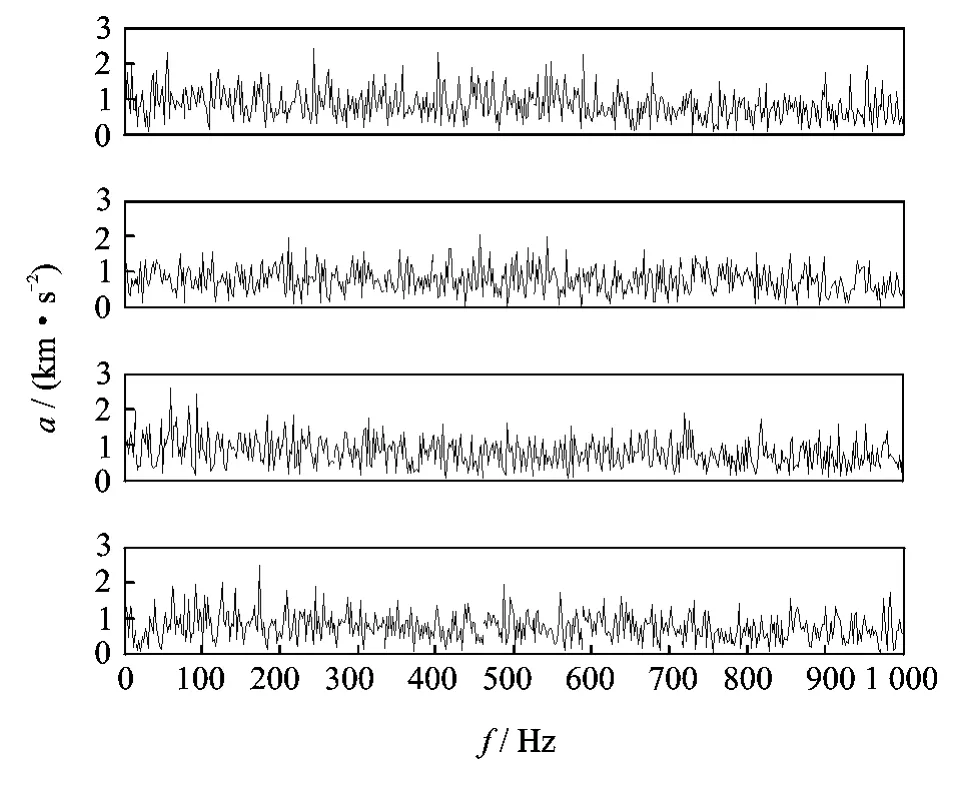
图6 齿轮箱复合故障时域振动信号的FFT

由于齿轮箱故障振动信号包含有瞬态冲击、简谐振动和背景噪声等，因此为了匹配被分析信号的特征结构，在进行形态分量分析时采用过完备复合字典。构造Fourier字典、Dirac字典和8阶消失矩Symlet小波字典，分别用以匹配齿轮箱振动信号中的简谐振动、瞬态冲击和其他瞬态振动现象，采用MCA算法对采集的4通道振动信号进行形态分量分析。图7为分离出的4通道源信号的时域图。图7（a）对应轴承外圈故障信号，且周期性脉冲峰值的间隔也等于轴承外圈特征故障周期（0.009 852s）。图7（b）对应轴承内圈故障信号，且脉冲幅值线的间隔等于轴承内圈特征故障周期（0.006 73s）。图7（c）对应轴承滚珠故障信号，可以看出明显的周期性冲击的幅值线，且周期性脉冲峰值的间隔等于轴承滚珠特征故障周期（0.018 48s）。图7（d）对应齿轮磨损故障信号，且脉冲幅值线的间隔等于输入轴的转动周期（0.04s）。可见，形态分量分析的结果在时域内验证了MCA方法的有效性。

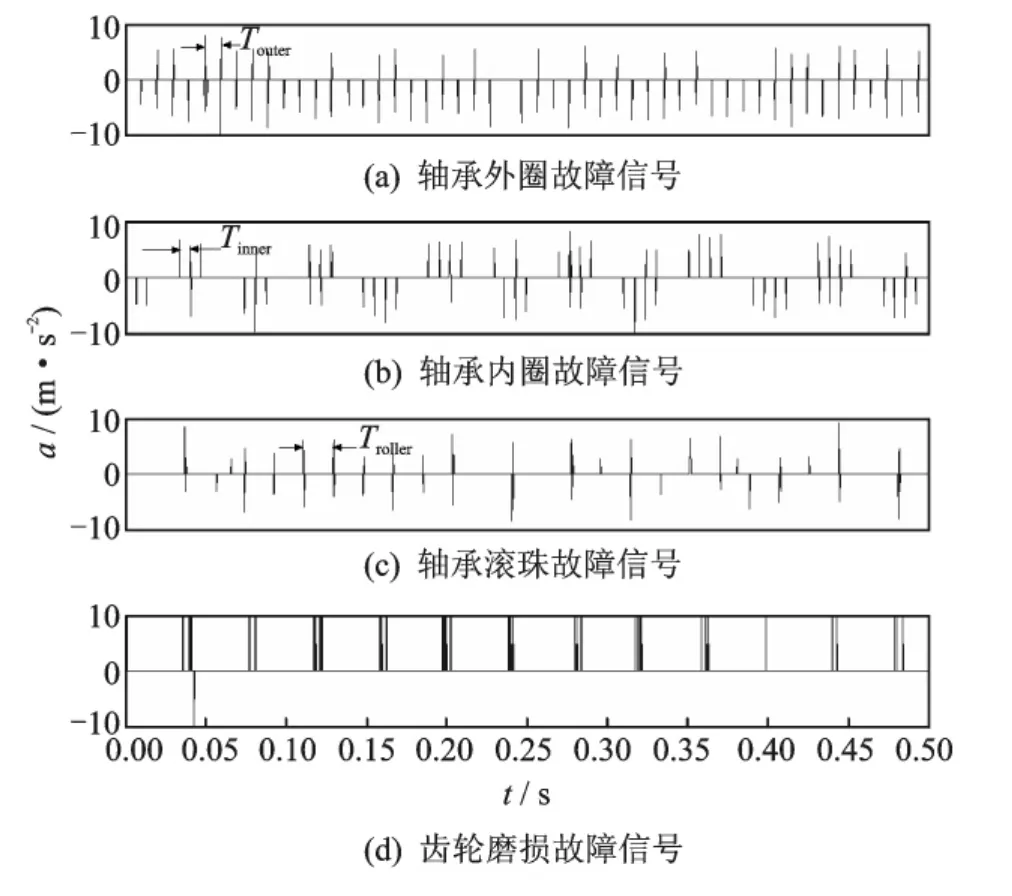
图7 MCA分解信号

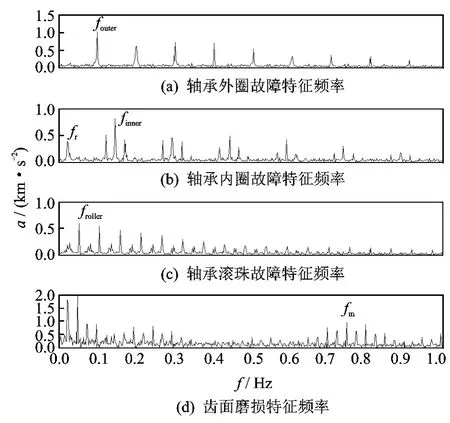
图8 MCA分解信号的快速傅里叶变换

当轴承内圈存在局部故障点时，随着轴承内圈旋转，分布到故障点的静态载荷密度随内圈的旋转而周期性的变化。在频谱图中，表现为在轴承内圈的转动频率fr、特征故障频率finner及其高倍频处有明显的谱线，且在频率为finner及其高倍频处存在以fr为间隔的边频带。轴承外圈故障在频域内表现为以外圈故障特征频率fouter为重复频率且按指数规律衰减的高频共振序列。轴承滚珠故障在频域表现为以滚珠故障特征频率froller为重复频率且按指数规律衰减的高频共振序列。图8为图7中各形态分量的快速傅里叶变换，可以看到：图8（a）中轴承外圈故障特征频率fouter及其高倍频处存在明显的峰值；图8（b）中轴承内圈故障特征频率finner及其高倍频处也存在明显的峰值线，且在频率为finner及其高倍频处存在以fr为间隔的边频带；图8（c）中轴承滚珠故障特征频率froller及其高倍频也非常明显；图8（d）中，在低频段存在输入轴的转动频率fr及其倍频，在高频段存在以齿轮第1阶啮合频率fm及以fr为间隔的边频带，这与输入轴齿面磨损的故障特征一致。图8的实验结果与理论分析相符，在频域内验证了提出方法的正确性和有效性。

为了验证形态分量分析在齿轮箱复合故障诊断中的有效性和准确性，采用独立分量分析对图5给出的振动信号进行了分析。图9为采用FastICA算法分离出的4个源信号的时域图形。图9的时域分离信号由于受噪声的影响，直观上难以区分4个源信号分别对应的故障。图10为FastICA分解后信号的快速傅里叶变换。可以看出，4个分离信号分别对应轴承的滚珠、外圈、内圈和齿轮磨损故障，在频谱图中，虽能找出各自的故障特征频率，但由于受噪声影响，故障特征不太明显。

图11为采用批数据处理独立分量分析JADE算法［26］分离出的4个信号的时域图形。从图11的时域分离信号直观上难以区分4个分离信号分别对应齿轮箱的故障。图12为JADE算法分解后信号的快速傅里叶变换。可以看出，4个分离信号分别对应齿轮齿面磨损、轴承的内圈、滚珠、外圈故障。在频谱图中虽能找出各自的故障特征频率，但由于受噪声影响，故障特征也不太明显。

对比图7、图9、图11和图8、图10、图12可以得出：采用笔者提出的形态分量方法不仅能将齿轮箱的复合故障信号进行有效分离，而且也提高了信号的信噪比和瞬态冲击的检测能力，从而提高了齿轮箱复合故障诊断的准确性和有效性。

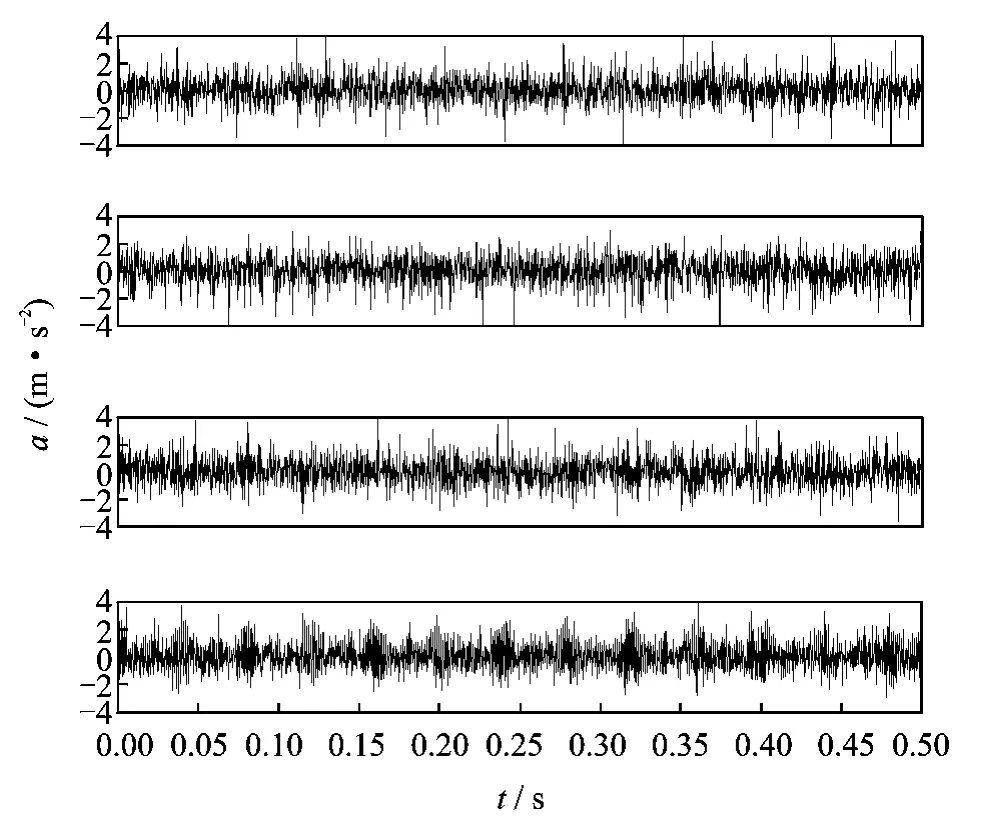
图9 FastICA分解信号的时域波形

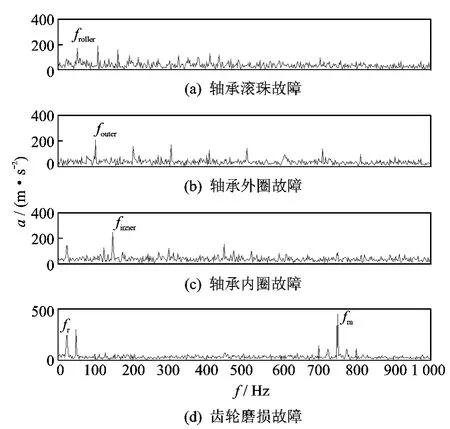
图10 FastICA分解信号的快速傅里叶变换

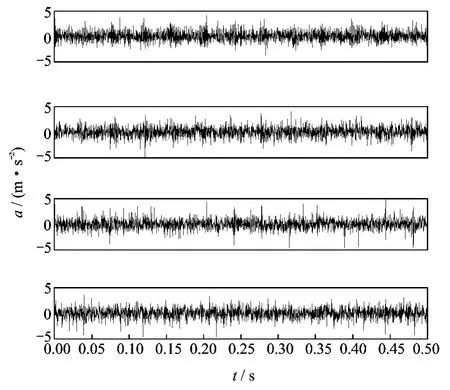
图11 采用JADE方法分解信号

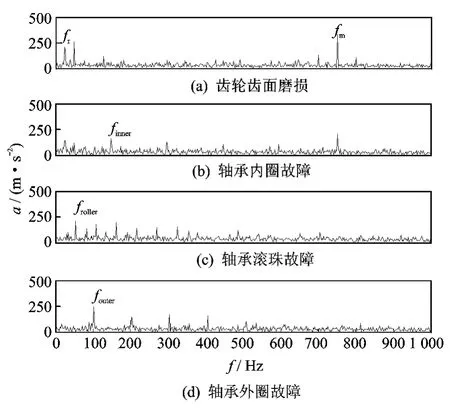
图12 采用JADE方法分解信号的FFT

4 结束语

形态分量分析充分利用了信号的形态多样性和稀疏性的特点，把信号源看作是不同形态分量的线性组合，利用稀疏性估计源信号和混合矩阵，在将源信号分离的同时，能有效降低噪声的影响，MCA是一种快速有效的盲源分离方法。通过仿真信号和齿轮箱轴承内圈、外圈、滚珠和齿面磨损复合故障振动信号的分析表明，本研究方法不仅能将不同故障的源信号进行有效分离，提高了信号信噪比，而且有效提取了齿轮箱的微弱故障特征，其性能优于传统的独立分量分析方法。

［1］ Staszewski W J，Worden K，Tomlinson G R.The frequency analysis in gearbox fault detection using the Wigner－Ville distribution and pattern recognition［J］.Mechanical Systems and Signal Processing，1997，11（5）：673－692.

［2］ Li Hui，Zhang Yuping，Zheng Haiqi.Application of Hermitian wavelet to crack fault detection in gearbox［J］.Mechanical Systems and Signal Processing，2011，25（4）：1353－1363.

［3］ Cheng Junsheng，Yu Dejie，Yang Yu.Application of an impulse response wavelet to fault diagnosis of rolling bearings［J］.Mechanical Systems and Signal Processing，2007，21（2）：920－929.

［4］ 于德介，程军圣，杨宇.Hilbert－Huang变换在滚动轴承故障诊断中的应用［J］.中国机械工程，2003，14（24）：2140－2142.Yu Dejie，Cheng Junsheng，Yang Yu.Application of the Hilbert－Huang transform method to roller bearing fault diagnosis［J］.China Mechanical Engineering，2003，14（24）：2140－2142.（in Chinese）

［5］ Li Hui，Zheng Haiqi，Tang Liwei.Faults monitoring and diagnosis of ball bearing based on Hilbert－Huang Transformation［J］.Key Engineering Material，2005，291－292：649－654.

［6］ Li Hui，Zheng Haiqi，Tang Liwei.Bearing fault detection and diagnosis based on Teager－Huang transform［J］.International Journal of Wavelets，Multiresolution and Information Processing，2009，7（5）：643－663.

［7］ Chen S S，Donoho D，Saunders M.Atomic decomposition by basis pursuit［J］.SIAM Journal on Scientific Computing，1999，20（1）：33－61.

［8］ Chen S.Basis pursuit［D］.Stanford，CA：Department of Statistics，Stanford University，1995.

［9］ Mallat S，Zhang Z F.Matching pursuit with time frequency dictionaries ［J］.IEEE Transactions on Signal Processing，1993，41（12）：3397－3415.

［10］Yang H Y，Mathew J，Ma L.Fault diagnosis of rolling element bearings using basis pursuit［J］.Mechanical Systems and Signal Processing，2005，19（2）：341－356.

［11］Hyv¨arinen A，Karhunen J，Oja E.Independent component analysis［M］.［S.l.］：John Wiley ＆ Sons，Inc.，2001：1－100.

［12］Feng Z P，Chu F L.Application of atomic decomposition to gear damage detection［J］.Journal of Sound and Vibration，2007，302（1－2）：138－151.

［13］苏永振，袁慎芳.基于独立分量分析的多源冲击定位方法［J］.振动与冲击，2009，28（8）：134－137，157.Su Yongzhen，Yuan Shenfang.Method for locating multiple impact sources based on independent component analysis［J］.Journal of Vibration and Shock，2009，28（8）：134－137，157.（in Chinese）

［14］刘婷婷，任兴民.独立分量分析在机械振动信号分离中的应用［J］.振动、测试与诊断，2009，29（1）：36－41.Liu Tingting，Ren Xingmin.Application of independent component analysis to vibration signal separation of rotational machine［J］.Journal of Vibration，Measurement ＆ Diagnosis，2009，29（1）：36－41.（in Chinese）

［15］Starck J L，Moudden Y，Robin J.Morphological component analysis［C］∥Processings of SPIE.San Diego，California：［s.n.］，2005，5914：1－15.

［16］Bobin J，Starck J L，Fadili J.Morphological component analysis：an adaptive thresholding strategy［J］.IEEE Transactions on Image Processing，2007，16（11）：2675－2681.

［17］Bobin J，Moudden Y，Starck J L.Enhanced Source Separation by Morphological Component Analysis［C］∥IEEE International Conference on Acoustics Speech and Signal Processing Proceedings.Toulouse，France：［s.n.］，2006：833－836.

［18］Starck J L，Elad M，Donoho D.Redundant multiscale transforms and their application for morphological component separation［J］.Advances in Imaging and E－lectron Physics，2004，132（82）：287－348.

［19］李映，张艳宁，许星.基于信号稀疏表示的形态成分分析：进展和展望［J］.电子学报，2009，37（1）：146－152.Li Ying，Zhang Yanning，Xu Xing.Advances and perspective on morphological component analysis based on sparse representation［J］.Acta Electronica Sinica，2009，37（1）：146－152.（in Chinese）

［20］耿瑞敏，练秋生，孙马秋.基于形态学成分分析的指纹分离［J］.计算机工程与应用，2008，44（16）：188－190.Geng Ruimin，Lian Qiusheng，Sun Maqiu.Fingerprint separation based on morphological component analysis［J］.Computer Engineering and Applications，2008，44（16）：188－190.（in Chinese）

［21］张涛，洪文学.基于自适应字典选择的MCA图像修复方法［J］.光学技术，2010，36（5）：672－677.Zhang Tao，Hong Wenxue.Image inpainting based on MCA featured adaptive dictionary selection［J］.Optical Technique，2010，36（5）：672－677.（in Chinese）

［22］付蓉，李洁，高新波.基于形态学成分分析的静态极光图像分类算法［J］.光子学报，2010，39（6）：1034－1040.Fu Rong，Li Jie，Gao Xinbo.Static aurora images classification based on morphological component analysis［J］.Acta Photonica Sinica，2010，39（6）：1034－1040.（in Chinese）

［23］Yong Xinyi，Ward R K，Birch G E.Generalized morphological component analysis for EEG source separation and artifact removal［C］∥Proceedings of the 4th International IEEE EMBS Conference on Neural Engineering Antalya.Turkey：［s.n.］，2009：343－347.

［24］Sardy S，Bruce A G，Tseng P.Block coordinate relaxation methods for nonparametric signal denoising with wavelet dictionaries［J］.Journal of Computational and Graphical Statististics，2000，9（2）：361－379.

［25］Li Hui，Zhang Yuping，Zheng Haiqi.Hilbert－Huang transform and marginal spectrum for detection and diagnosis of localized defects in roller bearings［J］.Journal of Mechanical Science and Technology，2009，23（2）：291－301.

［26］Cardoso J F.Blind signal separation：statistical principles［J］.Proceedings of The IEEE，1998，9（10）：2009－2025.