基于非平稳信息的转子瞬态动平衡方法*

温广瑞，臧廷朋，廖与禾

（西安交通大学机械制造系统国家重点实验室 西安，710049）

引 言

旋转机械的起停车过程是机组运行中的一个重要阶段，控制升降速过程中的临界振动幅值成为保障机组安全平稳运行的重要手段。在工业现场中，降低临界共振幅值的基本方法是使转子系统以较大的角加速度通过临界共振区，但该方法由于受到驱动系统的限制而不能取得理想的效果。国内外学者对如何降低转子过临界的共振幅值进行了相关研究。K.T.Millsaps等［1］通过研究不同加速度的幅值－转速特性，提出了一种“加速度调制”的方法，该方法通过控制起车过程中不同阶段的加速度大小来降低临界共振幅值。文献［2］通过研究转子起车过程中振动幅值和相位之间的关系，提出了“相位调制”的方法来降低转子临界共振幅值。上述方法都是通过控制的思想来降低临界共振幅值，由于转子系统的复杂性，因而在实际应用中受到很大限制。动平衡是降低 转子振动的有效方法［3－4］，目前使用的转子现场动平衡方法包括影响系数法和模态平衡法，都是以能够获得转子系统的稳态响应为基础，通过平衡转速下试重前、后的稳态响应来确定校正质量。在实际的平衡过程中，多次获取临界转速附近的稳态响应不但降低了平衡效率，同时由于转子在临界转速附近的振动较大，还可能给转子系统带来较大危害；因此，若能通过转子起车过程中的不平衡加速响应信息实现转子的平衡，将对降低转子系统的临界振动幅值产生指导意义。

转子的起停车过程不平衡响应是一个调幅调频信号，具有很强的瞬变性，选择适当的信号处理方法提取所需的振动信息就显得尤为重要。笔者采用经验模态分解提取升速过程的转频模态，运用键相信号获得转子系统的初相点和转速信息，研究利用全息动平衡方法［5］实现转子系统的瞬态动平衡。

1 经验模态分解

EMD根据信号的局部特征时间尺度把信号分解为一组有限数量的固有模态函数（intrinsic mode function，简称IMF）。其具体分解步骤［6－7］如下：

1）分别采用三次样条曲线拟合原始信号X（t）的极大值点和极小值点，得到上、下包络线，取上、下包络线的均值序列为m（t）；

2）计算原始信号与上、下包络线均值m（t）的差值h1（t）＝X（t）－m（t）；

3）判断h1（t）是否满足固有模态函数的两个限定条件，若不满足则重复步骤1和2，直至得到第1个IMF：c1（t）＝h1（t）；

4）从原始信号中减去c1（t），得到剩余序列值r1（t）＝x（t）－c1（t）；

5）把r1（t）作为待分解信号，重复以上步骤直至满足分解停止准则，经过EMD分解原始信号被分解为若干个IMF和一个余项rn（t）的和

EMD是一种自适应的信号时频分析方法，该方法根据信号自身的局部特征时间尺度把信号分解为一系列固有模态函数。每个IMF代表了信号的不同尺度特征，通过对分解得到的各个IMF分析可以准确把握原信号中的局部特征和整体特征。

2 基于非平稳信息的转子瞬态动平衡

2.1 零相移低通滤波

零相移低通滤波能够保证信号的原始相位信息不发生变化，同时降低信号中的高频成分和噪声干扰，提高EMD分解的效率和精度。设原始信号序列为x（i），i＝0，1，…，n，其时域逆转信号序列为y（i）＝x（n－i），i＝0，1，…，n。把x（i），y（i）延拓至整个时间轴，根据双边Z变换可得

根据时域逆转前、后信号序列Z变换的关系，构造如图1所示的零相移低通滤波器原理图，其中H（z）为普通低通滤波器的传递函数。

图1 零相移低通滤波原理图

由式（2）和图1可得

令z＝ejw，带入式（3）得

由式（4）可知，输出信号序列频谱等于输入信号序列频谱乘以一个实数，两者具有完全相同的相位信息，从而实现零相移低通滤波。

2.2 转频模态分量的提取

对原始起车振动信号序列进行保相低通滤波，设置滤波器的截止频率高于转子起车过程的最高转频。根据EMD的自适应滤波特性，EMD可以看成是一组自适应的高通滤波器，它的截止频率和带宽都随着信号和分解过程的变化而变化，分解得到一组频率成分从高到底的IMF。基于以上两点可以判定EMD分解的第1个固有模态函数即为转频模态分量。图2为某次起车过程信号EMD分解结果，其中固有模态函数c1即为转频模态分量。

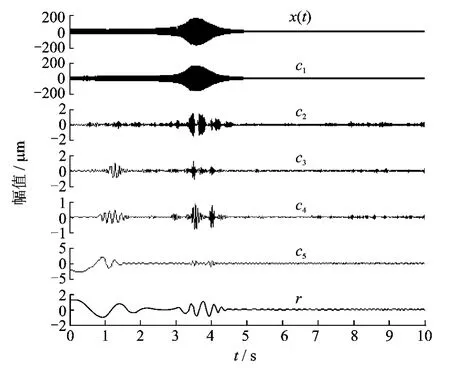
图2 转频模态分量提取

2.3 基于等转速的信号截取

从图2可知，利用EMD从起车振动信号中提取的转频模态分量仍然是一个调幅、调频的非平稳信号，应用传统傅里叶变换的方式获取所需的幅值、相位信息是不合理的。对于有相同时间历程的键相信号和振动信号，任何两个相邻的键相脉冲可以确定相应的转速，利用相邻的键相脉冲去截取同一个升速过程中对应的振动信号，可以得到这种转速下对应的时域波形［8－9］。从时域波形中可以得到键相传感器对准键相槽时同一截面两个方向振动信号的幅值信息，获得初相点为

根据初相矢公式和基于等转速的信号截取方法获得平衡转速下的初相点信息，通过添加试重，利用全息动平衡方法实现转子的动平衡［10］。

3 平衡实验

在Bently RK4转子实验台上对本研究提出的平衡方法进行验证。为了充分考虑转子支撑各向异性的影响，分别在A，B两测量面上安装相互垂直的电涡流传感器，实验台结构和传感器的安装方式如图3所示。设置采样频率为2 048Hz，采样时长为80s，选择合适的升速比，测量得到转子系统在0～4kr／min范围内的瞬态加速响应如图4所示。由图可知，转子系统一阶共振峰值超过200um，而在其他转速处振动幅值较小，因此首先只考虑对转子的一阶不平衡进行校正。

图3 传感器安装示意图

图4 转子系统在0～4kr／min内的加速瞬态响应

利用转频模态分量的提取方法和基于等转速的信号截取方式对各个通道起车加速响应进行处理，得到原始状态下A，B两截面初相点信息随转速的变化曲线，如图5所示。

图5 原始振动初相点信息随转速的变化曲线

在左右两个校正平面A，B添加0.8g＜90°的试重，保持采样参数和升速比不变，再次起车测量A，B两截面的瞬态加速响应。利用EMD分解提取试重后的转频模态，采用基于等转速的截取方法分别截取原始起车瞬态响应和试重后起车瞬态响应的转频模态，把对应转速下的时域波形相减并按照初相点的合成方式进行合成，得到纯试重初相点信息随转速的变化曲线，如图6所示。

为了避免一阶临界转速前、后相位变化剧烈带来的误差，应选择80%～90%一阶临界转速附近的振动信息进行平衡。转子的一阶临界转速为2.1kr／min左右，选取平衡转速为1.9kr／min，平衡转速下的配重计算数据如表1所示。

表1 1.9kr／min时配重计算数据表

由于受到配重质量和加重角度的限制，实际两个截面的配重量均为0.6g＜90°。平衡前、后各个通道的临界振动幅值及平衡效果如表2所示。

表2 平衡效果

可以看出，平衡后转子各个通道的临界振动幅值都有较大幅度的降低。截面A振动幅值分别由平衡前的206μm，164.2μm 减小到52.47μm，33.36μm。截面B的振动幅值分别由平衡前的195.2μm，147.1μm减小到58.39μm，50.5μm，最大降低幅度达到79.68%。均方振动幅值也有明显的下降，由平衡前的179.68μm减小到49.56μm，下降幅度为72.42%，减振效果明显。

添加配重后，求原始状态和平衡后起车加速瞬态响应转频模态的Hilbert包络，并和相应的转速对应，得到平衡前、后各个通道的转频幅值伯德图，如图7所示。可见，临界振动幅值有明显的降低。

图6 纯试重初相点信息随转速的变化曲线

图7 平衡前、后转频幅值伯德图

4 结束语

利用非平稳信息对转子系统动平衡进行探索，提出了基于非平稳信息的转子瞬态动平衡方法，实现了转子系统的一阶模态平衡，并进行了实验验证。和传统平衡方法相比，提出的动平衡方法有以下优点：a.测量速度快，只需要转子系统起车的瞬态响应数据，不需要稳态测量；b.平衡效率高，充分继承了全息动平衡效率高的优点，只需一次试重即可实现两个截面的同时平衡；c.平衡风险低，传统的模态平衡法需要在临界转速附近停留以获得稳态响应，而本研究方法只需要起车加速瞬态响应，降低了平衡风险。

［1］ Millsaps K T，Reed G L.Reducing lateral vibrations of a rotor passing through critical speeds by acceleration scheduling［J］.ASME Journal of Engineering for Gas Turbines and Power，1998，120（3）：615－620.

［2］ Wang S M，Lu Q S，Twizell E H.Reducing lateral vibration of a rotor passing through critical speed by phase modulating［J］.ASME Journal of Engineering for Gas Turbines and Power，2003，125（3）：766－771.

［3］ Chen Xuqin，Jia Yujing，Cheng Guangzhen.Research on field balancing of rotor［J］.Applied Mechanics and Materials，2012，201：83－86.

［4］ Poornima V D，Adinarayana S，Rao B V A.Two plane balancing of a conical rotor driven by vertical belt system designed to reduce gyro effect［J］.International Journal of Mechanical Engineering and Robotics Research，2012，1（3）：1－8.

［5］ 屈梁生，邱海，徐光华.全息动平衡技术：原理与实践［J］.中国机械工程，1998，9（1）：60－63.Qu Liangsheng，Qiu Hai，Xu Guanghua.Rotor balancing based on holospectrum analysis：principle and practice［J］.China Mechanical Engineering，1998，9（1）：60－63.（in Chinese）

［6］ Huang N E，Shen Z，Long S R.The empirical mode decomposition and Hilbert spectrum for nonlinear and non－stationary time series analysis［J］.Proceeding of Royal Society London A，1998，454：903－995.

［7］ 盖广洪.转子启动信号处理中的低频分量提取研究［J］.振动、测试与诊断，2005，25（2）：91－94.Gai Guanghong.The processing of rotor startup signals based on empirical mode decomposition［J］.Journal of Vibration，Measurement ＆ Diagnosis，2005，25（2）：91－94.（in Chinese）

［8］ 廖与禾，郎根峰，屈梁生.平衡目标选择与全息动平衡法的改进研究［J］.热能动力工程，2008，23（4）：382－386.Liao Yuhe，Lang Genfeng，Qu Liangsheng.A study on the improvement of balancing target selection and holographic dynamic balancing method［J］.Journal of Engineering for Thermal Energy and Power，2008，23（4）：382－386.（in Chinese）

［9］ 刘石，屈梁生.全息谱技术在现场动平衡前故障诊断中的应用［J］.振动、测试与诊断，2004，24（2）：270－274.Liu Shi，Qu Liangsheng.Fault diagnosis prior the field balancing based on holospectrum［J］.Journal of Vibration，Measurement ＆ Diagnosis，2004，24（4）：200－274.（in Chinese）

［10］Huang Jinping，Ren Xingmin，Deng Wangqun，et al.Two－plane balancing of flexible rotor based on accelerating unbalancing response data［J］.Acta Aeronautica Et Astronautica Sinica，2010，31（2）：400－409.