简支形状记忆合金层合梁的混沌及安全盆侵蚀*

葛 根，竺致文，许 佳

（1.天津工业大学机械工程学院 天津，300387）（2.天津大学机械学院 天津，300072）

引 言

形状记忆合金梁的振动具有丰富的非线性动力学特性，研究其振动特性对研究形状记忆合金的工程应用具有重要的实用价值。国内外学者提出了众多关于形状记忆合金梁振动的研究成果。Collet等［1］考虑了形状记忆合金在拉、压、温度载荷中的对称性假设后，研究了形状记忆合金梁的动力学行为。Hashemi等［2］研究了在拉、压、温度加载中的非对称性假设下梁的自由振动和脉冲激励振动问题。文献［3］用数值方法研究了形状记忆合金双杆系统的同宿分岔和混沌现象。张清泉等［4－5］根据 Machado本构模型建立了形状记忆合金梁的动力学模型，并研究了其振动的稳定性和混沌现象。吴志强等［6］研究了形状记忆合金层合梁的非线性动力响应特性。葛根等［7］研究了简支形状记忆合金梁受简谐和随机共同激励下的混沌阈值问题。王征等［8］研究了形状记忆合金的成振作用。

笔者基于vanderpol环模型模拟了形状记忆合金本构模型中的迟滞环特性，从该模型出发建立了受轴向激励的形状记忆合金简支层合梁的振动模型。用待定固有频率法研究了该模型的非线性参数对系统固有频率的影响，结合计算结果和时间尺度变换表示了该系统改进后的Melnikov函数，得出较精确的系统发生混沌的阈值。采用数值方法得到了系统安全域边界的侵蚀现象，发现激励幅值的变化导致安全盆边界出现分形结构，这是识别混沌的另一种有效而可靠的方法。这些结果对形状记忆合金梁的应用安全具有较大的实际意义。

1 形状记忆合金层合梁的振动模型

考虑一个矩形截面的简支Euler－Bernoulli形状记忆合金层合梁如图1所示。梁长为l，b为横截面宽度，H为梁高。中间层是高度为h的均质线弹性材料基底层，上下为等厚度的形状记忆合金层，层厚度为（H－h）／2。层间牢固粘结，梁轴线中点的y方向位移为w。轴向受简谐激励N，形式为N＝p0＋pcos（Ωt）。因为形状记忆合金满足拉压条件下的应力应变关系的对称性［1］，故坐标中心可选为梁横截面的几何中心处。

假设该梁为小挠度梁，其动力学方程为

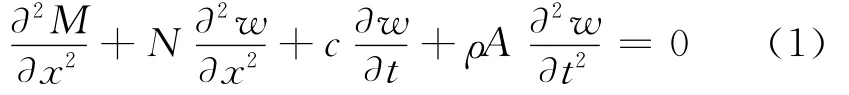
其中：c为线性阻尼；ρ为梁的平均密度；A为梁的横截面积；M为梁的弯矩；w为中点横向位移。该两端简支梁的边界条件可表示为

图1 简支形状记忆合金梁的模型及坐标

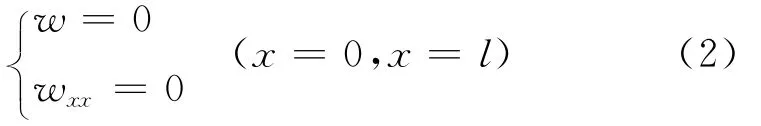
满足振动边界条件的伽辽金一阶截断为

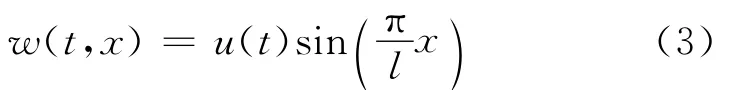
考虑小挠度梁满足平面假设，其几何变形条件为

梁横截面上弯矩为正应力σ对中性轴的力矩在横截面上的积分

梁横截面的正应力分布如图2所示。显然，线弹性基底的应力应变关系满足最基本的胡克定律σ＝Eε，E为弹性模量。形状记忆合金应力应变关系为复杂的非线性关系。根据文献［7］中的等应变加、卸载实验数据可知，在不考虑温度变化时，形状记忆合金的加载－卸载应力应变曲线有明显的滞后环特性，如图3所示。

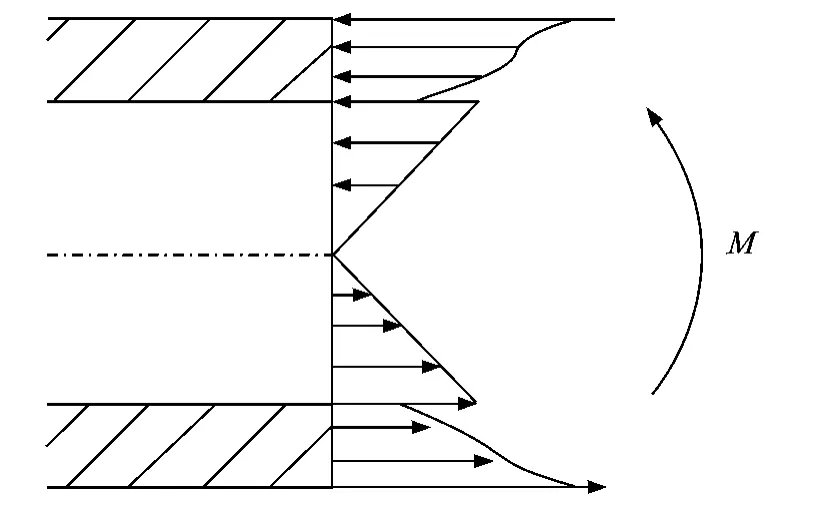
图2 形状记忆合金梁横截面正应力分布

图3 形状记忆合金的应力应变关系

Falk曾建立了一个平滑的多项式模型来模拟该应力应变关系［4］

其中：T 为温度；TM为马氏体临界温 度；a1，a2，a3为常数。

显然，该模型不足以模拟滞后环特性。为模拟这一特性并使函数形状光滑以利于后续分析，可考虑建立一个关于原点对称的vanderpol环加上一条骨架曲线形式的模型。

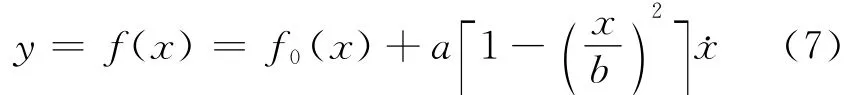
其中：f0（x）为迟滞环的骨架曲线；参数a，b为骨架曲线和实验应力应变曲线之间的偏差。

假设应力 －应变环的对称中心为G （ε0，σ0），则形状记忆合金的应力－应变关系可表示为

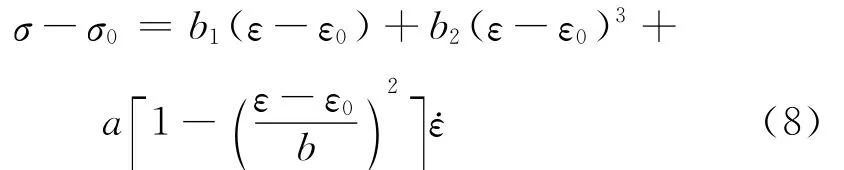
展开为

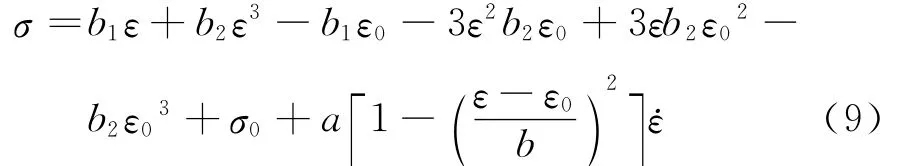
考虑到当ε＝0时，加载和卸载曲线的对应应力值必需相等，且此时形状记忆合金应没有残余应力，故模型参数应满足由此可得形状记忆合金的应力应变最终函数关系为

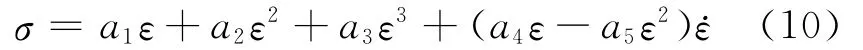
以上参数需要根据实际的形状记忆合金试件的实测数据来确定。当温度不变时，与式（6）比较可知，本研究模型为一个迟滞环表达式，Falk模型仅相当于本研究模型式（10）得的骨架曲线。

把式（3），（4）代入式（10），得到应力和位移 w的关系，再代入式（5）得到弯矩表达式为

其中：M1，M2分别为上、下两层形状记忆合金层形成的弯矩；M3为中间层上的弯矩。

化简得

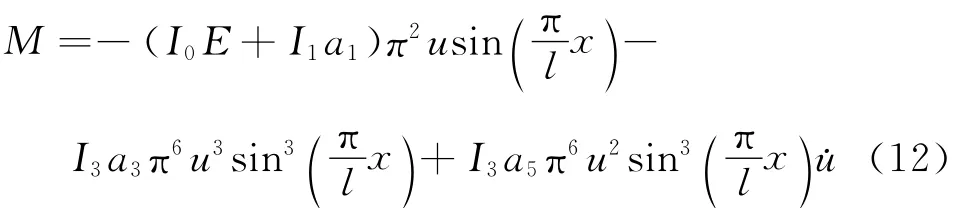
把式（3），（12）代入式（1），积分可得单自由度常微分形式的梁动力学非线性振动方程为

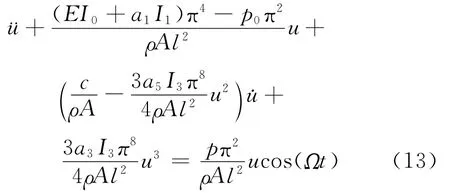
从式（13）发现，由于形状记忆合金层的作用，使梁的振动方程中出现了非线性阻尼及刚度项。为了便于后续的非线性分析和揭示系统可能存在的动力学现象，对式（11）作无量纲变化，并略去上标

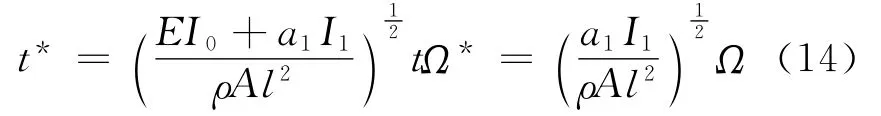
模型（13）可变形为以下无量纲形式

考虑静态载荷p0大于极限屈曲载荷，即线性刚度k为负（屈曲）的情况。对模型（15）引入尺度变换，得到

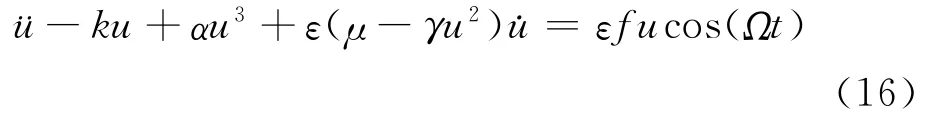
2 混沌阈值的确定

式（19）表示系统的未受扰保守系统可表示为

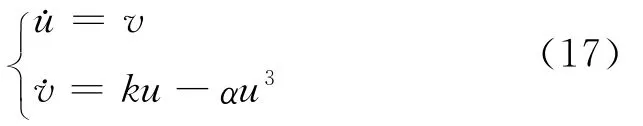
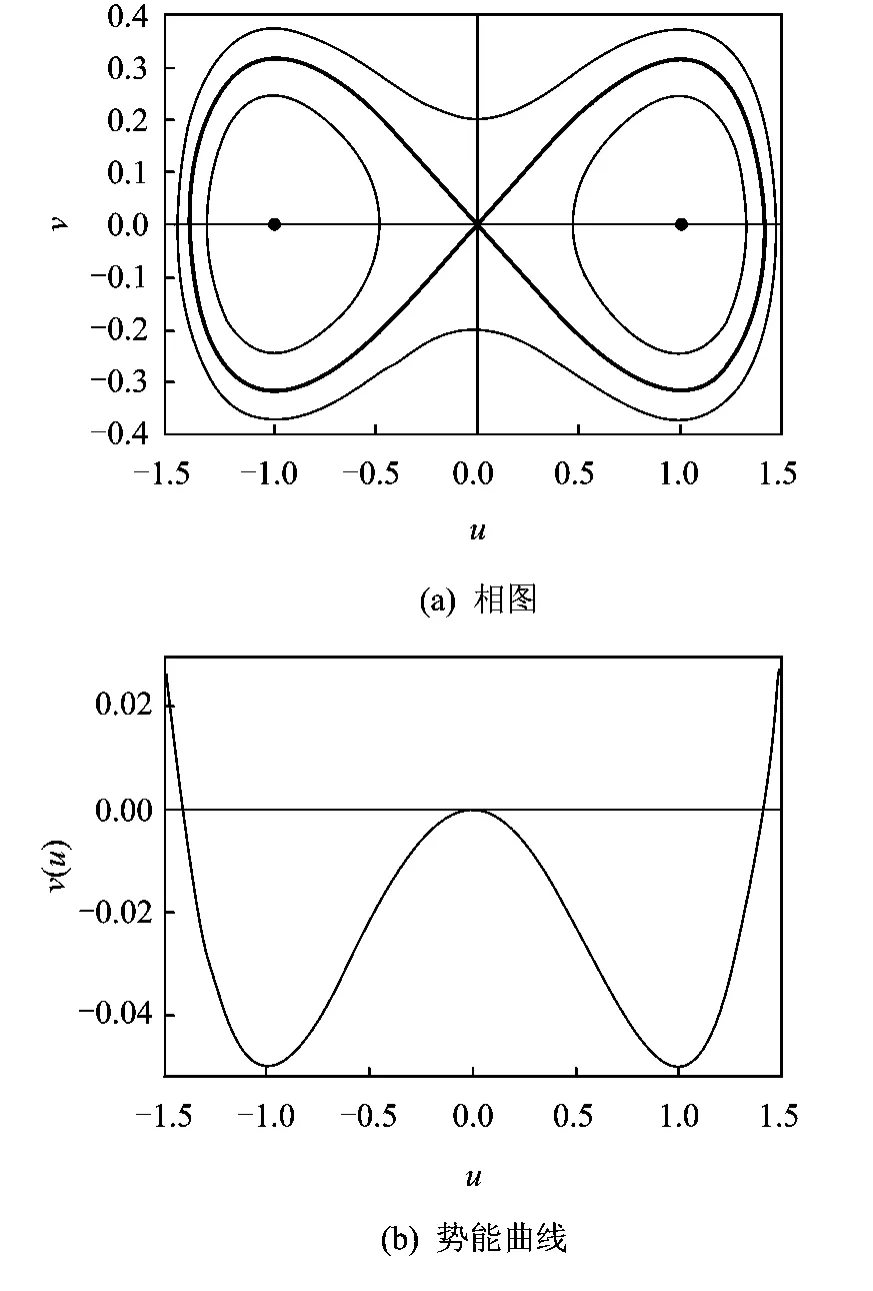
图4 未扰系统的相图和势能曲线

传统的判断系统发生混沌的Melnikov函数可表示为

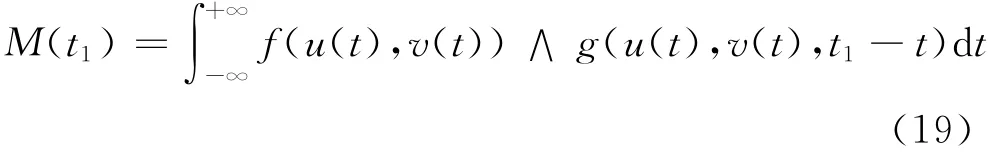
其中

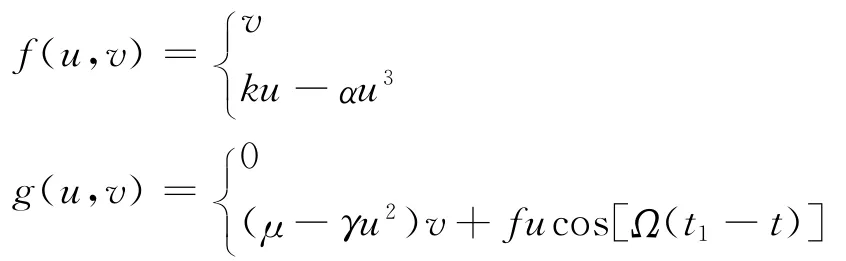
Melnikov函数在M≡0时即为发生Smale马

蹄混沌的阈值。计算得到

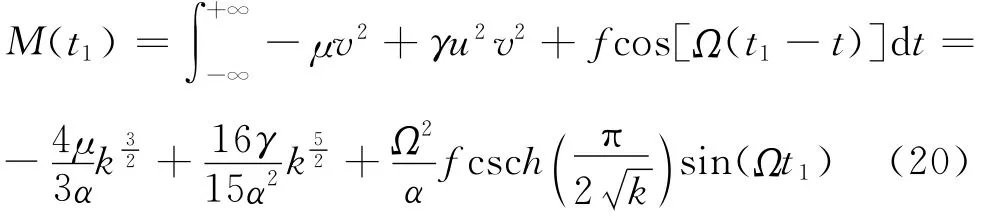
事实上，式（20）得到的阈值只是发生混沌的必要条件而非充分条件，为了得到更精确的混沌阈值可考虑式（16）中各非线性扰动对同宿轨道中刚度k的影响，从而得到改进的Menikov函数。

采用待定固有频率法［9］求得系统受扰动后的待定固有频率ω10，采用复数形式的规范形理论［10］求解该系统。引入复数变量ζ和z

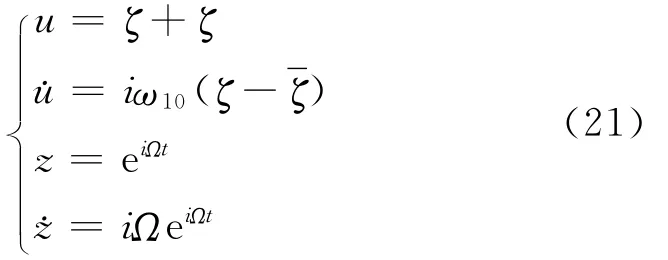
其中：ζ表示ζ的共轭。

求解式（21）可得

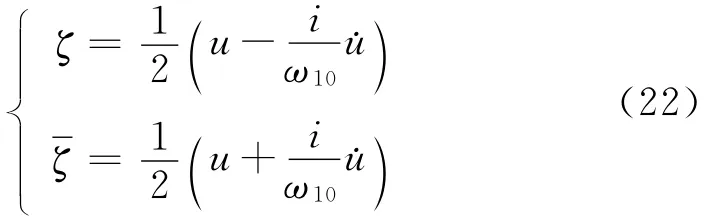
对式（22）中的第1个公式对时间求导，并考虑式（16）和式（21）可得

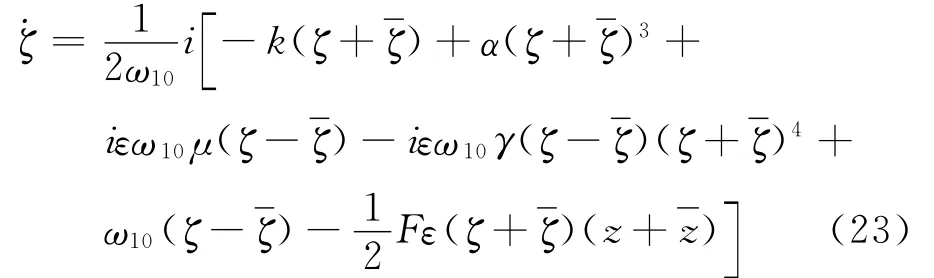
引入直至三阶的非线性变换，化简式（21）得到系统的规范形为

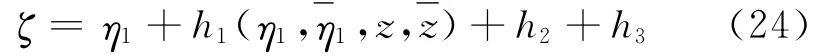
考虑最具有一般性的主参数共振情况Ω＝2ω10，计算式（24）的1～3阶规范形为

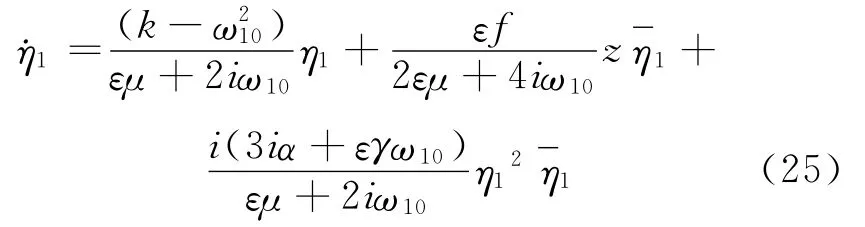
把式（25）中的变量η和z表示为极坐标形式

分离式（25）的实部和虚部得到

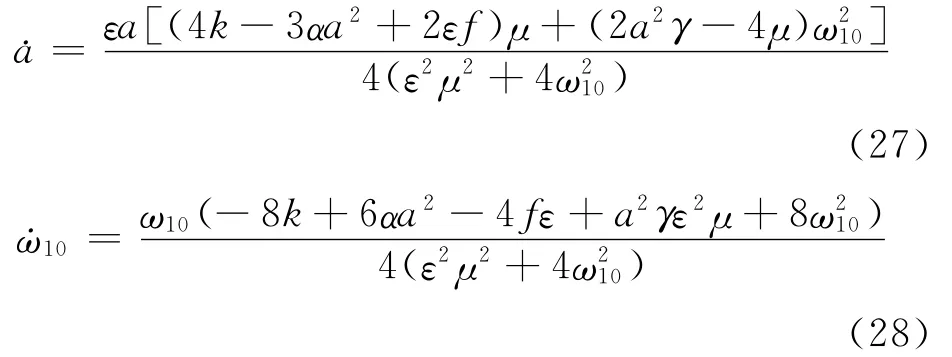
令˙a＝0，得到系统的一阶近似定常解为

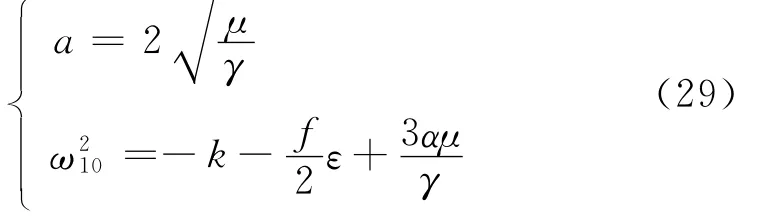
从式（29）的第2式可清楚地观察到，参数激励幅值f、摄动参数ε、非线性刚度系数α及线性阻尼系数μ对系统的振动频率均有影响。

对式（16）引入时间尺度变换T＝ω10t后，在等号两边同除以ω10，可得

式（30）的Hamilton能量函数和势能函数可表示为

当h＝0时，式（31）的同宿轨道可表示为

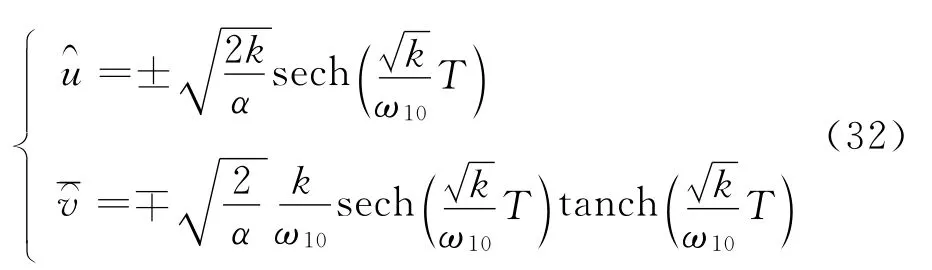
把式（32）代替式（18），带入 Menikov函数式（20），得到改进形式的Melnikov函数

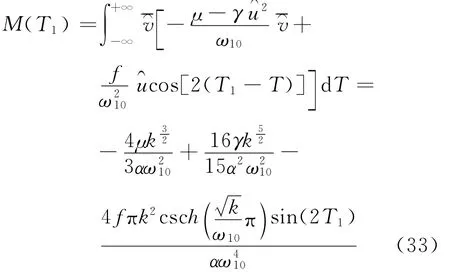
当M（T0）≡0时，系统发生同宿轨道横截相交导致混沌。

3 数值模拟

本研究中取参数值为k＝1，α＝4，γ＝0.22，μ＝0.76，D＝1，Ω＝2，ε＝0.1。系统初值取（0.01，0.01）。根据式（20）及式（33）的判据，计算出传统和改进的两种Melnikov函数阈值，如表1所示。

表1 两种Melnikov方法的阈值比较

图5表示当分岔参数f取接近传统Melnikov方法得出的分岔值时，系统的振幅在一段时间后会趋向一个定值，系统有周期解，因此系统显然没有发生混沌。

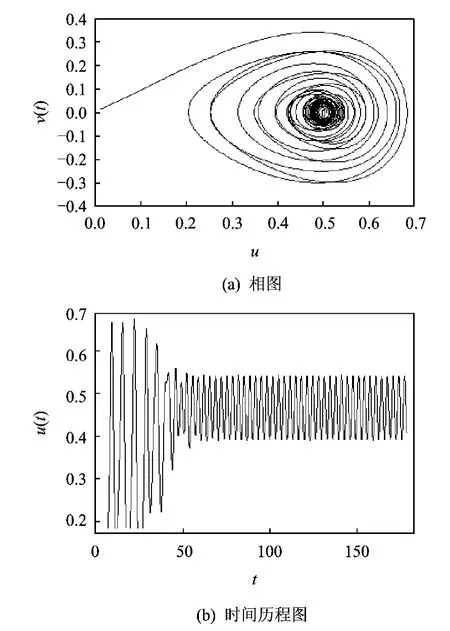
图5 当f＝0.88时系统相图和时间历程图

当取外激励幅值f＝1.89时，系统开始发生混沌，如图6所示。图6（a）发现相轨线在相平面内盘旋绕曲，横截相交。从图6（b）可见，系统的位移围绕两个平衡点振动、跳跃。图6（c）为庞加莱截面图，发现了明显的分形特征，因此可判断系统发生了混沌。

比较图5和图6可知，由于改进的Melnikov函数表达式考虑了系统的非线性系数对系统固有频率的影响，因此计算系统发生混沌的阈值更为精确。但是以上分析只研究了一个初值的响应，而混沌是系统对初值的极端敏感依赖性导致的，所以有必要对相平面内众多初值进行混沌的特征研究。

图6 当f＝1.88时系统相图、时间历程图和庞加莱截面图

系统发生混沌时，稳定流形和不稳定流形将发生横截相交，在相平面内盘旋缠绕成复杂结构，某些初始点出发的相轨线将穿出系统的安全域边界，从而导致系统的不安全，这种现象在很多文献中称为安全盆的侵蚀现象。很多时候系统的安全盆受到侵蚀时，相轨线不断逃逸出安全盆，并再回到安全盆内，因此安全盆边界将呈现分形形状，而安全盆的分形边界是产生混沌的一个重要判据［11－12］。

为了研究系统的激励对安全盆的影响，在相平面内描绘一个包含未扰系统安全盆的区域G

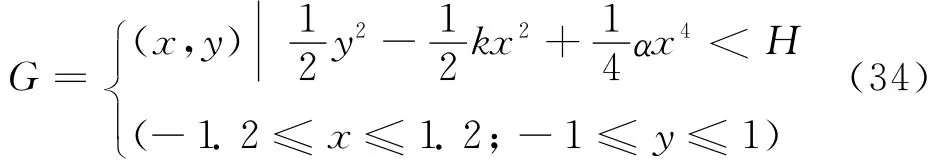
其中：H为系统的总能量上限。

考虑系统总能量不超过H＝0.1，此时系统的运动可能为包含3个平衡点的大范围运动，也可能为两个中心附近的小范围运动，且运动的幅值不至于太大。把区域G划分为步长h＝0.002的小格子，把每个小格子作为系统的初值。当某个初值在时间步长为0.01，迭代计算2×105次后仍然留在安全盆内，可认为该初值是安全的，否则认为该初值是不安全的，在安全盆中删除。

图7（b）显示，激励满足混沌判别式时，系统发生混沌，系统安全盆的边界受到侵蚀。随着激励幅值f1增大，系统安全盆的内部出现分形的情况更明显，如图7（c）所示。安全盆的内核部分（未扰系统的两个中心附近）仍然是绝对安全的，而外围部分区域就不能保证绝对安全。

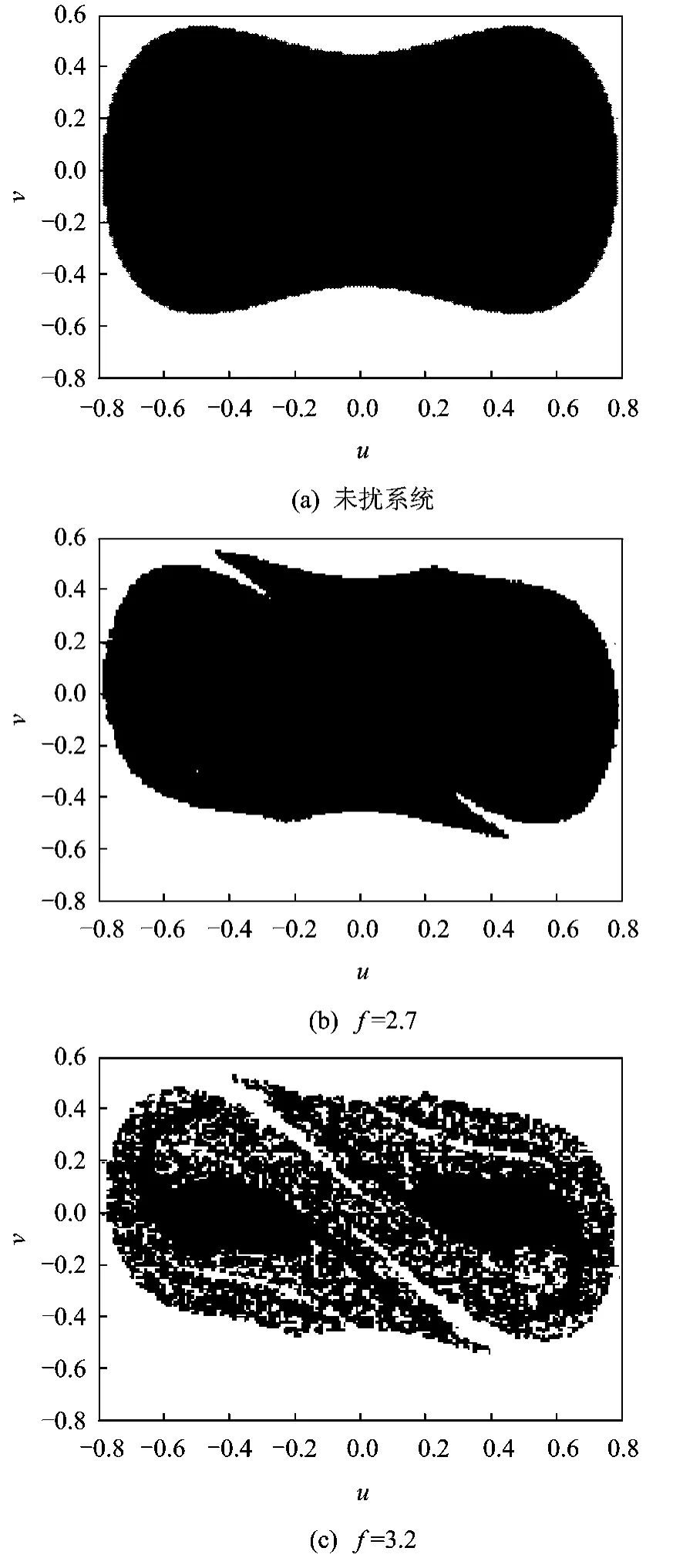
图7 系统的安全盆

4 结束语

通过建立形状记忆合金的连续光滑应力－应变模型，得到了简支形状记忆合金层合梁的动力学模型，化简后振动方程为一个具有负刚度的杜芬－范德坡模型。

待定固有频率法结合规范形理论可以有效地研究受参数激励系统的响应频率因受系统非线性系数的影响而产生和固有频率之间的偏差。对原系统引入时间尺度变化后，考虑非线性参数对系统频率的影响，改进形式的 Melnikov方法比传统形式的Melnikov方法计算得到的系统发生混沌的阈值更精确。

安全盆的边界分形给判断混沌提供了除Melnikov方法之外的依据。安全盆可以清晰地判断初值对系统稳态运动的影响。此研究意义在于：系统在较大激励幅值下即使发生混沌，只要把初值取在安全盆内的安全区，系统的能量也不会超出许可限制。这为系统的健康工作提供了参考依据。

［1］ Collet M，Foltete E，Iexcellent C.Analysis of the behavior of a shape memory alloy beam under dynamical loading［J］.European Journal Mechanics，A－Solids，200l，20：615－630.

［2］ Hashemi S M T，Khadem S E.Modeling and analysis of the vibration behavior of a shape memory alloy beam［J］.International Journal of Mechanical Sciences，2006，48（1）：44－52.

［3］ Savi M A，Pacheeo P M，Braga M B.Chaos in shape memory two－bar truss［J］.International Journal of Non－Linear Mechanics，2002，37（1）：1387－1395.

［4］ 李映辉，张清泉.形状记忆合金梁动力稳定性［J］.西南交通大学学报，2005，40（4）：453－456.Li Yinghui，Zhan Qingquan.Dynamic stability of a shape memory alloy beam［J］.Journal of Southwest Jiaotong University，2005，40（4）：453－456.（in Chinese）

［5］ 张清泉，李映辉，姚进.形状记忆合金梁动力稳定性及混沌运动［J］.四川大学学报：工程科学版，2004，36（5）：30－36.Zhang Qingquan，Li Yinghui，Yao Jin.Dynamic stability and chaotic m otion of a shape memory alloy beam［J］.Journal of Sichuan University：Engineering Science Edition，2004，36（5）：30－36.（in Chinese）

［6］ Wu Zhiqiang，Zhang Zhenhua.Force displacement characteri stics of simply supported beam laminated［J］.Acta Mechanica Sinica，2011，27（6）：1065－1070.

［7］ 葛根，竺致文，许佳.形状记忆合金梁在简谐和白噪声联合激励下的混沌及安全盆侵蚀现象［J］.振动与冲击，2012，31（23）：1－6.Ge Gen，Zhu Zhiwen，Xu Jia.Chaos and fractal boundary of safe basin of a shape memoray aolly beam subjected to hamonic and white nosie excitations［J］.Journal of Vibration and Shock，2012，31（23）：1－6.（in Chinese）

［8］ 王征，陶宝祺.智能材料结构的振动抑制［J］.振动、测试与诊断，1995，15（1）：47－51.Wang Zheng，Tao Baoqi.Vibration suppression of smart material structure［J］.Journal of Vibration，Measurement ＆ Diagnosis，1995，15（1）：47－51.（in Chinese）

［9］ Nayfeh A H.Method of normal forms［M］.New York：John Wiley ＆Sons，2002：14－17.

［10］Wang Wei，Zhang Qichang.The application of the undetermined fundamental frequency for analyzing the critical value of chaos［J］.Acta Physica Sinica，2009，58（8）：5162－5169.

［11］Lin H，Yim S C S.Analysis of a nonlinear system exhibiting chaotic，noisy chaotic，and Random behaviors［J］.Journal of Applied Mechanics Transactions of the Asme，1996，63：509－516.

［12］Gan C B.Noise－induced chaos in a quadratically nonlinear oscillator［J］.Chaos，Solitons ＆ Fractals，2006，30：920－929.