漂浮基柔性关节空间机器人奇异摄动鲁棒控制*

谢立敏，陈 力

（1.福州大学机械工程及自动化学院 福州，350108） （2.福建农林大学机电学院 福州，350002）

引 言

空间机器人不仅可以降低宇航员在宇宙环境中工作时遇到的危险、保证空间活动的安全性，还可以减少成本，提高生产效率和经济效益；因此，空间机器人技术已成为最具有吸引力的研究领域之一，与其相关的动力学控制研究也成为研究的重点和热点［1－3］。值得注意的是，在空间实际应用中，空间机器人并不一定为纯刚性体，它往往具有柔性的特性［4］，主要表现为臂柔性和关节柔性。这些柔性因素的存在使空间机器人在运动过程中不可避免地产生变形和振动，影响系统的控制精度和稳定性。目前，柔性空间机器人的研究大多集中于柔性臂空间机器人［5－7］。柔性关节的存在会使得空间机器人机械臂的运动不再与驱动其运动的电机转子的运动保持完全一致。因此，若在空间机器人的动力学建模和控制方法的设计过程中忽略关节呈柔性的这一特性，空间机器人运动控制的精确性和稳定性将会受到很大影响。由于空间机器人为载体自由漂浮的无根多体系统，载体与机械臂之间存在着强烈的动力学耦合关系；参数、负载和燃料等的变化使得空间机器人的系统参数存在不确定性，这些因素导致惯常用于地面机器人的控制方法难以直接推广和应用到漂浮基柔性关节空间机器人的控制当中；因此，漂浮基柔性关节空间机器人控制方法的设计就变得更加困难。Steve等［8］基于扩展卡尔曼滤波器设计了一种自适应控制方法，以实现柔性关节空间机器人系统运动轨迹的渐近跟踪，但该方法未对系统的弹性振动进行抑制，控制精度不高。潘博等［9］建立了柔性关节空间机械臂的模型，但该模型是建立在载体固定的基础上，不符合空间机器人载体自由漂浮的实际。陈志勇等［10］利用关节柔性补偿器等效降低关节的柔性，研究了漂浮基带柔性铰空间机器人的动力学建模与运动控制。

笔者针对漂浮基柔性关节空间机器人系统，利用系统动量、动量矩守恒关系和拉格朗日第2类方程建立系统动力学方程。基于奇异摄动理论，建立了系统的奇异摄动模型，将系统分解为表示刚性部分的慢变子系统和表示弹性振动部分的快变子系统。设计了以慢变子系统的鲁棒控制方法和快变子系统的线性速度反馈控制方法相结合的混合控制方法。通过计算机MATLAB数值仿真实验证明了所提出方法的有效性。

1 漂浮基柔性关节空间机器人的奇异摄动建模

以图1所示的漂浮基柔性关节空间机器人为例，该系统由载体B0、柔性关节O1，O2、刚性杆B1，B2和固定于B2上简化为质点的载荷P组成。建立系统的惯性坐标系Oxy和各分体的主轴坐标系Ojxjyj（j＝0，1，2）。假设系统在Oxy平面内作平面运动。载体的姿态角为q0，刚性杆Bi（i＝1，2）的转动角度为qi，关节Oi处驱动电机转子的转动角度为θi。柔性关节可等效为存在于电机转子和杆之间刚度系数为K的无惯量扭簧［11］，如图2所示。当关节Oi处的驱动电机转子转过角度θi时，刚性杆Bi受到扭簧的作用会继续转动一小角度Δi，最终到达qi，Δi＝qi－θi即为角度变形误差。可见，若在动力学分析和控制方法设计时忽略关节柔性的存在，必然将不断累积角度变形误差，影响系统的控制精度。考虑到关节的柔性，在对漂浮基柔性关节空间机器人进行动力学分析时要分别分析由载体、杆和载荷构成的空间机器人系统的动力学和驱动电机的动力学。系统的总动能T为空间机器人系统的动能Tq和驱动电机的动能Tθ之和，即T＝Tq＋Tθ。在空间环境中，忽略重力梯度的影响，系统的总势能仅为柔性关节简化扭簧的弹性变形势能，即系统不受外力作用，遵守动量及动量矩守恒关系。不失一般性，设系统初始动量及动量矩均为零，利用拉格朗日方程得到载体位置、姿态均不受控的漂浮基柔性关节空间机器人系统的动力学方程

柔性关节的存在会产生角度变形误差并引起系统的弹性振动。为了克服这些问题，笔者基于奇异摄动法，将系统动力学方程（1），（2）分解成慢变（刚性）和快变（弹性）两个独立的子系统，并对两个子系统分别设计控制方法［12］。慢变子系统的控制方法τs用来补偿角度变形误差和系统的不确定参数，保证系统的控制精度。快变子系统的控制方法τf用来消除系统的弹性振动。于是，系统的混合控制方法为τ＝τs＋τf。

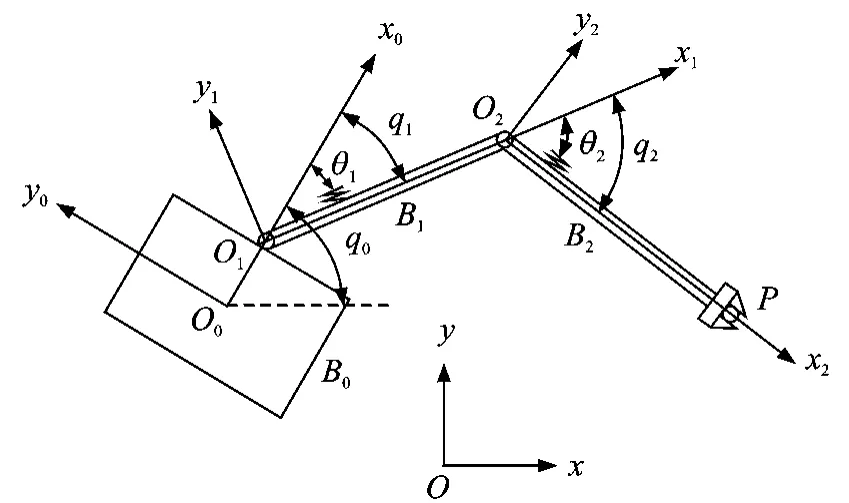
图1 漂浮基柔性关节空间机器人

图2 柔性关节的简化模型

定义正定、对角矩阵K1＝K·ε2，其中，ε为一非常小的正常数。令系统的“快”变量为z＝K（θ－q），则系统动力学方程（1），（2）可重新写为

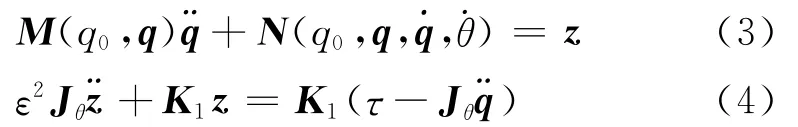
设计快变子系统的线性速度反馈控制方法

其中：Kf＝K2／ε；K2为正定、对角矩阵。

将式（5）代入式（4），获得快变子系统的动力学方程

由于ε为一非常小的正常数，则由K＝K1／ε2可知：当ε→0时K→∞，此时关节等效为刚性。于是，令式（1），（2）中θ＝q，可获得漂浮基柔性关节空间机器人的等效刚性模型，即慢变子系统的动力学方程为

式（6）和式（7）构成了漂浮基柔性关节空间机器人的奇异摄动模型。

2 慢变子系统的鲁棒控制方法

为了便于慢变子系统控制方法的设计，先对式（7）进行准线性化处理，得到

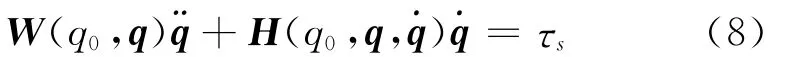
式（8）中的相关矩阵具有以下的性质。

性质1 惯性矩阵 W（q0，q）有界，即 0≤其中：λmin｛＊｝和λmax｛＊｝分别为矩阵＊的特征值的最大和最小值。

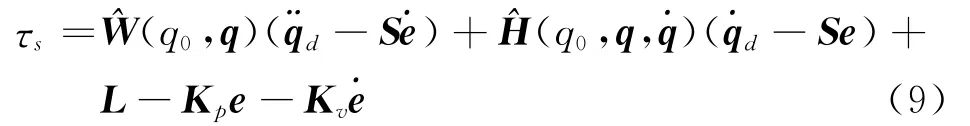
同理，有

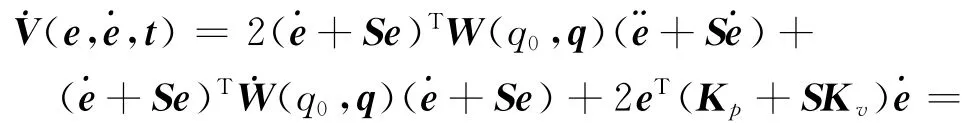
定义μ＝（˙e＋Se）ρ，鲁棒项L可设计为

选取以下形式的Lyapunov函数

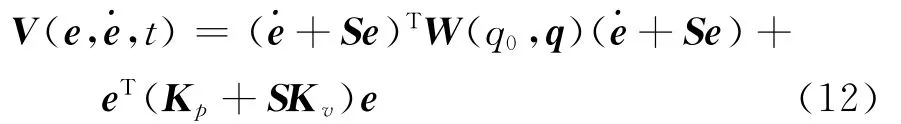
利用性质1和范数的定义，可将式（12）写为

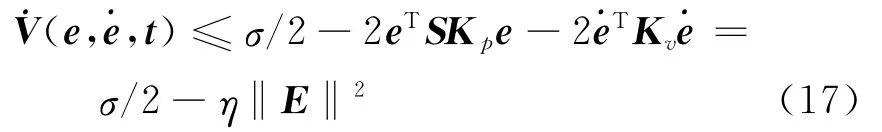
由于σ为一很小的正常数，故易满足σ／2－η‖E‖2≤0，即˙V（e，˙e，t）≤0。根据Lyapunov稳定性定理，系统全局稳定且收敛值为‖E‖≤，进而得到

3 仿真算例

以图1所示作平面运动的漂浮基柔性关节空间机器人系统为例进行MATLAB数值仿真实验。仿真时，假设载荷的质量mp及中心惯量矩Jp为系统的不确定参数，其真实值为mp＝2kg，Jp＝1.25 kg·m2，估计值为mp＝1kg，Jp＝1kg·m2。假设空间机器人刚性杆转角的期望运动规律为qd＝［sin（0.2πt） cos（0.2πt）］T；运动初始值q（0）＝［0.2 1.1 ］T，θ（0）＝［0.2 1.1 ］T，单位为rad；仿真时间t＝10s。图3为漂浮基柔性关节空间机器人刚性杆转角的实际运动轨迹和期望运动轨迹对比图。图4为驱动电机转子的实际运动轨迹与刚性杆转角的期望运动轨迹对比图。图5为关闭快变控制τf后，漂浮基柔性关节空间机器人刚性杆转角的实际运动轨迹和期望运动轨迹对比图。图6为驱动电机转子的实际运动轨迹与刚性杆转角的期望运动轨迹对比图。

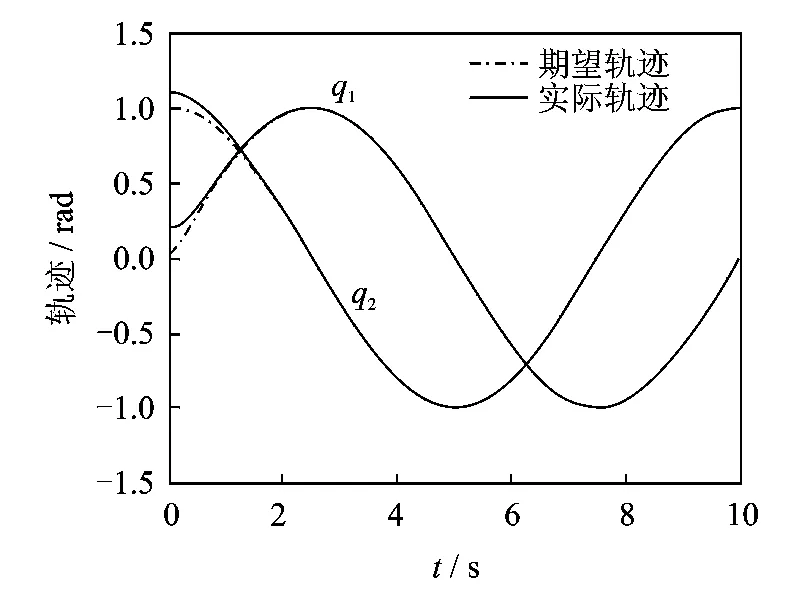
图3 空间机器人刚性杆转角运动轨迹

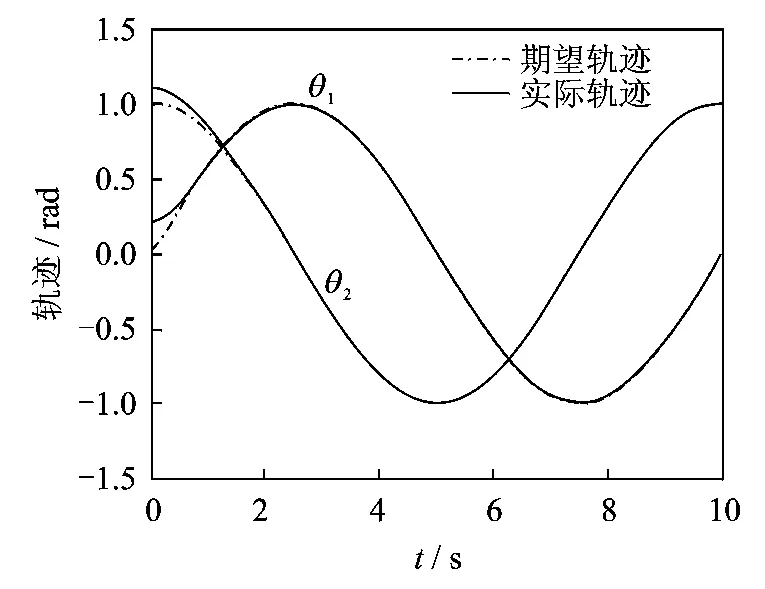
图4 驱动电机转子运动轨迹

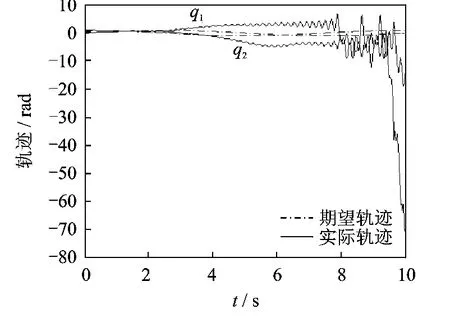
图5 当τf关闭时空间机器人刚性杆转角运动轨迹

由图3和图4可看出，在笔者提出的混合控制方法的控制下，漂浮基柔性关节空间机器人的刚性杆和驱动电机转子都能精确且稳定地跟踪上相同的期望运动轨迹。系统的角度变形误差和参数不确定性均得到补偿，弹性振动得到抑制。从图5和图6可看出，当关闭快变控制τf时，漂浮基柔性关节空间机器人的刚性杆和驱动电机转子的运动都存在剧烈的振动，控制失效，从而证明了快变控制律τf对系统振动抑制的有效性。

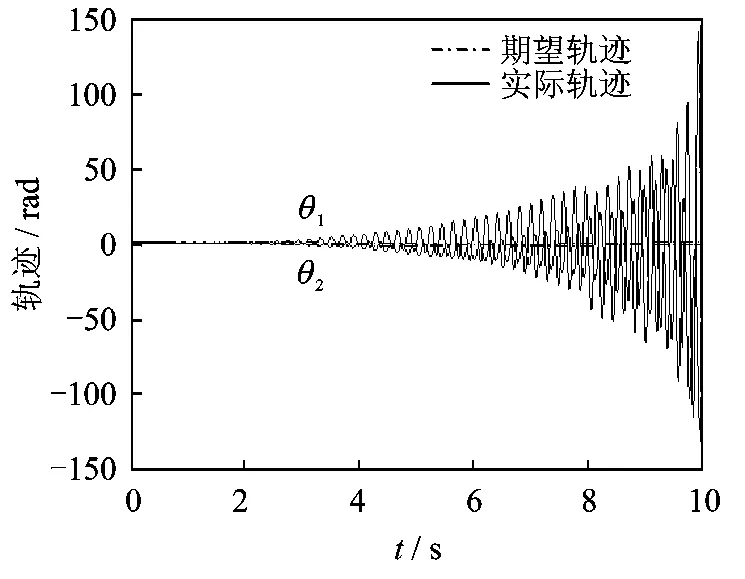
图6 当τf关闭时驱动电机转子运动轨迹

4 结束语

针对漂浮基参数不确定的柔性关节空间机器人，基于奇异摄动法建立系统奇异摄动模型，提出了由慢变子系统的鲁棒控制方法和快变子系统的速度反馈控制方法组成的混合控制方法。数值仿真结果表明，提出的混合控制方法能够有效补偿系统参数的不确定性，消除柔性关节引起的角度变形误差，实现系统运动轨迹的渐进跟踪；同时能够有效抑制柔性关节引起的系统弹性振动，保证控制系统的稳定性。

［1］ Yoshida K.Engineering test satellite vii flight experiments for space robot dynamics and control：theories on laboratory test beds ten years ago，now in orbit［J］.International Journal of Robotics Research，2003，22（5）：321－335.

［2］ 王从庆，柯昌俊.自由浮动柔性空间双臂机器人的混合抑振控制［J］.振动工程学报，2009，22（1）：31－35.Wang Congqing，Ke Changjun.Hybrid vibration suppression for a free－floating flexible dual－arm space robot［J］.Journal of Vibration Engineering，2009，22（1）：31－35.（in Chinese）

［3］ 陈力.参数不确定空间机械臂系统的鲁棒自适应混合控制［J］.控制理论与应用，2004，21（4）：512－516.Chen Li.Robust and adaptive composite control of space manipulator system with uncertain parameters［J］.Control Theory ＆ Applications，2004，21（4）：512－516.（in Chinese）

［4］ 孙玉国，刘海江，孙玲玲，等.刚柔耦合动力系统固有振动特性研究［J］.振动、测试与诊断，2003，23（1）：48－50.Sun Yuguo，Liu Haijiang，Sun Lingling，et al.On natural vibration characteristics of a rigid－flexible dynamic coupled system［J］.Journal of Vibration，Measurement ＆ Diagnosis，2003，23（1）：48－50.（in Chinese）

［5］ 陈志勇，陈力.柔性空间机械臂振动抑制的模糊终端滑模控制［J］.振动、测试与诊断，2010，30（5）：481－486.Chen Zhiyong，Chen Li.Fuzzy terminal sliding mode control of vibration suppression of flexible space manipulator［J］.Journal of Vibration，Measurement ＆Diagnosis，2010，30（5）：481－486.（in Chinese）

［6］ Senda K，Murotsu Y.Methodology for control of a space robot with flexible links［J］.IEEE Proceedings of Control Theory and Applications，2000，147（6）：562－568.

［7］ 吴立成，孙富春，孙增圻，等.柔性空间机器人振动抑制轨迹规划算法［J］.机器人，2003，25（3）：250－254.Wu Licheng，Sun Fuchun，Sun Zengqi，et al.Optimal trajectory planning of flexible space robot for vibration reducing［J］.Robot，2003，25（3）：250－254.（in Chinese）

［8］ Steve U，Jurek Z S.Extended Kalman filtering for flexible joint space robot control［C］∥2011American Control Conference.San Francisco，CA，USA：IEEE，2011：1021－1026.

［9］ 潘博，孙京，于登云.柔性关节空间机械臂建模、控制与仿真［J］.系统仿真学报，2010，22（8）：1826－1831.Pan Bo，Sun Jing，Yu Dengyun.Modeling，control and simulation of space manipulators with flexible joints［J］.Journal of System Simulation，2010，22（8）：1826－1831.（in Chinese）

［10］陈志勇，陈力.漂浮基带柔性铰空间机器人的动力学建模及奇异摄动控制研究［J］.中国机械工程，2011，22（18）：2151－2155.Chen Zhiyong，Chen Li.Study on dynamics modeling and singular perturbation control of free－floating space robot with flexible joints［J］.China Mechanical Engineering，2011，22（18）：2151－2155.（in Chinese）

［11］Spong M W.Modeling and control of elastic joint robots［J］.Journal of Dynamics Systems，Measurement，and Control，1987，109：310－319.

［12］Subudhi B，Morris A S.The singular perturbation approach to trajectory control of a multilink manipulator with flexible links and joints［J］.Proceedings Institution of Mechanical Engineers，2002，215（1）：587－598.