基于单位步进角的铣削仿真算法研究
2013-12-03王学敏孙大乐孙凤龙吴凤和
王学敏,孙大乐,孙凤龙,吴凤和
(1.宝山钢铁股份有限公司,上海 201900;2.燕山大学机械工程学院,河北 秦皇岛 066004)
0 前言
数控仿真技术是虚拟制造的一个重要分支和基础,不但可以验证数控加工程序的可靠性,而且还能够对切削过程进行预测,其终极目标是虚拟构建一个真实的加工环境,用来仿真和评估各个加工过程对产品质量的影响。在数控仿真系统中,加工过程的动态仿真算法是其核心部分,插补算法的选择直接关系着数控系统的精度、速度和加工能力。目前数控系统中最常用的插补方法是逐点比较法和时间分割法[1-4]。逐点比较法算法简单、容易实现,但由于速度指标和精度指标都很难满足现在零件的加工要求,因此在目前的数控系统中已很少使用。时间分割法插补精度高,误差较低,但几何运算复杂,编程计算量大,特别是在进行圆弧插补时,执行速度十分缓慢。因此,设计一种方法用于简化算法的流程,提高仿真的速度显得尤为重要。
本文基于时间分割理论,提出一种以单位步进角为中间变量的数控加工仿真算法。并通过具体仿真实例,表明该方法可以有效简化算法流程,提高仿真速度。
1 基于时间分割法的直线插补算法
时间分割直线插补通过进给速度F和插补周期T对一个插补周期的进给步长数St进行计算,然后再计算插补点的位置[5],进给步长数的计算公式为

设要加工的直线如图1所示,起点为A(xstart,ystart,zstart);终点为B(xend,yend,zend);将线段AB等分为k段并进行插补,下一个动点设为Pi+1;k为网格划分精度;t为插补次数。

图1 直线插补算法原理示意图Fig.1 Linear interpolation algorithm principle diagram
直线插补具体步骤如下:
(1)根据几何关系,各坐标轴对应的位移增量为

(2)进给步长为
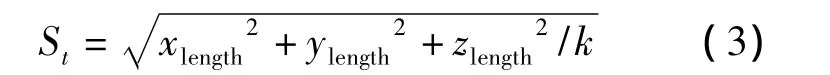
(3)三个坐标方向的步长分别为

(4)每一插补周期的坐标增量为

(5)从而很容易求得下一个动点Pi+1的坐标值为

(6)终点判别:当t>St时,结束。
在对不经过原点的直线进行插补时,需要把原来直线的起点当作坐标原点,建立一个新坐标系。由于该坐标系与原坐标系有关联,因此将插补直线从原坐标系平移到新坐标系即可,无需改动其插补程序。由此可看出时间分割直线插补是一种比较简单的插补算法,此外其进给方向是理论直线,因此不存在理论误差。
2 基于时间分割法的圆弧插补算法
2.1 圆弧插补原理
时间分割圆弧插补是把圆弧视为微小直线段,并用一组直线段来进行逼近,其实质也是直线插补,因此可计算每个插补周期的坐标增量值[6]。
设所要加工的圆弧如图2所示,将插补分为顺、逆两种情况。进给步长计算方法与直线插补相同,圆弧起点为 A(xstart,ystart,),终点为 B(xend,yend),圆弧圆心坐标为M(s,w),半径为R,I为圆弧圆心与起点在X方向坐标的差值,J为圆弧圆心与起点在Y方向坐标的差值,Pi+1(xi+1,yi+1)为下一个动点。弦AP的长度即为每个插补周期进给的步长ΔL,其所对应的圆心角就是每次插补的角步距θ,则有θ=△L/R,并设n为划分精度。
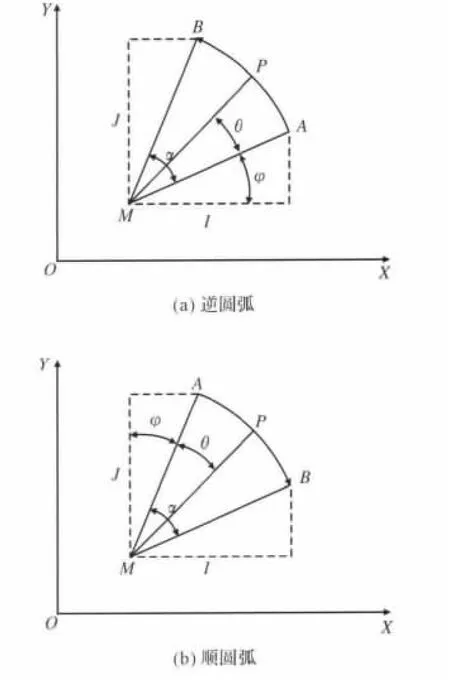
图2 圆弧插补算法原理示意图Fig.2 Circular arc interpolation algorithm principle diagram
圆弧插补具体步骤如下:
(1)A(xstart,ystart)和插补点 Pi+1(xi+1,yi+1)的坐标分别为

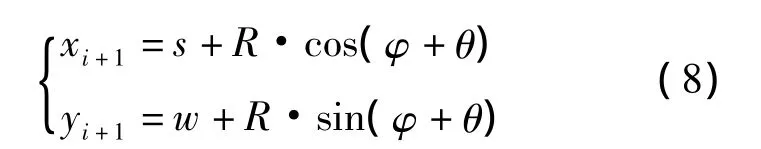
(2)因为θ很小,所以可以做以下近似计算,取二阶近似得
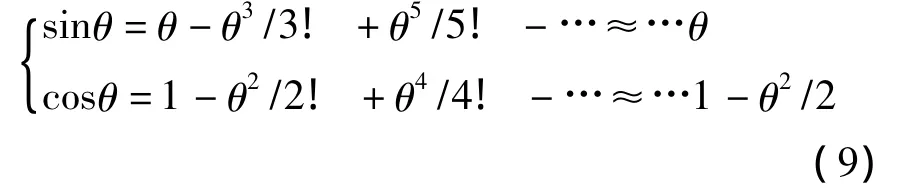
(3)由式(8)、式(9)可得到如下变换,逆圆弧时

(4)顺圆弧时,如图2(b)所示,有
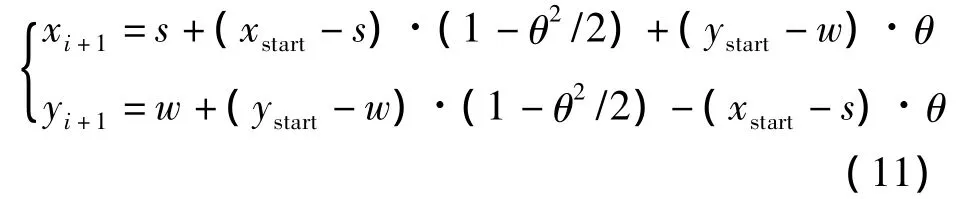
圆弧插补算法对各个象限的插补都适用,解决了插补象限坐标轴的变换和进给方向符号判断问题,大大降低了程序的复杂性,此外,计算简便,避免了三角函数的复杂运算,提高了运算速度,但需要重复迭代来计算插值剩余量,不能满足铣削仿真实时性的要求,影响了加工过程的可靠性和高效性。
2.2 改进的圆弧插补原理
对圆弧插补算法进行改进的主要思想是:在原有的圆弧插补基础上,使用单位步进角作为中间变量,从而在提高运算速度的同时简化运算程序的复杂性,以提高插补速度。
(1)已知圆弧圆心坐标为M(s,w),半径为R,则


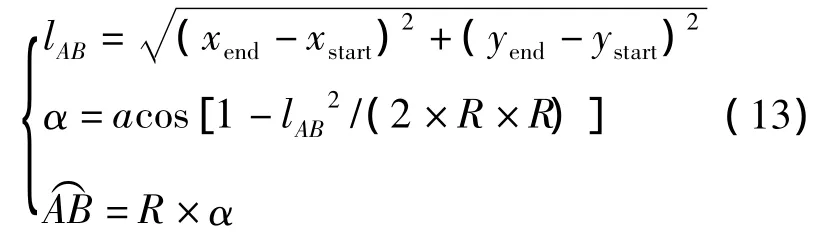
(3)步数 St为

(4)单位弧长l为
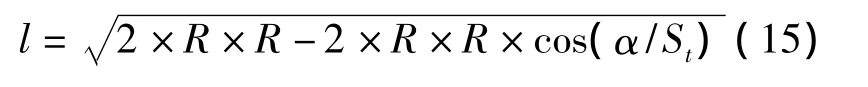
(5)设单位弧度角为θi,则
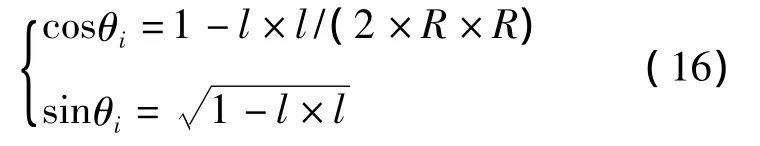
(6)逆圆弧时,如图2a所示,有

(7)顺圆弧时,如图2b所示,有

(8)终点判别为:当t>St时,结束。
与先前圆弧插补算法相比,改进后的插补算法只有每个插补周期各坐标的进给步长的计算公式不同,其余步骤都是一样的。因此,算法改进后,使得插补算法简便,避免了复杂的分象限问题,几何运算简便、函数不需多次调用,可以较为精确快速的进行插补,插补精度可以控制,插补终点判别简单可行,易于编程,适用于任意圆弧的插补,为插补软件的开发提供借鉴指导。
3 铣削算法实时性验证
当在工件上进行铣削加工仿真时,若加工所用的实际时间和理论数控机床加工所用的理论时间一致,则满足加工仿真的实时性需求。在已知进给步数St和插补周期T的情况下,走St步的时间即为T×St。这个时间即为理论数控机床加工时间,将这个时间同实际秒表测量的时间比较,即可得到结果。如下将针对所提出算法以超重型铣镗床为例予以验证。
3.1 直线加工实例
如图3所示,在毛坯上进行一条直线的加工测试,已知被测工件的长、宽、高分别为9 600 mm、4 800 mm、4 200 mm。实验过程中需要让刀具走刀距离设置的大些,以减小测量者的反应误差带来的影响。S为工件上A点到B点距离,A点坐标(800,2 800,4 000)、B点坐标(8 800,2 800,4 000)。实验加工过程如图 4所示。

图3 直线加工Fig.3 Linear processing
图4 直线加工实例Fig.4 Instance for linear processing
已知周期T=0.08 s,代入公式(1)~(6),经过计算可以求得总步长数St=200,这样得到理论上总时间为0.08×200=16 s。经本文直线仿真算法实际加工,得到实测时间如表1所示。
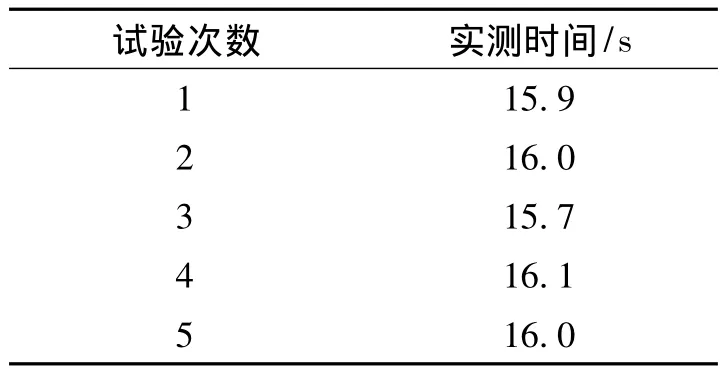
表1 实测时间Tab.1 Measured time
3.2 圆弧加工实例
如图5表示在毛坯上进行一条圆弧的加工测试,已知被测工件尺寸长、宽、高分别为8 000 mm、4 800 mm、4 200 mm。L为圆弧加工路线,已知A点坐标 (-400,7 200,3 800),B点坐标(2 400,4 400,3 800)。实际加工过程如图6所示。

由公式(12)至(18)计算得出,加工该圆弧需要的总步长数St=110,则理论上总时间为0.08×110=8.8 s。经本文圆弧仿真算法实际加工,得到实测时间如表2所示。
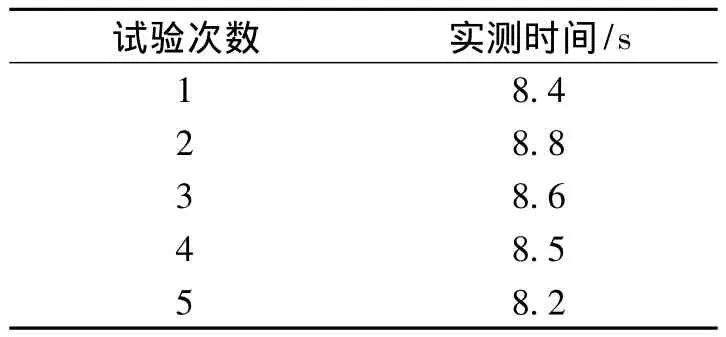
表2 实测时间Tab.2 Measured time
综上实验结果,加工所用的实际时间和理论数控机床加工所用的理论时间基本一致,从而证明了本文仿真算法的可行性和实时性。
4 结论
本文提出的以单位步进角作为中间变量的仿真算法,充分利用了三角函数的符号性,避免了复杂的分象限问题,从而简化了函数调用的复杂性,使得算法简便,提高了仿真速度,仿真实验表明,算法能够保证加工的实时性,具有一定的应用价值。
[1]毕毓杰.机床数控技术[M].北京:机械工业出版社,2006:50-61.
[2]Yong-Kui L.Algorithm for circle approximation and generation[J].Computer - Aided Design,1993,(3):169-173.
[3]孔德彭,张国平,张玉姣.基于圆弧插补的时间分割插补算法改进[J].机械与电子,2010,(2):33-37.
[4]王忠.时间分割圆弧插补新算法[J].组合机床与自动化加工技术,2006,(5):33-34.
[5]仲文祥.基于单片机的经济型数控系统逐点比较插补法的程序设计[J].科技信息,2006,12(3):56-57.
[6]许良元,桂贵生,彭丹丹.高速加工中的加减速控制[J].CAD/CAM与制造业信息化,2005,26(9):66-67.
