从类平均数、变异系数和权重看我国男子十项全能的差距

吴述松，梁东梅，李星儿

South China Normal University，Guangdong 510006，China.

“排位聚类”为竞技体育常态，异时、异地同一竞赛项目的排位聚类现象同样显著。男子十项全能除运动员个体纵向排位聚类外，还有单项评分的横向“水平聚类”。现行成绩－评分转换《田径全能运动评分表》（以简称《评分表》），以十项全能历史比赛成绩［15］为基础，通过复杂数学计算得出，十项目评分简单加总表象，掩盖了内在的事实不等。因此，需要汇总历史数据，以统计分析揭示其不等的加总权数。

“类平均数、变异系数和权重”三维观察、分类视角，为运用一致性的问题导向统计方法对男子十项全能进行拆分和综合立体分析，揭示其三维数据规律提供便利。汇集的运动员比赛成绩可看作同一运动员的多次“训练”成绩，以挖掘十项全能的3个维度，即平均数体现单一项目的能力与水平；方差或变异系数体现技术的稳定性、可控性；受个体能力和2天高强度连续赛制，以及项目之间内在冲突和《评分表》的综合影响，运动员主动、被动强化、“放弃”项目中所蕴含的隐形不等加总权重。运动员对这3个维度不同组合训练及其竞赛策略，决定了其成绩、排位和类别的基础，也是总评分提升的根基。因此，抽象运动员个体差异，会选择性训练和有“田忌赛马”策略的运动员可以取得高总评分及好名次，甚至冠军；不会选择的名次靠后，即使努力使得某单项成绩上升，但不能改变名次，反而抑制潜力。

1 我国男子十项全能“弱势项目提升陷阱”

1.1 《评分表》、赛制和项目之间的内在矛盾与冲突影响男子十项全能

1.1.1 《评分表》对十项全能的决定性作用

国际田径联合会的《评分表》，对十项目采用了边际递增的、区别的甚至偏见［17］的成绩——评分转换规则。使s、m为基本单位的成绩可加总，并比较：A×（B－T）C和A×（D－B）C分别为竞赛、田赛成绩－评分转换公式［15］，其中，T单位为s，D单位为 m，A、B、C为完全不同系数。自1912年第1份《评分表》实施以来，争论不断，但丝毫没有影响它对十项全能运动的决定作用。《评分表》依然是运动员选拔、训练和名次的标杆。巴罗辛认为，新的评分表将引起训练方式的变化，并且要更注意全能各单项的成绩［1］；John认为，改变评分表规则也就改变了运动［15］，杨存斌［11］、Wim［17］持相同观点。事实上，各大赛事十项全能运动员偏少、参与度低，与深刻认识《评分表》有关。

1.1.2 赛制影响

比赛首项评分平均数高，而1 500m最末项，评分最低；第1天的跳高和第2天的撑杆跳高获得基准成绩后，分别为3cm和10cm的升杆规定，其标准方差均为中位数。

1.1.3 项目之间的内在矛盾与冲突

第一，技术规范不同。与初速度正相关的动能和抛物线运动2个原理直接影响田赛项目，但非直接影响径赛项目。

第二，身体要求不同。铁饼、铅球要求高大身材，跳高、撑杆跳、1 500m等要求精干体形。

第三，生理要求不同。1 500m耐力主要来源为糖酵解的混氧代谢，而其余9项的爆发力与速度的能量取决于磷酸源、糖酵解代谢。

第四，受体能约束而差别对待连续2天竞技。运动员不可能均衡对待10单项，没有运动员在10个项目上都出色［16］。

1.2 寻找关键因子和关键项目研究的误区

有数据分析研究企图发现、找到十项全能的关键因子和项目，尤其是弱势项目，主要有因子分析法［3］——从10个单项评分数据中提取共性因子［7］。但面临四大难题：

第一，违背全能和全面［7］原则——不要让单一项目突出的运动员的总评分超过其他几个项目优秀的远动员的总评分。

第二，评分“中间变量”对评分而非成绩数据的因子分析意义打折扣，《评分表》复杂的成绩－评分变换，信息转轨大，研究结论大相径庭，甚至误导训练、比赛，例如，Cox等［13］认为，《评分表》偏向田赛项目，而John［15］的经验研究结论认为偏向110m、110m栏和400m竞赛项目。

第三，特征值累积速度慢，因子选择难。本研究与因子分析法对应的主成分方法也证明了这一点，可获得的共性因子无非是径赛、田赛，或者是身体条件、技术和耐力等自然扩展。

第四，《评分表》已经区分了径赛和田赛“因子”，即从跑、跳、投3个因子，或者力量、爆发力、技术（含运动心理）和耐力［17］4个因子来比较。由于因子分析局限性，西方学者常添加变量并拓展方法，如Valentin Wimmer［16］就运用潜变量模型（LVMs）去综合因子分析的不足。

1.3 我国十项全能差距被拉大

2005年，齐海峰的8 290分为男子全国纪录，而近年来，我国十项全能成绩不理想，各级赛事都未突破8 000分，且与冠军差距日益扩大。2008年北京奥运会，齐海峰以7 835分列18位，2009年第11届全运会上夺冠，仅得分7 941分；余滨在2010年广州亚运会的7 586分，倒数第二。8 290分可进入北京奥运会和2011年世界田径锦标赛前5名、伦敦奥运会第7名，但与2008年北京冠军差501分，与2009年柏林世界田径锦标赛冠军差500分，与2012年伦敦奥运会冠军差579分，与世界纪录差736分。

1.4 关键项目研究令我国男子十项全能进入“弱势项目提升陷阱”

李铁录［5］和徐茂典［10］的研究泛化“木桶原理”，认为要通过短板——突破1 500m来提升十项全能水平。广州亚运会上，韩国运动员金建佑凭借1 500m的第1名，总分从倒数第一跃至亚军；另外，十项全能冠军“都怕”1 500 m，比如广州亚运会冠军卡尔波夫的1 500m，倒数第一。事实上，提升1 500m成绩，似乎是我国男子十项全能实践和理论工作焦点，齐海峰由中长跑改十项全能，他的1 500m与世界冠军差距最小，甚至超过一些赛事的冠军。

理论上，从1995年的曹效文［2］开始，王文清（1997）、李新 华 （2001）、王 强 （2003）、贾 明 学 （2003）、金 红 珍（2006）等研究者都认为，1 500m为我国男子十项全能的突破口，梁建认为，1 500m与其他几项比较，还有很大的提升空间［3］。我国男子十项全能却因为相对提升1 500m成绩而陷入总评分不升反降陷阱，这与错误选择突破口有关，并导致整个训练系统的错位［8］。本研究与John结论一致，整体看，1 500m为现阶段十项全能整体的弱项而被“放弃”——无十项全能职业运动员在1 500m上花费功夫［15］。122人次的1 500m评分总和，只占8.3%的总评分和，小于10%。

1.5 我国十项全能差距的关键：未能建立以体能为基础的、有速度性质项目的相对优势

北京奥运会前3名的100m、110m栏和400m的成绩突出。相应地，第11届全运会前3名在100m、110m栏、400m和跳远项目成绩突出。伦敦奥运会、六大赛会122人次的100m、110m栏、400m和跳远4项评分都占十项全能总评分的43.4%，而六大赛会冠军该4项评分和占总评分和的44.1%。

体能是技术和心理双稳定的基础。运动员连续两天竭力竞赛，评分平均数的下降趋势和每天的V型图，揭示了体能及其恢复的轨迹（图1）。双V型图1是按比赛顺序（横轴）排列的单项评分平均数，每天第1项成绩偏高，当天的中间项目，即第1天的铅球和第2天的铁饼，因体能大消耗而评分低，说明它们是体能转折关键点（表2和后文伊顿的数据）。受体能约束，第11届全运会与北京奥运会的前8名在双V型和评分下降趋势大致相同。不同在于：1）第11届全运会运动员的体能及恢复差，导致每天的体能转折项成绩快速下滑；2）受提升1 500m成绩的影响——弱项提升后遗症，中国运动员有意识把体能留在第2天，标准方差相对都小，意味着第2天的技术更稳定。这与北京奥运会完全相反，北京奥运会运动员体能运用集中在第1天。

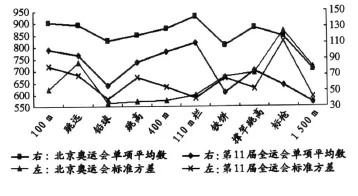
图1 本研究按赛序排列的单项平均数下降轨迹与双V型蕴含的体能消耗与恢复示意图Figure 1 According to the Sequence Arrangement Single Average Falling Trajectory and Double V Containing Its Physical Consumption and Recovery

北京奥运会前8名以速度性质项目为基础（图2），这个结论为后文不等q检验所证明，而第11届全运会前8名的单项平均数排序不同于北京奥运会。这表明，我国男子十项全能采用了与世界顶级运动员不同的训练方式和比赛策略。北京奥运会前8名单项平均数顺序差呈规律性强化与放弃，9个顺序差数的平均数为24.6，而标准方差为29.9；第11届全运会对应数据为27.3和17.4，表明了2者不同的抓放训练方式与竞赛策略。

图2 本研究速度性质项目在十项全能中的起点意义示意图Figure 2 Speed Nature Projects Starting Point in Decathlon

2 一致性问题导向统计方法与数据来源

2.1 一致性问题导向统计方法

《评分表》自有逻辑，十单项也有内在逻辑，鲜有结合二者关系，从可观察的问题出发，寻找逻辑一致性统计方法，全面地而非关键环节地对十项全能的评分数据进行研究。问题导向统计方法是一个有益尝试，且可互证Dawkins等［14］的分类研究结论。从可观察的、单项平均数和标准方差不等实际问题的出发，通过逻辑衔接的问题导向统计方法，寻找不同类别运动员的差异、项目内在冲突，并揭示运动员以主动、被动选择性和重组项目，提升总评分的模式与路径，分为3步。

第1步，评分平均数、标准方差不等——单因素方差分析和q检验法，意味着运动员主动、被动选择性“抓放”项目；第2步，评分权重不同，借助主成分法消除多种共线的线性回归——10项权数不等线性加总，既揭示了掩盖在总评分简单加总表象，又强调了受运动员历史成绩影响，《评分表》对项目的差异对待及其相互强化，并进一步论证对10个项目的全面组合与总评分之间的关系；第3步，冠军类、潜力分化类和双锁定类——聚类分析法，分离出不同类的评分平均数、变异系数和权重的组合模式。以三维度对10个项目的不同选择性抓放及其训练、比赛策略，蕴含着不同总评分与潜力发挥模式。

2.2 全面选择性组合与李氏“补偿”

一致性问题导向统计方法对六大赛会十项全能的122×10个数据统计分析显示，冠军类运动员非常重视以《评分表》的不等参数为指针，化为以平均数所体现的单项水平和以变异系数所体现的技术可控性训练与比赛。因此，在这3个维度组合下，甄选和训练远动员，是取得好成绩的关键。该结论不同于李庆峰［4］的观点，他认为，十项全能有平衡与非平衡2种成绩“补偿方式”，即“避短”和“扬长”。全面选择性组合项目，既有主动发挥优势项目获得领先位置，也有被动适应《评分表》的无奈，而补偿为完全的主动过程，并且可以不受约束。

2.3 数据来源

2008年北京奥运会24人；2009年柏林田径锦标赛34人；2009年山东第11届全运会8人；2010年广州亚运会6人；2011年大邱田径锦标赛24人；2012年伦敦奥运会26人，共122人次的数据来源于官网。

3 一致性问题导向统计方法三过程

受《评分表》、赛制和内在矛盾与冲突影响，十项全能出现了不等的、可观察的单项评分平均数、标准方差（表1）。

表1 本研究122人次10个单项评分平均数、标准方差、总分线性回归的系数和C系数一览表Table 1 122－person＇s individual event scoring averages，standard variances，the total score linear regression coefficients and C coefficient

3.1 检验平均数是否相等

1）单因素方差检验单项平均数是否相等。依据《评分表》“同一尺度、一律平等；符合公正、公平原则”，假定运动员对十项全能无区别对待，10个项目看作同质运动，10×122数据结构仅仅是“分组”结果，组数k＝10，每组有m＝122次“实验”。运用单变量方差分析，检验上述10组平均数在统计上是否相等，即运动员是否同等对待10个项目（表2）。结果显示，F＝65.01，远大于0.05显著性水平下F关键值1.89。因此，有95%置信度认定10个单项至少有2单项平均数不等，即运动员对10个单项有选择性“抓放”区别对待。

表2 本研究122人次10“分组”单因素方差分析一览表Table 2 Single Factor Analysis of Variance for 122－person and 10－group

结果显示，1）1 500m平均数与其他9项目有显著差异，且最低；2）铁饼、标枪平均数无显著差异，但与1到7项目有显著差异；3）铁饼平均数与1到7项目差异显著；4）撑杆跳高与400m平均数无显著差异，但是与1到5项目差异显著；5）跳远、110m栏、铅球和跳高的平均数与撑杆跳高无显著差异，但与100m差异显著；6）100m、跳远、110m栏、铅球和跳高的平均数无显著差异。

因内在的速度、力量和技术的矛盾与冲突，运动员有意、无意及主动、被动“抓放”项目，并通过不同组合提高各自的总评分与排位（表3）。例如，均主攻具有速度性质的项目，100m为代表，平均数高且方差小。2012年奥运会冠军伊顿，铁饼716分排21位，为弱项。1 500m的“成绩普遍偏低”［6］。

表3 本研究α＝0.05显著性水平下，∣X1－Xs∣与关键值34.56比较一览表Table 3 under the 0.05significance level，the absolute value vs.the critical value 34.56

100m与1 500m不相关，与表3逻辑一致，即多练100m及少练1 500m而致不同平均数，且技术不能相互迁移（表4）。表4比表3突出了项目之间的内在冲突，如力量型的铅球与速度型的400m、110m呈现较强负相关。因此，对十项全能的理论和训练要求一个项目技术、训练不能代替另一个项目，项目之间存在高度独立性，比如1 500m和铁饼。当然，一些技术和训练可相互迁移，即有共性技术，比如100m、400m和跳远。这间接证明因项目内在联系与冲突，找共性因子难。

同样方法可检验并排序不等的标准方差。平均数、标准方差不等实证了10个项目之间的内在冲突与矛盾，也蕴含着优秀运动员从自身实际出发，主动、被动地选择项目的客观性、合理性。

表4 本研究122人次10项目之间相关系数及其蕴含的技术可迁移与冲突一览表Table 4 ten projects correlation coefficients and its technology transferring and conflicting for the 122－person＇s scorings

122×10个元素两两项目之间的相关性检验：n－2＝122－2＝120，查5%“相关系数表”，显著性水平相关系数检验值为0.17，即2项目相关系数绝对值≥0.17，则相关，否则不相关。表中相关系数≤0.17的右上角标＊，代表项目之间的技术不可迁移，大负系数表明项目之间的矛盾与冲突。

3.2 多元回归系数权重及其选择性抓放组合

首先，运用主成分法消除多重共线，并以主成分向量做线性回归的解释变量；其次，把主成分向量替换成原始向量，以权重解释运动员对项目的“抓放”。结论表明，1）权重不是决定运动员选择项目的主要因素，即不因成绩的边际评分高而强化该项目，成绩的边际评分低而放弃该项目；2）表5特征值累积占比增长很慢，辅证因子分析法有缺陷。

单项评分列向量标准化，即对（Xij）122×10的列向量标准化成（xij）122×10，并把矩阵xij分块为10个列向量xj，i，j＝1，2，3，…，10。以x1＝100m，x2＝跳远，…，x10＝1 500m（表5、表6）。把表6转化成（Cij）10×10方阵，并分块为10个列向量Cj。

表5 本研究10个特征值及其累积百分比一览表Table 5 10－eigenvalue and its cumulative percentage

表6 10特征值对应10特征向量Table 6 10－eigenvalueandits10characteristicvectors

F1＝－0.35x1－0.4x2＋0.01x3－0.2x4－0.41x5－0.36x6－0.31x7－0.36x8－0.31x9－0.23x10

标准化总评分y（y～N（0，1））为被解释变量，并对主成分向 量 组 Fj做 回 归。 以 （xij）122×10乘 以 （Cij）10×10得 到（Mij）122×10，M 为（xij）122×10经 主 成 分 法 转 换 后 矩 阵，M 与（xij）122×10有相同总方差，且多重线共线消除。（Mij）122×10可分块为10个列向量（Mj）122×1，y对10个项目列向量（Mj）122×1，即Fj对做无多重共线回归（表7）。

表7 本研究＾y对10个主成分Fj的回归参数、t值与概率一览表Table 7 Regression Parameters of Ten Principal Component Fjby＾y，t value and its probability

除常数项外，F1到F10的系数都通过了t检验，且与0差异显著。对截距项、F1到F10系数为0的联合F检验，概率值远小于0.01，故系数不同时为0。截距项虽然很小，但无法通过与0无差异的显著性检验，即截距项正是0。含义是，十项全能总评分完全由运动员的单项评分决定，无其他任何外在因素影响。这就是常说的竞技体育，尤其是高级别竞技“0失误”已经成为最低而非最高要求。靠临场发挥等偶然因素取得好成绩，甚至夺冠的概率越来越小。

把Fj还原成xj的达式，即以F式代入估计方程＾y，转换成＾y是xj的表达式。10个xj系数是（Cij）10×10行向量分别乘以，列向量β＝ （－0.58，0.16，－0.11，0.05，－0.04，0.03，0.01，－0.12，－0.07，－0.06）T而得到。如x1系数，就是表8对应的数据先相乘，后连加。

表8 本研究解释变量x1系数求法一览表Table 8 a way to get the coefficient of the explanatory variable x1

类似方法可求x2到x10系数。因此，还原成xj后，总评分的估计方程为

另外，还可用矩阵法求xj的系数。（Cij）10×10×（β，β，…，β）10×10＝N10×10，矩阵 N 对角线上的元素，依次为xj的系数。

表9 本研究总评分权重分配一览表Table 9 Total Score Weight Distribution

图3 本研究单项评分平均数及其在总评分中的回归贡献（权重）示意图Figure 3 Individual Scoring Average and the Total Score of the Regression Contribution（Weight）

3.3 聚类分析与权重、平均数和变系数组合

表10 本研究122人次的10项评分聚类成一览表Table 10 divided the 122persons into five categories by their ten scoring

图3、图4显示，1）按平均数而非权重抓放项目，冠军类除了1 500m外，其他9项的平均数高；2）潜力、分化类采取了总体一样的策略，可以看做是无选择组合，忽视自身能力、项目内在差别。因此，会出现分层，若有好的理论、尤其是数据分析为指导，成绩可获提升，否则止步不前，甚至滑向双锁定类；3）双锁定类的最大特点是挑战现阶段男子十项全能内在规律，对平均数最低的弱项1 500 m选作突破口，双锁定类以全运会人数为主（表10），而我国十项全能的差距在扩大［9］，违背十项全能阶段规律的权重和平均数，企图逆向突破而入“弱势项目提升陷阱”。

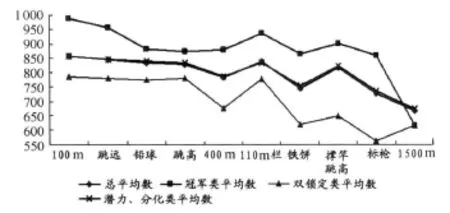
图4 本研究不同类别的平均数比较示意图Figure 4 comparing types of the different averages

变异系数，即单位平均数的标准方差，在运动学中，体现运动员技术的可控性与稳定性，潜在因素有体能。受10个单项之间的内在矛盾与冲突，冠军运动员也难以在连续2天的竞赛中与单项运动员一样。这需要运动员在变异系数所体现的技术可控性与平均评分所展示的水平之间取得平衡。因此，冠军运动员的变异系数随着比赛顺序、体能和项目的技术迁移，在10个项目之间呈规律性的大幅度变化；相反，双锁定类的平均数和变异系数双低，呈现出双锁状态，且无规律变化。双锁定类的1 500m变异系数大幅减少，表明企图在这里实现“关键突破”，并非恰当地提升了技术与体能保证，说明我国十项全能在项目选择、训练和比赛策略上有问题，并导致了其他单项成绩差，变异系数小，形成上升潜力小的另一种双锁定（图5）。

平均数、变异系数的时间规律。连续2天高强度比赛，运动员体能透支与恢复是一个大问题，但通过聚类可以看出，冠军类有按时间自然进展分配体力的趋势，对每一天的先后项目区别对待，且单项评分平均数与变异系数保持大致节奏，原因是力量是技术的基础和保证，没有体能则技术失真。对照其他组别，虽有类似规律但不显著，双锁定类在1 500m上不合时宜的平均数和变异系数的“突变”最为典型。

图5 本研究不同类别的变异系数比较示意图Fgiure 5 Comparing Types of the Different Variation Coefficients

4 结论

男子十项全能10个单项有不同技术规范，也有对运动员体能及恢复的基础要求。虽有《评分表》的“样样精通、面面俱到”的原则约束，但是，优秀运动员及其教练员、科研团队，还是对项目进行主动、被动选择性“抓放”组合。从总评分中对单项的权重、平均数体现的单项水平和以变异系数表示的技术可控性、稳定性3个维度，采用实用的相对优势，而非严格在10个项目上都绝不“输一秒一寸”的平衡、全面优势。因此，恰恰是那些“偏科”的、且“会偏科”的运动员获得冠军，总评分第一和单项倒数第一并行不悖。

指导我国男子十项全能训练、比赛的原则，1）十项全能当今所处的发展阶段离全能、均衡还有差距，违背阶段趋势与规律追求整体的弱项，尤其是大力发展1 500m将制约十项全能整体的发展；2）体能及恢复为男子十项全能的基础，采取策略竞赛，把铅球和铁饼作为体能恢复的转折项目，以体能保证大评分平均数及小标准方差体现的技术可控性，以取得相对优势；3）每天首项的100m和110 m栏，及其技术可迁移的跳远和400m成绩奠定了十项全能的起点。

［1］巴罗辛，乌沙果夫.新的全能评分表［J］.山东体育科技，1985，7（2）：77－80.

［2］曹效文.论1500米在十项全能中的重要性［J］.成都体育学院学报，1995，21（2）：41－44.

［3］梁建，张波.从因子结构比较分析2006年中外优秀十项全能选手的比赛成绩［J］.首都体育学院学报，2008，20（2）：123－125.

［4］李庆峰.对田径十项全能运动员竞技能力非衡结构补偿问题的初步研究［D］.山东师范大学硕士学位论文，2007.

［5］李铁录.我国男子十项全能运动员突破8000分成绩模式及单项成绩水平评价模式的研究［J］.西安体育学院学报，2001，18（4）：53－57.

［6］男子十项全能美国包揽金银牌 伊顿力压哈迪［EB／OL］.http：／／www.sinovision.net／portal.php mod＝view＆aid＝225011.

［7］魏春玲.我国十项全能运动成绩的因子分析及灰色系统回归预测研究［J］.体育科学，2004，24（11）：51－53.

［8］王国祥，刘生杰.中、外优秀男子十项全能运动员的成绩比较研究［J］.中国体育科技，2011，47（6）：14－18.

［9］邬燕红.我国“全运会”与“奥运会”男子十项全能“优势分析”探讨［J］.北京体育大学学报，2007，30（5）：28－31.

［10］徐茂典.第29届奥运会田径男子十项全能前八名成绩分析［J］.体育科学研究，2010，（1）：93－96.

［11］杨存斌，朱谷林.从全能运动评分表的回归分析谈我国女子全能运动的发展方向［J］.北京师范大学学报.1990，35（1）：69－73.

［12］邹克宁，吴洪波.从世界男子十项全能运动发展趋势看我国男子全能运动突破方向［J］.山东体育学院学报，2009，25（8）：78－80.

［13］COX T F，R T DUN.An analysis of decathlon data［J］.J Royal Stati Soc.Series D （The Statistician），2002，（51）：179－187.

［14］DAWKINS B P，P M ANDREAE，P M O＇CONNOR.Analysis of Olympic heptathlon data［J］.J Am Stati Asso，1994，（8）：1100－1106.

［15］JOHN BARROW.Decathlon：the Art of Scoring Points［EB／OL］.www.iaaf.org.http：／／sport.maths.org／content／decathlon－art－scoring－points.

［16］VALETIN WIMMER，et al.Exploring competition performance in decathlon using semi－parametric latent variable models［J］.J Q Analysis Sports，2011，（4）：1－19

［17］WIM WESTERA.Decathlon：Towards a balanced and sustainable performance assessment method［J］.New Studi Athle，IAAF，2006，（1）：39－51.