基于聚类优化的模糊OLAP查询技术研究

(丽水学院工学院，浙江丽水，323000)

0 引 言

联机分析处理(On Line Analytical Processing，OLAP)是一种多维的分析查询方法，它能在数据仓库的基础上，提供“What if”的分析功能[1、2]。然而实际的分析过程中，用户可能关心的是某一个范围内的聚集值，并不仅仅是某些具体维度的聚集值，对于超市海量数据的分析人员来说，对于不同年龄段的顾客购物情况进行分析，可能比根据每个年龄生成对应的顾客购物情况的报表更有意义;同样，对于银行贷款数据分析人员来说，按企业规模与利润规模来进行分析更有意义[3，4]。这些查询带有一定的模糊性，无法直接在数据库或多维数据集上实现，通过引入模糊查询来解决这一问题，引起了研究者的广泛关注。但是，在目前的研究中，对于模糊OLAP查询的常用处理方法是先进行聚类，然后根据隶属度函数进行计算[5]，但由于在计算的过程中对于许多隶属度低的单元格也进行了聚类计算，导致效率不高，特别是在多个维与层次上都有模糊性的查询要求时，其影响更加明显。基于以上分析，本文提出了基于过滤机制的模糊OLAP查询优化算法，其基本思路是在进行聚类计算时，对数据元组进行模糊隶属度函数动态计算，尽早的发现并淘汰隶属度过低的元组，从而提高查询的整体效率。

1 模糊OLAP查询及操作的形式化描述

本文对OLAP的模糊查询中使用的相关概念及其计算公式进行详细的形式化描述。

定义1(模糊值)模糊值fuzzy_v可用一个三元组＜VName，μ，λ ＞表示。其中VName为模糊值的概念，μ为隶属度函数，λ为隶属度阈值。

定义2(维模糊值)对于OLAP 多维数据集上的维D，假设其有k个层次，则这个维上的维模糊值fuzzy_D形式化描述如下:(v0，v1，…，vk)，其中vi(0≤i≤k)或者为一个确定的数值，或者为一个模糊值。

定义3(模糊OLAP查询)对于某个OLAP 多维数据集，假设其有d个维，则这个OLAP 多维数据集上的模糊OLAP查询fuzzy_v可以形式化描述为[fuzzy_D0，fuzzy_D1，…fuzzy_Dd]，其中fuzzy_Di(0≤i≤d)为维Di上的维模糊值。

由定义可知，模糊OLAP查询是对传统OLAP查询定义的扩展，从而可以用统一的观点来处理传统的OLAP查询与模糊OLAP查询。同时在形式化定义模糊值、维模糊值及模糊OLAP查询后，可以定义维值、维层次值及单元格与概念的匹配关系。

定义4(模糊值的匹配关系=f)对于某一个确定的值dv，其与模糊值fuzzy_v 匹配，记做dv=ffuzzy_v，，当且仅当μ(dv)≥λ，即隶属度值大于阈值。

例如，对于上述的模糊值“儿童”概念，年龄值“15”与模糊值具有匹配关系(隶属度为1)，而年龄值20 则与模糊值不具有匹配关系(隶属度为0.67)。

定义5(维模糊值的隶属度ud与匹配关系=D)对于某个确定的维值dD=(dv0，dv1，…，dvk)，其与某个维模糊值的隶属度定义为:

如fuzzy_D中的某一个层次为确定值，则定义u(dvi)=1。其与fuzzy_D 匹配，记做dD=Dfuzzy_D，当且仅当μD≥min(λi)，即维模糊值的隶属度大于维中模糊值的最小阈值。

定义6(模糊OLAP查询的隶属度与匹配关系=Q)对于某个单元格cell，其与某个模糊OLAP查询fuzzy_q的隶属度定义为:

其与fuzzy_q 匹配，记做cell=Qfuzzy_q，当且仅当对于这个单元格cell所有的维值dDi，均有dDi=Dfuzzy_Di。

由上面的定义可知，某个单元格与模糊OLAP查询之间的隶属度可以通过一系列的隶属度函数进行运算得到，而单元格与模糊OLAP查询之间的匹配与否可以根据隶属度高低进行计算。

2 聚类策略选择及优化查询算法描述

2.1 聚类策略的选择

传统的聚类分析种类繁多，但由于数据挖掘的处理对象是海量的高维数据集，又有许多相适应的新聚类算法被提出，如基于网格的聚类算法，基于密度的聚类算法以及模糊聚类算法等。实际上，在数据挖掘中，特别是在模糊OLAP查询中，大多数对象并没有严格的类属性和隶属关系，它们在属性等方面存在着重叠性、交叉性，比较适合进行模糊划分，因此数据挖掘中的聚类分析主要为模糊聚类分析。

在模糊聚类分析中，主要的聚类算法是模糊C-均值算法(FCM)。FCM算法是基于对目标函数的优化基础上的一种数据聚类方法，是通过目标函数的迭代优化算法来实现对给定样品集合的划分，在本文提出的算法中采用FCM 聚类算法，其主要内容如下所述。

对于一个给定的S 维数据集x={x1，x2，…，xn}，其函数定义为:

式中，c表示分类数，n为样本数，uij表示Xj隶属到类Ci的隶属度，Vi为第i类的聚类中心，同是权重系数，d2(Xj，Vi)是样本Xj到聚类中心Vi的欧氏距离的平方。

聚类结果是每一个数据点对聚类中心的隶属程度，该隶属程度用一个数值来表示。FCM算法的主要步骤可分为:

(1)初始化聚类中心点值Vi，确定迭代停止阈值ε;

(2)计算由隶属度的值组成的划分矩阵U;

(3)利用划分矩阵更新聚类中心值;

(4)重复第2步，直至聚类中心值满足停止阈值ε的条件，则迭代停止。

由以上步骤可以看出，算法的过程就是不断地修正聚类中心值Vi和由隶属度值所组成的划分矩阵U，属于动态聚类过程。

2.2 模糊OLAP查询算法

基于模糊的聚类优化OLAP算法的详细步骤:

(1)给定数据集A={a1，a2，…，an};

(2)根据定义1 将数据集A 过滤并分成若干个“概念”子集A1，A2，…，Ap;

(3)if(数据集的维数)＞2;then 将每个高维样本的子集样本映射到二维平面，然后对得到的二维样本用FCM算法聚类;else 直接用FCM算法聚类;

(4)对p个子集聚类后分别得到的聚类中心数为m1，m2，…，mp;

(5)if|m1+m2+…+mp|＞=n0(n0为问题规模的阈值);then 将m1+m2+…+mp个聚类中心看成集合A，转到(2);else 转到第(6)。

(6)把m1+m2+…+mp个聚类中心进行一次性聚类。

(7)if 聚类中心x1和x2聚为一类，且第(4)步结束后c1和c2分别是以x1和x2为聚类中心的类;then 将类c1和c2合并为一类;else 结束。

(8)if数据集是高维样本;then 将第(7)步的聚类结果还原到原始的高维样本中;

(9)在已聚类数据中按照定义6 进行查询匹配，向用户提交查询结果。

3 实验结果与性能分析

测试所采用的数据集为TPC-R，实验是在一台Intel Pentium IV 2.6GHz，512M 内存，运行Windows 2000 Server的PC 机上执行。

实验一是采用优化方法的模糊OLAP查询执行时间与未优化查询执行时间进行对比，其结果如图1所示。由图1可以看出，由于本文提出的优化方法需要在查询时计算隶属度函数，耗费不少的CPU时间，因此在OLAP查询较少的情况下，可能执行时间比未优化的情况还要更长，但随着OLAP查询的增长，执行时间比未优化的情况显著减少。

实验二是分析模糊OLAP查询对于系统整体效率的影响，随机生成了1 000个OLAP查询，并不断提高其中模糊OLAP查询的比例，其执行时间如图2所示。

图1 优化前后执行时间对比

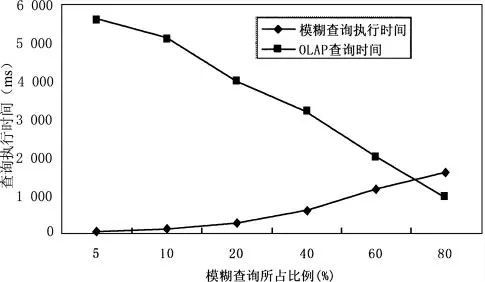
图2 不同模糊查询下执行时间对比

由图2可以看出，随着模糊查询的比例增加，总体花费的执行时间显著下降，因此在整个系统中实现对模糊OLAP查询的支持，对于整体效率的影响明显。

4 结束语

本文在对模糊OLAP查询进行形式化描述的基础上，利用模糊逻辑生成元组、单元格与模糊OLAP查询的匹配度，判断出隶属度低的元组或单元格，使其不参与聚类计算;将高维数据映射到二维平面，再用FCM算法聚类，从而减少整个查询系统的耗费代价，实验证明，本算法确实改善了系统的性能。今后的工作将继续对模糊OLAP查询的匹配度进行研究，并改进FCM算法，以进一步提高模糊OLAP查询的效率。

[1]Codd E F，Codd S B，Salley C T.Providing on-line analytical processing to user-analysts[J].An IT mandate，1993，25(3):45-49.

[2]Nigel Pendse，What is O L A P.OLAP report[EDOL].http://www.olapreport.com/about.htm，2000-03-10.

[3]Jerbi H，Ravat F，Teste O，etal.Applying recommen-dation technology in OLAP systems[C].Beijing:International Conference on Enterprise Information Systems，2009:220-233.

[4]Jerbi H，Ravat F，Teste O，etal.Management of con-text-aware preferences in multidimensional databases[C].London:International Conference on Digital Information Management，2008:669-675.

[5]孟祥福，马宗民，严丽.数据库模糊查询结果自动排序方法[J].东北大学学报(自然科学版)，2008，29(7):960-964.