一种基于偏微分方程的数值解的图像矢量化方法

(杭州电子科技大学图形图像研究所，浙江 杭州310018)

0 引 言

计算机中的图像分为两大类:栅格图像和矢量图像。矢量图像用少量的点、直线、多边形等几何图元表示，所占存储空间小，并且易于对其进行操作[1]，在现代计算机系统中得到广泛的应用。图像矢量化方法有很多，其中比较经典的矢量化方法有基于优化梯度网格的图像矢量化[2]，以及其改进方法一种拓扑保持的梯度网格表示图像的方法[3]。偏微分方法将曲面看作椭圆型偏微分方程在边界条件下的解，由于偏微分方法只需少量边界条件即可表示复杂的三维曲面，所需存储量少因而非常高效。近年来国外学者研究了采用椭圆型偏微分方程作为曲面模型，将从未知曲面提取出的轮廓线作为边界条件，通过偏微分方法拟合曲面的基本原理和应用[4]。本文在偏微分方法构造曲面的基础之上，提出了利用偏微分数值解进行图像矢量化方法，提取图像的轮廓线作为边界条件，通过求解非线性方程组，有效的将处理图形的方法来处理图像。

1 求解偏微分方程的有限差分方法

有限差分法是数值求解偏微分方程的一种有效的方法，将偏微分方程的解转化为一组代数方程方程组，容易在计算机中实现[5]。有限差分方法在节点很多的情况下将偏微分方程求解问题归结为解大型的线性方程组的问题，此时的系数矩阵常是对3 对角或块状3 对角，其中非零元素占的比例很小(称为稀疏矩阵)，分布也有一定的规律，迭代法可以比较充分地利用这些特点，因此它是解代数方程组的一种重要方法。用迭代法解方程的优点是:程序简单，对于稀疏矩阵存储量可以大为减少，而且收敛的迭代过程是一个不断修正误差的渐进过程，因此数值解的精度就相对比较高。

假设所求曲面X=X(u，v)满足如下的偏微分方程:

式中，u，v为给定的参数，及给定边界线Ci(i=0，1，2，3)，边界条件为:

采用有限差分法求解偏微分方程曲面，首先对参数区域围成的矩形网格剖分，然后把偏微分方程中的所有偏导数用它们的离散逼近采样点替换。对矩形网格区域用两组平行于坐标轴的直线ui=ih，vj=jh 进行剖分，假定给定的步长为:h=1/M，则共有M-1个内结点，在每个内结点(i，j)上，用二阶中心差分格式代替式中二阶偏导数，得到:

2 基于偏微分方程数值解的图像矢量化方法

2.1 初始边界条件

对于一幅输入的彩色图像，如图1(a)，(c)所示，为初始输入图像peeper，图1(b)，(d)为初始输入图像lemon，可以采样得到边界象素信息，然后通过B样条拟合得到初始的边界条件。本文采用的是3次均匀B样条来拟合边界曲线。

图1 初始边界条件

3次均匀B样条曲线段得矩阵表示为:

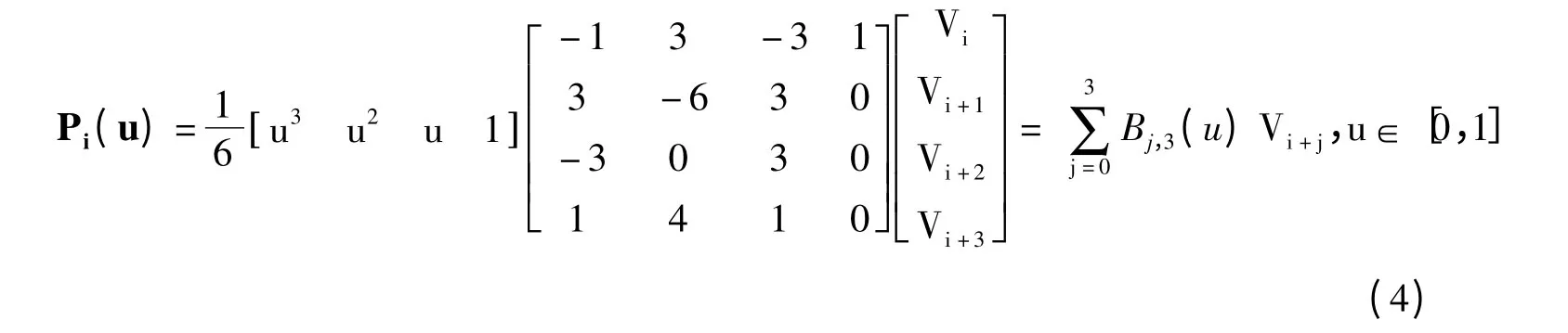
式中，Bj，3(u)，j=0，1，2，3为3次B样条基函数，Pi(u)表达式为:

以上矩阵表达式写成:A=BC。用正交方程组的形式表示:BTA=BTBC。

令BTA=E，BTB=F，C为所要求的矩阵，用X 矩阵表示，则:FX =E;其中E，F 都是已知的矩阵，可以直接求出X 矩阵，即为控制顶点矩阵。如图1(b)为图1(a)pepper 初始的边界条件。

2.2 双线性插值方法

通过双线性插值方法得到最终的输出图像如图2所示。

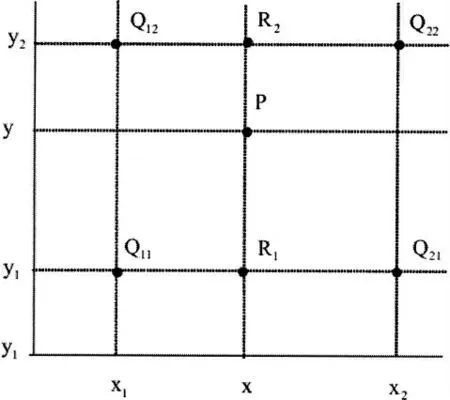
图2 双线性插值

图2中，Q11，Q12，Q21，Q22为已知点，分别在x方向和y方向进行双线性插值，得到:

图1经过双线性插值得到最终的输出图像如图3所示:

图3 双线性插值效果图

从图3可以看出通过以上步骤进行矢量化后的输出结果并不理想，最终生成的图像边界不明显，出现模糊的现象，可见此种方法对于形状以及颜色比较复杂的物体的矢量化的效果并不理想，接下来考虑一些改进的方法，可以将图像首先进行分割，然后针对每个子对象来进行矢量化。做这样的处理时，仅仅需要对图像进行预处理，分割出来的子对象的边界比较清晰，且颜色单一，矢量化的其他步骤和我们之前处理整幅图像的步骤一样。

如图4所示，图4(a)，(c)为初始输入图像，图4(b)，(d)为采用仅对子对象实现矢量化的改进方法以后的输出结果，从输出结果可以看出，做这样的处理之后的矢量化结果是比较理想的，能如实反映原始输入图像。

图4 图像分割后的处理效果图

3 结束语

偏微分方程的数值解法主要采用的是有限差分的方法，具体实现时采用5点差分的格式，得到采样点邻近象素点的信息，但是这样处理并不能得到图像上所有象素点的信息，接下来采用双线性插值的方法，将未知的象素点信息求出来，得到最终的输出图像。对于整幅图像进行这样的处理后，矢量化的效果并不理想，做了进一步的改进，只针对图像区域进行矢量化，先将图像分割，对具体的图像子对象来实现矢量化过程，得到矢量化结果。

[1]彭容杰.图像矢量化方法研究与英语[M].武汉:华中科技大学，2006:35-45.

[2]Sun J，Liang L.Image vectorization using optimized gradient meshes[J].ACM Transactions on Graphics，2007，3(11):1-7.

[3]Lai Yu-Kun，Hu Shi-Min.Automatic and Topology-Preserving Gradient Mesh Generation for Image Vectorization[J].ACM Transactions on Graphics，2009，28(3):1-7.

[4]Ugail H，Kirmani S.Shape Reconstruction using Partial Differential Equations[J].WSEAS Transactions on Computers，2006，10 (5):2 156-2 161.

[5]李瑞遐，何志庆.微分方程数值方法[M].上海:华东理工大学出版社，2005:70-76.