周期环境中尺度结构线性种群模型的适定性

(杭州电子科技大学运筹与控制研究所，浙江杭州310018)

0 引 言

对于大多数种群而言，个体的尺度指标对其生存和繁殖具有决定性作用。目前，基于尺度结构的种群模型已引起广泛关注[1]。从总体上看，研究成果还不多。主要的结果有，一类尺度结构种群模型的解的局部存在性及其对初始条件的依赖性[2];模型正解的局部存在性及全局有界性[3];种群个体由外界环境的迁入后对种群动力学行为的影响，及再生数与解的稳定性之间的关系[4];基于尺度结构的并且带有迁移项的非线性种群动力系统平衡态的存在唯一性及其稳定性[5];以及周期环境中年龄依赖的线性种群模型的动力学[6]。本文研究周期环境中具有尺度结构的线性种群模型的定性行为。

1 模型

为适应环境的季节性变化，建立如下的具有周期参数的种群模型:

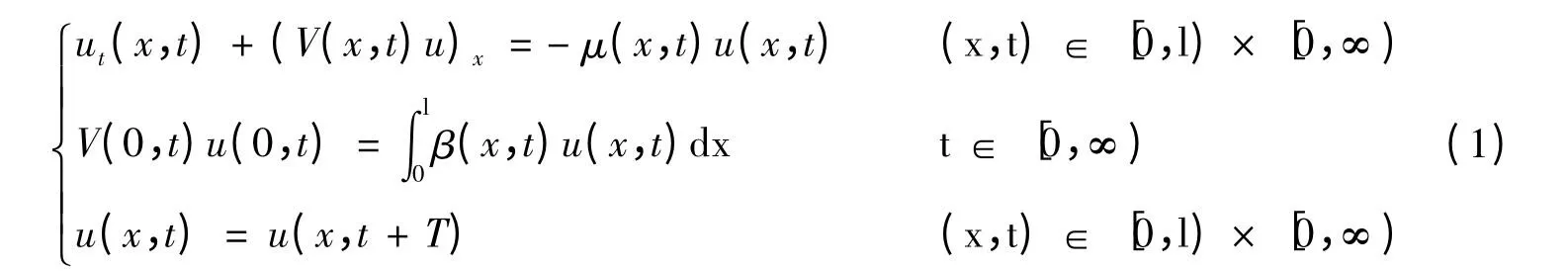
式中，u(x，t)表示t时刻尺度为x的种群个体密度;生命参数β(x，t)、μ(x，t)、V(x，t)分别表示t时刻尺度为x个体的繁殖率、死亡率和尺度增长率;常数l表示个体不能超越的最大尺度;常数T ＞0为环境变化周期。

本文采用的基本假设如下:定义Q=[0，l)×[0，∞)，(1)0≤β(x，t)为常数，且β(x，t)=其中是一个有界的连续函数，对于∀t∈[0，∞)，有V(l，t)=0 且V(x，t)关于x 满足局部Lipschitz条件，V(x，t)＞0，且V(x，t)=V(x，t+T)a.e.Q。

2 解的定义

定义1 称初始条件x(t0)=x0下，常微分方程x'(t)=V(x，t)的唯一解为通过点(t0，x0)的特征曲线，记为x=φ(t;t0，x0)。

定义3 记L∞T(Q)= {h(x，t)∈L∞(Q):h(x，t)=h(x，t+T)}，若u(x，t)∈L∞T(Q)沿着每条特征曲线φ 绝对连续，且满足:

式中，函数u(x，t)为式1的解。

注记1 由于u(x，t)沿着每条特征曲线φ 绝对连续，因此式2中的第二式是有意义的。

3 模型的适定性

记x-t 平面上通过点(0，0)的特征曲线为z(t)。对第一象限上任意固定点(x，t)，当x≤z(t)，定义其初始时刻为= (t，x)，有φ(t;，0)=x⇔φ(;t，x)=0。考虑满足式2 中第一式和第二式的函数u(x，t)。当t ＞z-1(l)时，根据定义1和定义2 知:

令σ=φ(s;t，x)，则s=φ-1(σ;t，x)，且dσ=V(φ(s;t，x)，s)ds=V(σ，φ-1(σ;t，x))ds。故由积分变量替换知:

式中，b(t)为如下Volterra 积分方程的解:

则式3 必为式1的解。

于是，总结上述分析即有下列结果:

引理1 设b(t)∈L∞T(R)是式8的解，则式5 给出的u(x，t)是式1的解。进一步，式5 解的唯一性保证了式1 解的唯一性。

现在讨论式8 解的存在唯一性。为此，对满足假设2的固定的μ，定义如下的有界线性算子，Pμ:

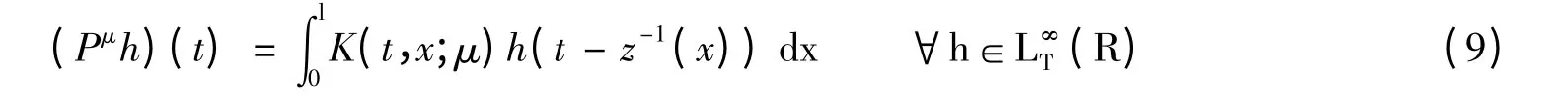
由于K(·，·;μ)∈L∞(Q)并且K(t，x;μ)=K(t+T，x;μ)a.e.(x，t)∈Q。从而式9的定义是合理的。因此式8可以写成L∞T(R)中如下的抽象方程:

定理1 记r(Pμ)为算子Pμ的谱半径，如果r(Pμ)＜1，则式10 在L∞T(R)中有唯一解。

证明 对于有界线性算子Pμ的谱σ(Pμ)={λ∈C:Pμ-λe 不可逆}，由于r(Pμ)＜1，则1∈ρ(Pμ)，即Pμ-e可逆。从而式10 在L∞T(R)中有唯一解。

定理2 假设对∀t∈R，有R0(t)＜1，则式1 有唯一的非负解

证明 由引理1 及定理1 知，若对∀t∈R，有R0(t)＜1，即可得:

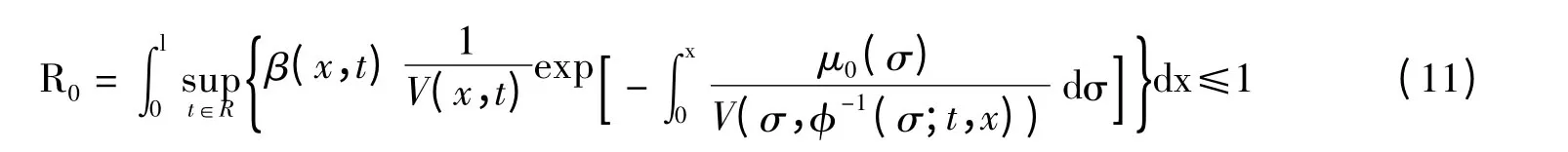
即有r(Pμ)≤R0＜1，则式1 有唯一的解u(x，t)∈L∞T(Q)。

接下来证明解u(x，t)的非负性。由于式5的解是L∞T(R)如下迭代序列的极限:

由假设1-3 知:对∀(x，t)∈Q 有K(t，x;μ)≥0，于是就有bn(t)≥0。从而就有极限b(t)≥0，于是由式5 知u(x，t)≥0。

综上所述:若∀t∈R，有R0(t)＜1，则式1 有唯一的非负解u(x，t)∈L∞T(Q)。

以下两个结果表明解关于死亡率和出生率的单调性:

定理3 设uμ(x，t)为式1 对应于μ的解，若μ1(x，t)≥μ2(x，t)a.e.(x，t)∈Q，则uμ1(x，t)≤uμ2(x，t)a.e.(x，t)∈Q。

证明 当μ1(x，t)≥μ2(x，t)a.e.(x，t)∈Q时，由式7可知:K(t，x;μ1)≤K(t，x;μ2)，从而结合式12可得:bμ1(t)≤bμ2(t)，进一步由式5可知:uμ1(x，t)≤uμ2(x，t)。

定理4 设uβ(x，t)为式1 对应于β的解，若β1(x，t)≥β2(x，t)a.e.(x，t)∈Q，则uβ1(x，t)≥uβ2(x，t)a.e.(x，t)∈Q。

证明 当β1(x，t)≥β2(x，t)a.e.(x，t)∈Q时，由式7可知:K(t，x;μ1)≥K(t，x;μ2)，从而结合式12可得:bμ1(t)≥bμ2(t)，进一步由式5可知:uβ1(x，t)≥uβ2(x，t)。

4 结束语

本文研究了一类周期环境中具有尺度结构的线性种群模型的适定性，讨论了模型的解的存在唯一性，并且给出了模型解关于出生率和死亡率的单调性。另外本文没有考虑到种群的迁移和收获，将进一步探究周期环境中含迁移项和收获项的线性模型。

[1]Tuljapurkar S，Caswell H.Structured-Population Model in Marine Terrestrial and Freshwater Systems[M].New York:Chapman＆Hall，1996:83-86.

[2]Kato N，Torikata H.Local existence for a general model of size-dependent population dynamics[J].Abstr Appl，1997，2(5):207-226.

[3]Kato N.Positive global solutions for a general model of size-dependent population dynamics[J].Abstr Appl，2004，5(4):191-206.

[4]Farkas J Z.Structured population:The stabilizing effect of an inflow of newborns form an external source and the net growth rate[J].Appl Math Comput，2008，26(4):547-558.

[5]王海涛，何泽荣，刘炎.带有Size 结构和迁移的种群系统的稳定性[J].杭州电子科技大学学报，2010，30(1):58-61.

[6]Anita S.Analysis and Control of Age-Dependent Population Dynamics[M].Dordrecht:Kluwer Academic Publisher，2000:51-56.