SMOOTHNESS INDICATOR OF WENO SCHEME FOR RESOLVING SHORT WAVE

Wu Conghai（武从海），Zhao Ning（赵宁） Xu Shuang（徐爽），Wang Donghong（王东红）

（1.College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China；2.College of Science，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China）

INTRODUCTION

Weighted essentially non-oscillatory（WENO）schemes，originally proposed by Liu，et al［1］and later improved by Jiang and Shu［2］have spread rapidly in the field of computational methods for hyperbolic conservation laws.The key idea of WENO schemes is an adaptive interpolation or reconstruction procedure. Therefore， these schemes are specially suitable for the problems containing both discontinuities and complex smooth solution features［3］.

However，numerical tests indicate that these schemes are generally not optimal for computing turbulent flows and aero-acoustic fields because they can lead to a significant damping of turbulent or acoustic fluctuations.This damping mainly acts on short waves with respect to the grid lengths which can not be ignored in turbulent flows and aero-acoustics problems.Using a high-er order WENO scheme can alleviate this problem，but the computation cost will be increased at the same time.Compact schemes could be a good choice for these problems because of its better spectral resolution property［4－6］. But these schemes often produce systems of linear equations to be solved and also need additional nonlinear treatment to tackle the problems of discontinuities.

Nevertheless，with the help of the optimized WENO schemes［7］，the error in wave number space can be minimized with assuring the order of convergence，which reduces the damping behaviour in turbulent or aero-acoustic flows.As for the smoothness indicators of WENO schemes，those developed by Jiang and Shu［2］added significant numerical damping into the schemes for short waves at about 6—8points per wavelength（PPW）.Therefore，Wang and Chen［8］proposed a series of smoothness indicators for optimized WE-NO schemes to simulate short waves with better resolution.Nevertheless，these schemes［7－8］are usually restricted to the case of r≥4，which corresponds to the WENO schemes using stencils with at least seven points［9］.

By replacing the square of the first-order term with the product of the first-order term and the third-order term，a new smoothness indicator for WENO schemes is developed using five-point stencil.Combined with the weight computing method［10］，a fifth-order WENO scheme is developed with less dissipation and better resolution for short waves.

1 TRADITIONAL FIFTH-ORDER WENO SCHEME

A scalar hyperbolic conservation law is considered

where xand t stand for space and time，respectively，u （x，t）is a conserved quantity and f （u（x，t））the flux.The considered grid is uniform，xi＝iΔx，i＝0，1，…，N，Ii＝ ［xi－1／2，xi＋1／2］，and the cell boundary is defined as xi±1／2＝xi±Δx／2.Then，the semi-discretized conservative difference scheme for Eq.（1）can be written as

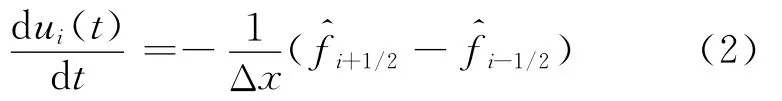
The fifth-order WENO scheme is based on a five-point stencil which is a union of three threepoint candidate stencils with an upwind bias.Forthe stencil is shown in Fig.1.As for theboth the stencil and the flux can be obtained symmetrically.For nonlinear problems，a flux-splitting procedure such as Lax-Friedrichs splitting is also needed.

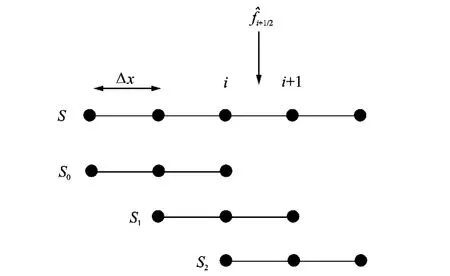
Fig.1 Stencil of fifth-order WENO scheme

The numerical flux in Eq.（2）can be written as

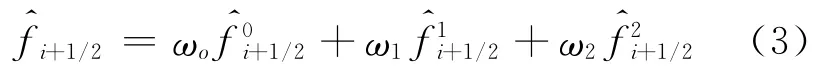
where

In this article，variant kis set as k＝0，1，2，if not specified.The parametersεand pare often set to 10－6and 2，respectively.Coefficients d0＝1／10，d1＝3／5，d2＝3／10are optimal weights，with which the fifth-order upstream central scheme is achieved.

The smoothness indicatorβ（JS）kmeasures the smoothness of the flux on the candidate stencil Skwhich is given as［2］

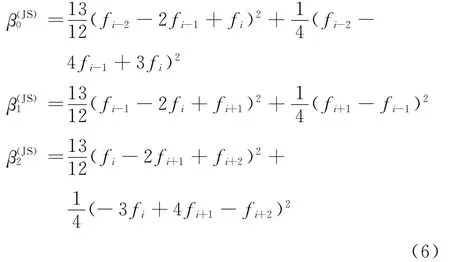
It can be written as

2 NOVEL SMOOTHNESS INDICATOR AND WENO SCHEME

Improvements on smoothness indicator of WENO schemes have been made for different problems.For the steady shock problem，Zhang and Shu［11］introduced a smoothness indicator for fifth-order WENO to improve the convergence property.Furthermore，Wang and Chen［8］proposed an alternative definition of smoothness indicators for the optimized WENO schemes on a（2r－1）-point stencil

With Eq.（8）a better resolution for short waves can be achieved.This can be attributed to that the first-order derivative of the approximate function is left out in the smoothness indicators.However，r in the smoothness indicator （Eq.（8））is restricted to r≥4，corresponding to stencils with at least seven points.For five-point（r＝3）stencil S （Fig.1），however，there is only the second-order derivative in this smoothness indicator，which will cause instability in numerical experiments.

On the other hand，the Taylor expansion can be used to analyze the smoothness indicator（Eq.（6））in smooth region.Since the major parts of Akand Bkare f″2iΔx4and 4f′2iΔx2，respectively，the order of Akis higher than that of Bkby two，which means that Akis much smaller than Bkin the smooth region.To match the order of these two terms and to decrease effect of the first-order derivative，we consider a smoothness indicator in the form

where mis used to adjust the proportions of two terms.The expression ofβ（Q）kused in this work is

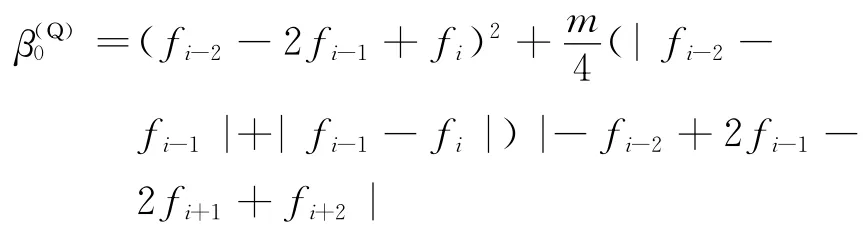
Since the approximations of the third-order are not available for three-point candidate stencils，the data on the whole stencil can be used.As a result，the differences among smoothness indicators of candidate stencils can be reduced.Therefore，the weights will be even closer to optimal weights，and the resolution will be improved while some stability is sacrificed.

The sufficient condition for WENO scheme achieving fifth-order accuracy is［2］

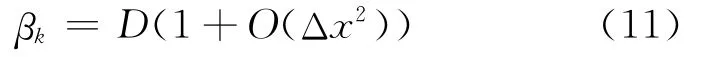
where Dis some nonzero quantity.In fact，this condition comes from

However，the new smoothness indicator cannot satisfy the condition（Eq.（11）），and the final WENO scheme with this smoothness indicator only has a convergence rate of fourth-order.Fortunately，Borges，et al［10］introduced a different way to compute the weights of WENO schemes which avoids the restriction of condition （Eq.（11））.Hence，this technique is combined with the novel smoothness indicator to preserve the fifth-order accuracy of WENO scheme.In this

Therefore，the accuracy requirement is put onConsidering accuracy，different from the original form［12］，τis defined as

And the final weights are

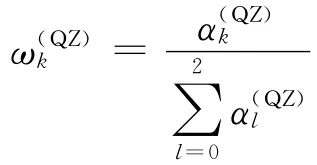
whereε＝10－40avoids zero denominator，and integer penlarges the differences among the weights on the candidate stencils，which is often set to 2.

In smooth region，after Taylor expansion，we can have

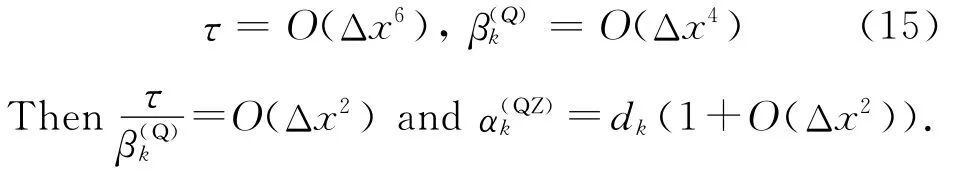
As a result，the condition（Eq.（15））is satisfied.Therefore，the new WENO scheme can achieve fifth-order accuracy for smooth problem.

Since the formulas Eqs.（13－14）are different from those in Refs.［2，12］，the time efficiency of the resultant scheme is not the same as the former ones.According to our numerical tests，the fifth-order WENO scheme using the new smoothness indicator consumes roughly 10%more CPU time than those schemes using previous ones for linear problems.As for Euler equations，this difference on CPU time is reduced to only about 3%.

As for the parameter m，according to a large number of numerical tests，m＝0.28shows proper numerical viscosity and preferable resolution on short waves.Therefore，it is the choice of the present work.

3 TEST ON CONVERGENCE RATE

The fifth-order accuracy of the new WENO scheme，abbreviated as WENO-Q here，is validated.The tested problem is

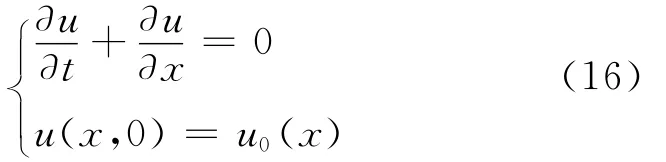
The computational domain is－1≤x≤1and periodic boundary condition is implemented.The initial conditions is u0（x）＝sin（πx）and the end of simulation time t is set to 1.The third-order TVD Runge-Kutta method［12］is employed as time integration with time stepΔt—（Δx）5／3.Therefore，the time accuracy is effectively fifth-order.The L1，L∞errors and the corresponding orders of accuracy are shown in Table 1.Obviously，the WENO-Q scheme has achieved the designed fifthorder accuracy.

Table 1 Convergence rate test for linear advection equation（u0（x）＝sin（πx））

4 NUMERICAL RESULTS

In this section，two numerical tests are taken to verify the advantage of the proposed WENO scheme.For comparison，the fifth-order WENO scheme in Refs.［2，10］and the fifth-order upstream central scheme are also tested，named as WENO-JS， WENO-Z and UP5，respectively.The third-order TVD Runge-Kutta method［11］is employed as the time integration approach.

4.1 Linear advection equation

To validate the ability of WENO-Q scheme for capturing the short waves，which is important for tackling the small-scale flow structure，the problem （Eq.（16））with a periodic initial profile u0（x）＝sin（πx／4）is tested.The computational domain is［－16，16］and the periodic boundary condition is implemented.The grid length is Δx＝1which means 8points per wave.The Courant number is set to 0.1and the end of simulation time here is t＝80.The result is shown in Fig.2with the exact solution displayed by solid line.From Fig.2，it can be found that the result of WENO-Q shows the best behavior，since it is almost the same as the exact solution.It is a little surprised that UP5does not perform best，which implies there may be some optimization in wave number space for the proposed smoothness indicator just like those in Ref.［8］.

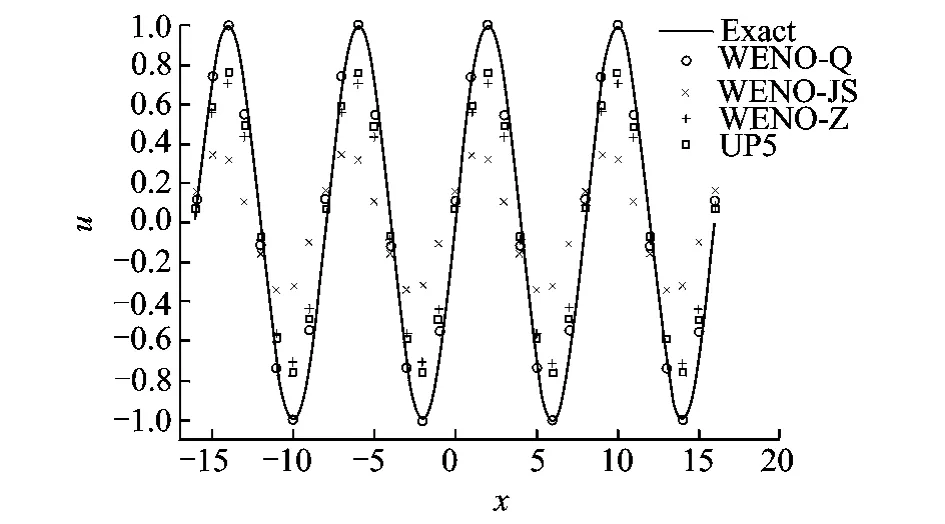
Fig.2 Single sine wave（N＝32，t＝80）

4.2 Shock-entropy wave interaction

This test case is taken from Ref.［2］，and also called Shu-Osher problem.The governing equations are the one-dimensional Euler equations with the initial conditions

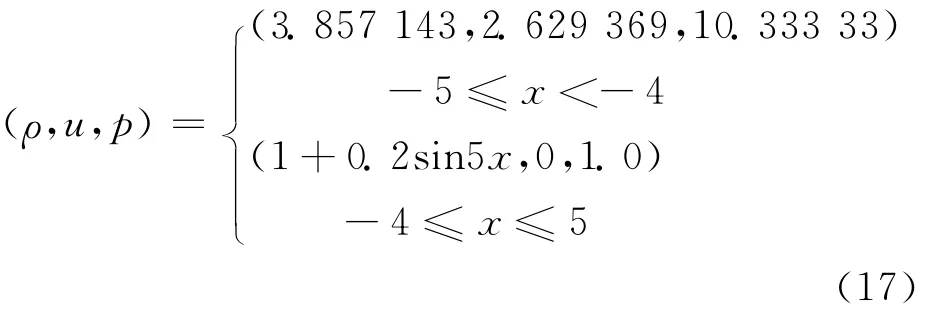
As recommended by Balsara and Shu［9］，the local lax-Friedrichs （LLF）splitting is used for linearly degenerate characteristic fields and the Roe splitting with entropy fix（RF）is used for the genuinely nonlinear characteristic fields. The densities of the results at t＝1.8with N ＝250 grid points are plotted in Figs.3－4.The solid lines in the figures mean″exact solution″attained by WENO-JS with 4 000node points since the real exact solution is not known for this problem.From Figs.3－4，it can be seen that there is no obvious difference among these results except in the″blow-up″region，downstream of the shock.In this region，WENO-JS scheme shows much viscosity in predicting post shock entropy waves at this grid resolution，while WENO-Z gets a better resolution， and the wave profile of WENO-Q is the one most close to the″exact solution″.Obviously，for this entropy wave problem，WENO-Q demonstrates advantage in comparison for its low dissipation and high resolution.

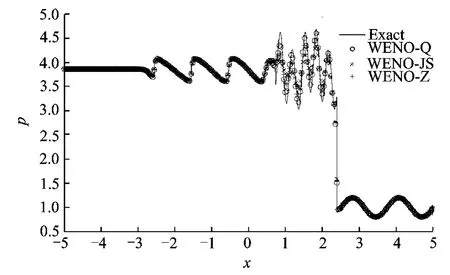
Fig.3 Shock-entropy wave interaction with density（N＝250，t＝1.8）

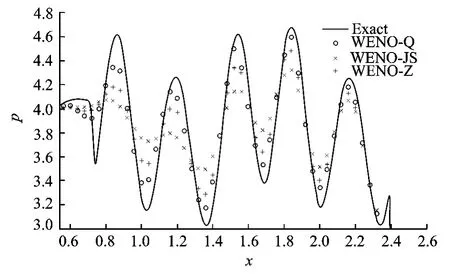
Fig.4 Enlarged portion of Fig.3downstream of shock

4.3 Shock vortex interaction

This test case is also taken from Ref.［2］which describes the interaction between a stationary shock and a vortex.The computational domain is［0，2］×［0，1］.A stationary Mach 1.1 shock is positioned at x＝0.5and normal to the x-axis.The left state is（ρ，u，v，p）＝（1，1.1γ，0，1）.A small vortex is superposed to the flow left to the shock and centers at（xc，yc）＝（0.25，0.5）.This vortex can be described as a perturbation to the velocity（u，v），temperature T＝p／ρ，and entropy S＝ln（p／ργ）of the mean flow and it is denoted by the tilde values

A uniform grid of 200×100is employed and WENO-Z and WENO-Q are tested here.The pressure contours of the results at t＝0.6are plotted in Fig.5.In Fig.5，each of the two sub-figures has ninety contours ranged from 1.19—1.37.From Figs.5（a－b），the results give approximately the same resolution.Carefully compared with WENO-Z，WENO-Q generates more numerical noise and gives a slightly thinner shock profile，which should be the result of its smaller numerical viscosity.

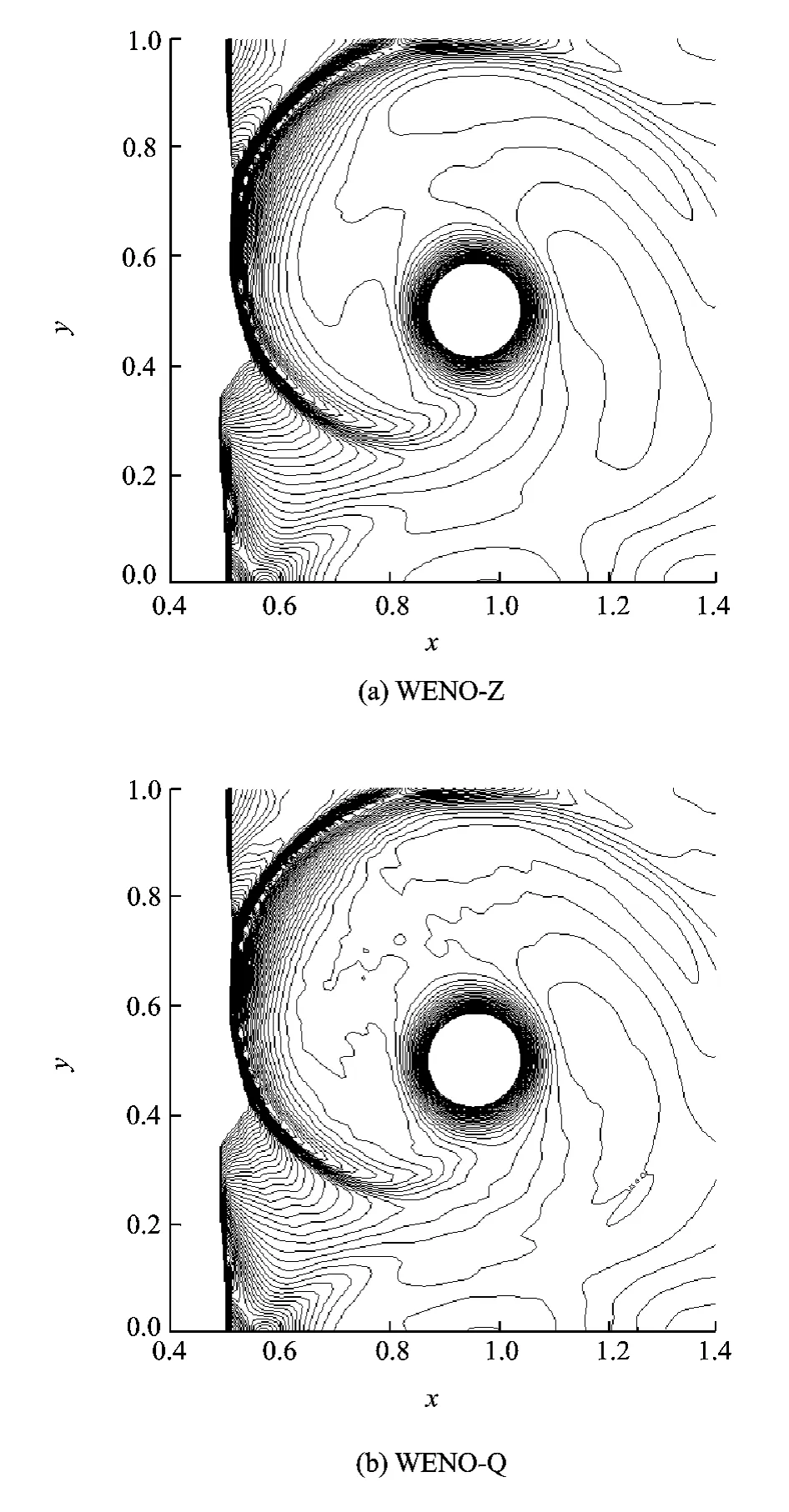
Fig.5 Shock vortex interaction with pressure contours 1.19—1.37（t＝0.6）

5 CONCLUSION

In the presented study，a novel fifth-order WENO scheme with an improved resolution on short waves is developed by using aproposed smoothness indicator.It is implemented through replacing the square of the first-order term in traditional smoothness indicator with the product of the first-order term and the third-order term.As the proportion of the first-order term is decreased，the high resolution can be achieved with a little bit of loss of stability.To preserve the fifth-order of convergence rate，the method of Borges，et al［10］is combined with this smoothness indicator.

The accuracy test shows that the aim of the fifth-order accuracy of the developed WENO scheme is achieved.Compared to the previous fifth-order WENO schemes，this scheme consumes about 10%more CPU times for linear problems and about 3%more for Euler equations，which means the increase of computing cost is relatively small.Furthermore，the numerical results show that this scheme has a better capability for resolving short waves than the previous ones，which can not be ignored in turbulent flows and aero-acoustics problems.Therefore，the proposed WENO scheme can be a better choice for these problems.

The idea of constructing the proposed smoothness indicator can be extended to the higher-order WENO schemes. Since Wang and Chen［8］has already proposed a series of smoothness indicators for these schemes，there should be a comparison of these two kinds of smoothness indicators.This will be presented in a future work.

Acknowledgements

We appreciate Dr.Zhu Jun′s helpful suggestions.

［1］ Liu X D，Osher S，Chan T.Weighted essentially non-oscillatory schemes［J］.J Comput Phys，1994，115（1）：200-212.

［2］ Jiang G S，Shu C W.Efficient implementation of weighted ENO schemes［J］.J Comput Phys，1996，126（1）：202-228.

［3］ Shu C W.High order weighted essentially nonoscillatory schemes for convection dominated problems［J］.SIAM Rev，2009，51（1）：82-126.

［4］ Lele S K.Compact finite difference schemes with spectral-like resolution ［J］.J Comput Phys，1992，103（1）：16-42.

［5］ Zhou Q，Yao Z，He F，et al.A new family of highorder compact upwind difference schemes with good spectral resolution［J］.J Comput Phys，2007，227（2）：1306-1339.

［6］ Chen L，Tang D.Study on turbulent spots in plane Couette flow［J］.Transactions of Nanjing University of Aeronautics ＆ Astronautics，2007，24（3）：211-217.

［7］ Weirs V G，Candler G V.Optimization of weighted ENO schemes for DNS of compressible turbulence［R］.AIAA-97-1940，1997.

［8］ Wang Z J，Chen R F.Optimized weighted essentially non-oscillatory schemes for linear waves with discon-tinuity［J］.J Comput Phys，2001，174（1）：381-404.

［9］ Balsara D S，Shu C W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy［J］.J Comput Phys，2000，160（2）：405-452.

［10］Borges R，Carmona M，Costa B，et al.An improved weighted essentially nonoscillatory scheme for hyperbolic conservation laws［J］.J Comput Phys，2008，227（6）：3192-3211.

［11］Zhang S H，Shu C W.A new smoothness indicator for the WENO schemes and its effect on the convergence to steady state［J］.J Sci Comp，2007，31（1／2）：273-305.

［12］Shu C W.Total-variation-diminishing time discretizations［J］.SIAM J Sci Stat Comput，1988，9（6）：1073-1084.