基于接收信号DOA估计的GPS欺骗式干扰信号识别技术

史文森，朱 海，蔡 鹏

(海军潜艇学院 航海观通系，山东 青岛266042)

0 引 言

欺骗式干扰的形式有自主产生式干扰和转发式干扰，其干扰信号的形式与GPS 信号相同或相似。GPS 接收机接收到欺骗式干扰信号后，将会解得错误的卫星位置信息和错误的伪距信息，从而解算出较大误差的定位结果［1-3］。抑制欺骗式干扰的关键在于识别接收到的信号是否为欺骗式干扰信号。若识别出接收机中某一捕获、跟踪环路中的信号为欺骗式干扰信号，接收机可以直接放弃对此信号的跟踪和解扩，使其不能参与到定位方程的解算中，从而消除其影响。目前，对欺骗式干扰信号的识别技术主要有接收机惯性补偿滤波技术、组合导航技术以及分析信号的时频域特性等。文献［4-5］利用OEM 板输出的载噪比信息，通过模糊聚类的方法，识别欺骗干扰的存在。文献［6］利用GPS 接收机获得某信号的伪距及其接收机的高程信息来识别该信号是否为欺骗式干扰。当欺骗式干扰源发射的信号有较高的信噪比，仿真度高，同一干扰源发射多个干扰信号时，上述识别欺骗式干扰方法的性能将严重下降，甚至不能识别出干扰信号。

本文利用接收机的推算位置及接收信号的DOA估计值，给出欺骗式干扰信号的识别方法。

1 欺骗式干扰信号的预识别

1.1 GPS 卫星在测者坐标系中的方向

利用卫星星历参数或接收机中预存的历书，可以得到卫星在WGS 84 中的位置为(xS，yS，zS)。假设接收机的真实位置为(λU，φU)，其在WGS 84 中的坐标为(xU，yU，zU)。而接收机在进行定位前的推算位置为(λ′U，φ′U)，其在WGS 84 中的坐标 为(x′U，y′U，z′U)。

GPS 卫星与接收机之间的位置差为:

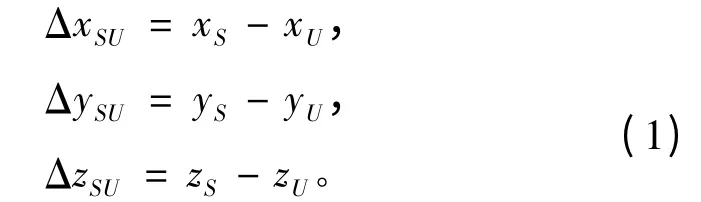
为计算卫星相对于接收机的方向，需要将WGS 84 中GPS 卫星的坐标转换到观测点所在的站心坐标系中。其变换关系为

其中:Δe 为东向距离;Δn 为北向距离;Δu 为高度差。

图1 推算舰位与真实舰位所对应的卫星方向Fig.1 The direction of GPS satellite in dead reckoning and real position

从而可得到GPS 卫星在测者坐标系中的方向b(θ，φ)为:

同理，根据推算舰位计算得到GPS 卫星在测者坐标系中的方向b(θ′，φ′)。

在GPS 卫星的方向b(θ，φ)和b(θ′，φ′)上取单位向量，可得:

由推算舰位得到的GPS 卫星方向与真实舰位得到的GPS 卫星方向之间的夹角为

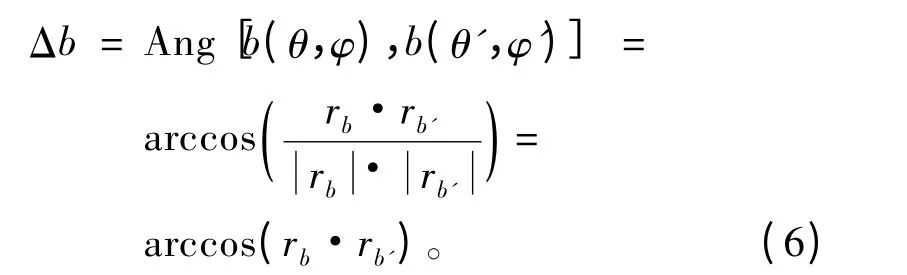
此夹角是由推算舰位误差引起的GPS 卫星方向的估计误差。

1.2 欺骗式干扰信号的预识别方法

假设空间中有2 个信号源P1和P2，其播发的信号分别为s1和s2。2 个信号源中P1的位置已知，可以计算出信号源P1的方向，记为b(θ1，φ1)，P2的位置未知。接收机测得2 个信号的DOA 分别为a(θ1，φ1)和a(θ2，φ2)，其中a(θ1，φ1)≠a(θ2，φ2)。在测者坐标系中，2 个信号方向上的单位向量可表示为:

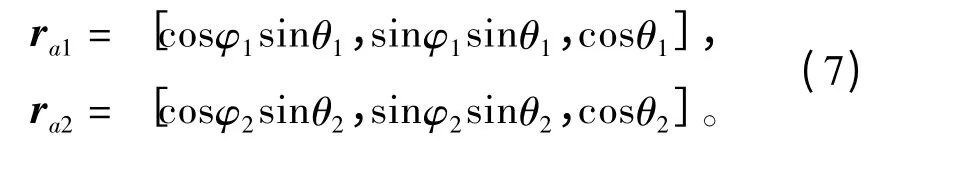
2 个信号传播方向之间的夹角可表示为

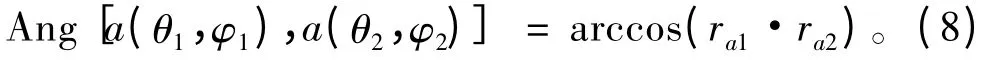
若已知准确的接收机位置且2 个信号的DOA 测量值没有误差，可得

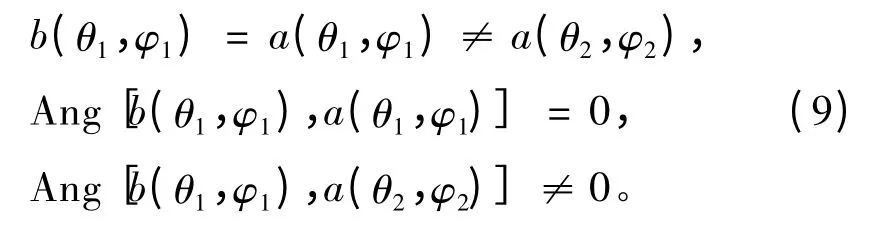
从而可以利用信号在空间中的信息确定出接收信号s1是由信号源P1发射的，而信号s2不是由信号源P1发射的。

由于接收机的推算位置存在误差，致使信号源P1方向的估计值也存在误差。信号s1的DOA 与信号源P1方向之间的夹角不再为0，其夹角的大小为信号源P1方向估计值的误差。因此，可以给出信号源P1方向的误差的最大值bΔ，当信号s1的DOA 与信号源P1方向之间的夹角小于bΔ时，可以认为信号s1是由信号源P1发射的。

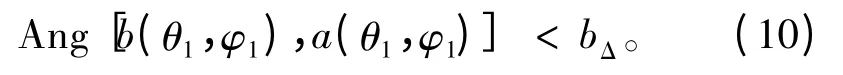
由于信号的DOA 估计值也存在误差，它对信号的识别有一定的影响。因此，可以设定1 个欺骗式干扰信号的DOA 检测门限，该DOA 检测门限的大小为信号源方向估计误差的最大值与信号DOA 估计的误差限之和，可表示为

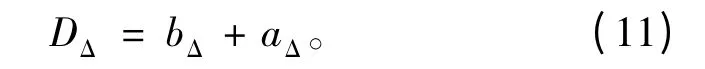
其中:bΔ为信号源方向估计误差的最大值;aΔ为信号DOA 估计的误差限。

若信号源P2所发信号s2的DOA 与信号源P1的方向之间的夹角大于欺骗式干扰信号的DOA 检测门限，即

则可认为该信号不是由信号源P1发射的。

通过上述分析，本文提出一种利用接收信号的DOA 来识别欺骗式干扰信号的方法。其过程如下:

1)首先利用阵列天线测得各GPS 信号的DOA为a(θa，φa);

2)利用接收机的推算位置和GPS 卫星的位置计算GPS 卫星在测者坐标系中的方向b(θb，φb);

3)根据接收机推算位置的误差范围，获得欺骗式干扰信号的DOA 检测门限DΔ;

4)计算接收信号的DOA 与其GPS 卫星方向之间的夹角:

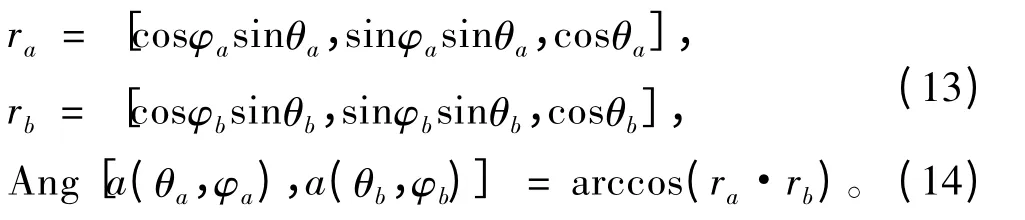
5)判断夹角Ang［a(θa，φa)，a(θb，φb)］是否大于给定欺骗式干扰信号的DOA 检测门限DΔ。

若:

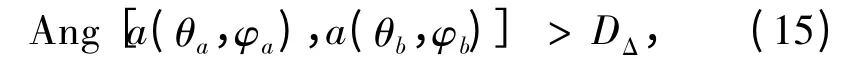
则，此信号为干扰信号;

6)若多个不同编码的信号对应于同一个DOA估计值，则该DOA 方向上的信号均为干扰信号;

7)若同一编码形式的信号来自于不同的方向，且各信号的DOA 与其GPS 卫星方向之间的夹角Ang［a(θa，φa)，a(θb，φb)］小于欺骗式干扰信号的DOA 检测门限DΔ，则此方向上存在干扰信号，可将此方向的信号放弃;

8)至此可以去除欺骗式干扰信号。

在上述过程中，步骤7 中情形出现的概率较小。为进一步提高识别欺骗式干扰信号的能力，降低步骤7 中情形出现的概率，需要提高推算舰位的精度。

1.3 欺骗式干扰信号的DOA 检测门限

GPS 卫星方向的估计误差与信号的DOA 估计误差共同决定了接收机在空域中识别信号的能力。当2 个信号的DOA 估什值之差小于GPS 卫星方向的估计误差与信号的DOA 估计误差之和时，接收机无法识别出两信号分别属于哪颗卫星。通过上节的分析可知，GPS卫星方向的估计误差与推算舰位误差的大小、推算舰位的经纬度、卫星的位置等因素有关，其中推算舰位误差是GPS 卫星方向估计误差的主要来源。GPS 卫星方向估计误差的解析表达式较为复杂，所以本文通过仿真分析的形式给出GPS 卫星方向的估计误差，并以此确定欺骗式干扰信号的DOA 检测门限。

在仿真分析中，设接收机的位置为(120°E，30°N)，而卫星位置的变化范围为:①纬度变化范围为φ ∈(10°S，70°N);②经度变化范围为φ ∈(80°E，160°E);③卫星高度为20 200 km。

当接收机推算位置的经度误差和纬度误差由0变到20 n mile 时，可以得到欺骗式干扰信号的DOA检测门限的变化，如图2所示。

从图2 可看出，欺骗式干扰信号的DOA 检测门限与接收机推算位置误差之间有线性关系。为了提高接收机在空域中识别信号的能力，降低欺骗式干扰信号的DOA 检测门限，需要减小接收机推算位置的误差。为此本文提出了接收机快速定位方法。

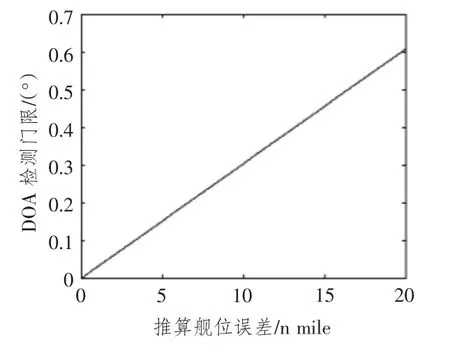
图2 DOA 检测门限随推算位置误差的变化Fig.2 The DOA detection threshold changing with the error of dead reckoning

2 基于接收机快速定位的欺骗式干扰信号的预识别方法

为提高接收机在空域中识别信号的能力，降低欺骗式干扰信号的DOA 检测门限，需要减小接收机推算位置的误差。为此本文提出了接收机快速定位方法。

2.1 接收机快速定位模型

设4 颗卫星在WGS 84 中的坐标分别为:

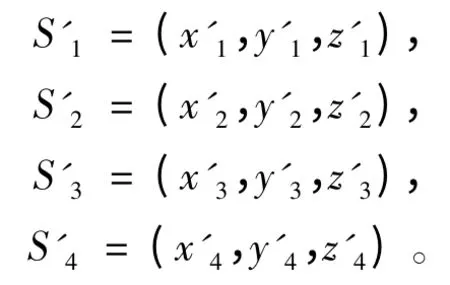
接收机在WGS 84 中的真实位置为U=(xu，yu，zu)，而接收机的推算位置为U′=(x′u，y′u，z′u)。由卫星的位置S′1，S′2，S′3，S′4和接收机推算位置U′ 可得各GPS 卫星信号的DOA 为:

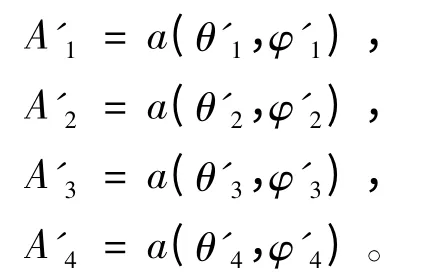
由阵列天线测得各卫星信号相对于坐标系的DOA 分别为:

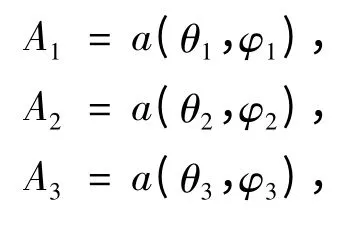
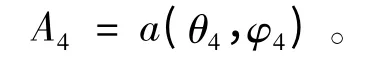
当接收机的推算位置与真实位置相差较小时，各GPS 定位信号的DOA 测量值与估算值之间的差异也较小，反之亦然。当DOA 的测量值与估算值之间的误差之和最小时，接收机的推算位置与真实位置之间的误差较小。于是，以DOA 的测量值与估算值之间的误差之和为目标函数建立接收机快速定位模型。而DOA 的估算值制约于接收机的推算位置与GPS 卫星之间的关系，并由此得到目标函数的约束条件。从而可得接收机快速定位模型为:

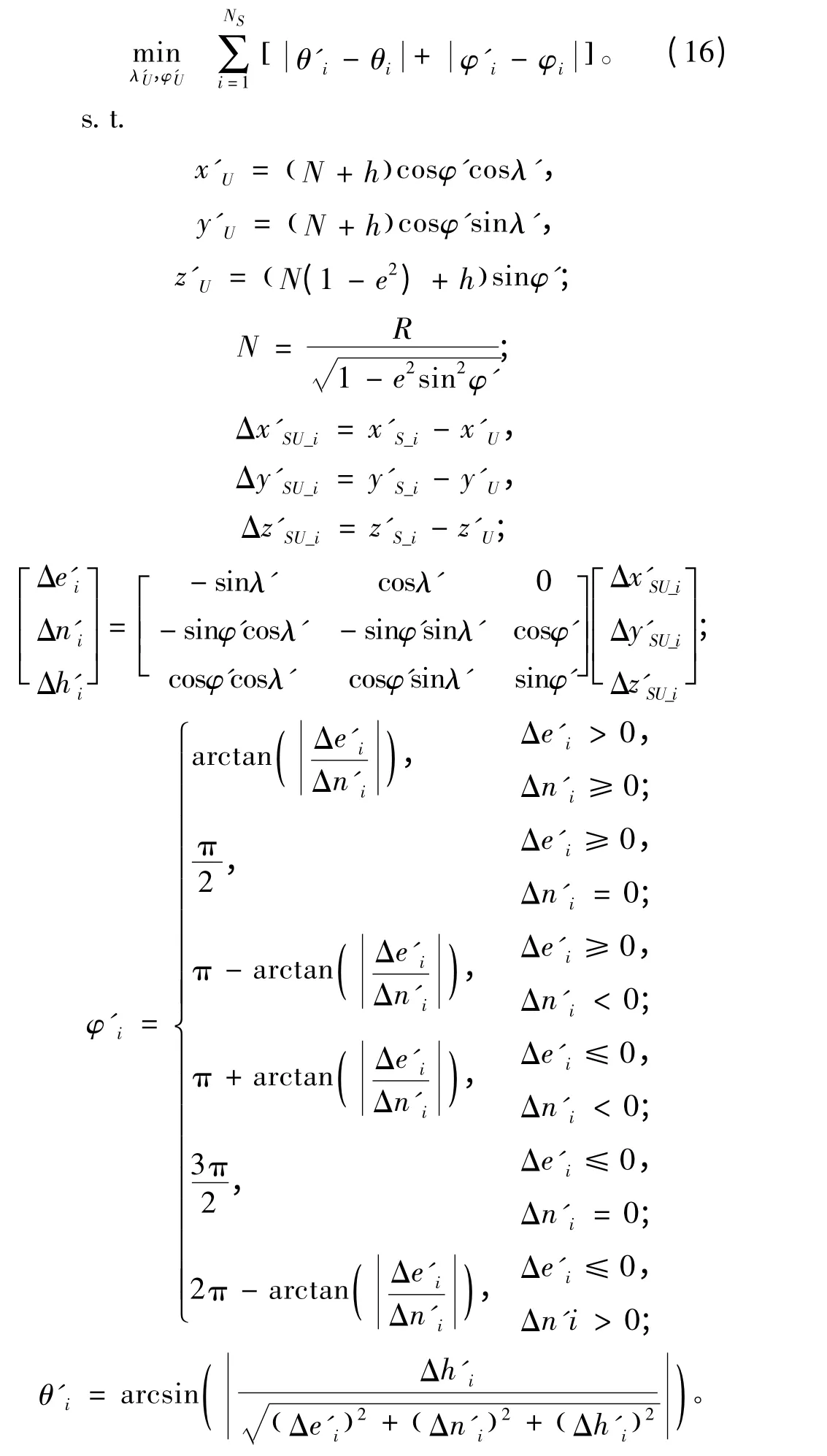
在GPS 信号的DOA 估计中得到的天顶角和方位角的误差通常小于2′，并假设其服从均匀分布，而卫星的位置误差(由历书计算得到)小于2 km，并假设其服从均匀分布。以此为条件进行300 次仿真实验，得到的定位结果如图3所示。

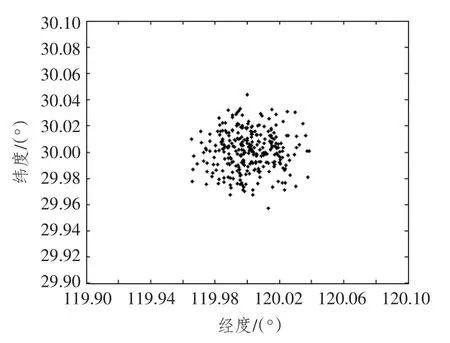
图3 定位结果仿真图Fig.3 The positions of simulation

从图3 可看出，定位结果中有99.9%集中在经度为119.96E ～120.04E (误差为2.4 n mile)，纬度为29.96N ～30.04N (误差为2.4 n mile)的范围内;定位结果中有67.8%集中在经度为119.98E ～120.02E (误差为1.2 n mile)，纬度为29.98N ～30.02N (误差为1.2 n mile)的范围内。

根据接收机快速定位方法得到接收机的概略位置后，可以得到较小的DOA 检测阈值，从而提高欺骗式干扰信号识别的能力。

2.2 欺骗式干扰信号DOA 检测门限的确定

从上述分析可看出，接收机的推算位置直接决定了欺骗式干扰信号DOA 检测门限的确定。当接收机推算位置的误差较大时，DOA 检测门限也越大，这不利于欺骗式干扰信号的识别。当2 个信号的DOA 相近时，较大的DOA 检测门限不能在空域中区分2 个信号。

基于接收机快速定位方法的定位误差范围为2.4 n mile，与推算位置的误差范围相比有了一定的降低。通过仿真分析可给出GPS 卫星方向的估计误差，并以此确定欺骗式干扰信号的DOA 检测门限。当经度误差和纬度误差均为2.4 n mile 时，GPS 卫星方向估计误差的最大为0.074°。保守起见，可令欺骗式干扰信号的DOA 检测门限为DΔ=0.1° 。

2.3 欺骗式干扰信号的识别方法

利用接收机快速定位方法得到接收机的概略位置后，可以降低欺骗式干扰信号的DOA 检测门限，从而识别欺骗式干扰信号的能力。

利用接收信号的DOA 来识别欺骗式干扰信号方法中完整的过程有以下10 个步骤:

1)首先利用阵列天线测得各GPS 信号的DOA为a(θa，φa);

2)利用接收机的推算位置和GPS 卫星的位置计算GPS 卫星在测者坐标系中的方向b(θb，φb);

3)根据接收机推算位置的误差范围，获得欺骗式干扰信号的DOA 检测门限DΔ;

4)计算接收信号的DOA 与其GPS 卫星方向之间的夹角:

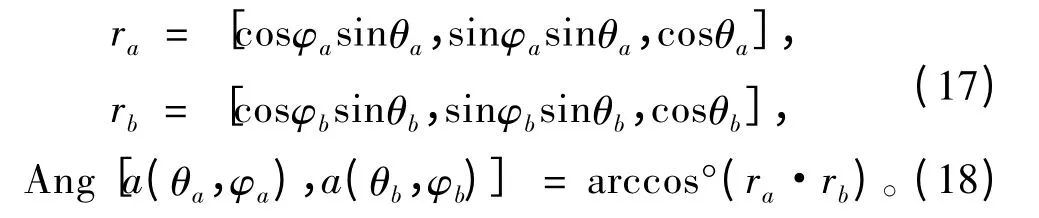
5)判断夹角Ang［a(θa，φa)，a(θb，φb)］是否大于给定欺骗式干扰信号的DOA 检测门限DΔ。若

Ang［a(θa，φa)，a(θb，φb)］＞DΔ，

则此信号为干扰信号;

6)若多个不同编码的信号对应于同1 个DOA估计值，则该DOA 方向上的信号均为干扰信号;

7)若同一编码形式的信号来自于不同的方向，且各信号的DOA 与其GPS 卫星方向之间的夹角Ang［a(θa，φa)，a(θb，φb)］小于欺骗式干扰信号的DOA 检测门限DΔ。则此方向上存在干扰信号，可将此方向的信号放弃;

8)将剩余GPS 信号的DOA 应用于接收机快速定位方法，得到接收机的概略位置，重新计算GPS卫星在测者坐标系中的方向b(θb，φb);

9)根据接收机快速定位方法的定位精度，重新给出一个较小的欺骗式干扰信号的DOA 检测门限DΔ;

10)然后依次进行步骤4 ～步骤7 可去除欺骗式干扰信号。

值得指出的是，在上述过程中，步骤7 中情形出现的概率已经非常小，它相当于GPS 卫星、干扰源和接收机几乎在同一条直线上。

3 仿真分析

接收机利用阵列天线接收到5 颗GPS 卫星所发出的信号，并得到GPS 卫星相对于接收机的方向，如表1所示。

表1 各GPS 卫星的方向Tab.1 The direction of GPS satellites

设接收机受到欺骗式干扰，若欺骗式干扰源位于地表，则其信号DOA 中的天顶角约为90°。可以看出，欺骗式干扰信号与GPS 卫星信号来向的夹角远大于1°，可以直接做出识别。

若干扰源利用飞行器布放在空中，利用本文提出的方法对信号进行识别时可能会有一定的影响。设干扰源相对于接收机的方向服从均匀分布，天顶角θ ∈(5°，90°)，方位角φ ∈［0，360°)。利用蒙特卡罗方法进行105次试验，其仿真结果如图4所示。

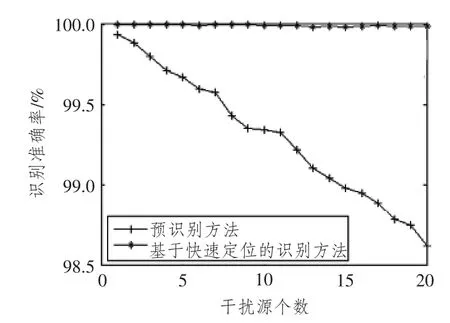
图4 干扰信号识别的成功率Fig.4 The success rate of deception jamming identification

利用欺骗式干扰信号的预识别方法时，由于接收机的推算误差较大，致使DOA 识别门限较大，当干扰源和卫星相对于接收机的方向差别不大时，该方向上的卫星信号也将被认为是干扰信号而被去除。从图4 可看出，当干扰源的数量较多时，欺骗式干扰信号的预识别方法识别信号的准确率下降明显。利用接收机快速定位算法得到接收机的概略位置后，可以提高对信号进行识别准确率。

4 结 语

本文利用GPS 信号和欺骗式干扰信号在空域的分布特征，提出GPS 欺骗式干扰信号识别技术。该技术具有以下特点:识别信号的能力较强、需要信号的数据量小，无需求解信号的伪距等。

［1］PRICE B，JETTON J.Selective GPS jamming［C］.ION GPS.2000.2096-2104.

［2］HOLLAND R L.GPS in the range of navigation war［J］.Armada Tnternational，1999，18(5):225-267.

［3］SUN W，MOENESS G A.A self-coherence anti-jamming GPS receiver［J］.IEEE Transactions on Signal Processing.2005，53(10):3910-3915.

［4］刘延斌，苏五星，闫抒升.转发式欺骗信号干扰GPS 接收机的效能分析［J］.空军雷达学院学报，2004，18(4):4-7.

LIU Yan-bin，SU Wu-xing，YAN Shu-sheng.Efficiency analysis of repeater deception jamming GPS repeater［J］.Journal of Air Force Radar Academy，2004，18(4):4-7.

［5］陈必然，徐彬.一种GPS 欺骗干扰的判断算法［J］.光电工程，2009，36(12):119-122.

CHEN Bi-ran，XU Bin.A judging method of GPS spoofing interference［J］.Opto-Electronic Engineering，2009，36(12):119-122.

［6］王琼，王伟，戚宗峰.欺骗干扰条件下的GPS 定位方程求解性能研究［J］.航天电子对抗，2008，24(2):21-23.

WANG Qong，WANG Wei，QI Zong-feng.Solution performance of GPS positioning equation under the condition of deception jamming［J］.Aerospace Electronic Warfare，2008，24(2):21-23.

［7］WARD P W.GPS receiver RF interference monitoring［J］.Mitigation and Analysis Techniques，1995，41(4):1542-1552.