聚碳酸酯熔体挤压流变研究
2013-12-01王韬,曹伟,颜悦,厉蕾
王 韬,曹 伟,颜 悦,厉 蕾
(1北京航空材料研究院,北京100095;2郑州大学 橡塑模具工程中心,郑州450002)
在聚合物注射压缩成型[1-3]和发泡成型[4]等加工过程中,聚合物熔体由于模具型腔的变化或者外来气压的作用而发生不同程度的挤压流动,挤压流动表面上类似于拉伸流动的逆过程,但实际上是混合了剪切与拉伸的复杂流动,其流变行为与拉伸流动截然不同。
为了研究流体在挤压过程中的流变规律,国内外学者开展了大量的理论及实验研究。Laun等[5]应用幂律模型推导出在恒定体积下熔体轴向挤压力的解析式,建立了挤压应力与流体性能、平板间距及平板挤压速率之间的关系。在此基础上,Ran等[6]应用同伦分析法求解挤压流动过程,得到级数形式的挤压应力解析解。Meeten[7]研究了一系列结构流体恒力挤压过程中的流变学行为,发现平板间距都会随挤压速率的降低而达到一个稳定值。Chan等[8]用挤压式流变仪评价了黏塑性流体黏度模型的适用性,发现Herschel-Bulkley模型最能代表黏塑性材料在挤压下的流变学行为,同时实验结果显示当挤压速率小于2.4mm/s时不发生壁面滑移现象。
随着计算流体力学的发展,对挤压流动过程的数值模拟也日益活跃起来。Debbaut[9]应用有限元方法研究了恒定体积流体在两个无限长平板间挤压流动过程,分析了温度边界层的发展及流体黏弹效应,同时研究了恒速下挤压应力的发展变化。Karapetsas等[10]结合有限元与准椭圆网格划分技术研究了黏塑性材料在平板间被挤压以及被挤出时的流动特点,发现在恒力和恒速下两种方式均可准确预测出流体的屈服应力。
聚碳酸酯(Polycarbonate,PC)因其透明、耐热等优点广泛应用于光学透镜、激光唱片、航空透明件、汽车车窗等高性能光学制品领域,为减小制品残余应力,提高制品性能,常用注射压缩技术来加工PC制品,而压缩过程存在明显的熔体挤压流动。研究PC熔体的挤压流变行为有助于了解PC制品加工问题,掌握成型技术,提高制品加工效率。然而,国内外针对PC的挤压流变研究较少,将其他材料模型应用于PC挤压过程预测时,其结果与实验有很大差异。因此,本工作开展了PC挤压过程的实验研究,并探索适当的本构模型描述PC挤压过程的流变行为,为真实制品的成型数值仿真提供理论依据。
1 实验设计
本实验基于ARES-G2流变仪设计了恒定接触面积挤压设备,如图1所示。上下两个圆形平板a和b同轴,圆板的直径均为25mm。上圆板a通过刚性支撑柱c与力/位移传感器d相连接,传感器信号经过A/D转换在监控系统f上实时显示。由于聚碳酸酯易吸水,特别是在高温下极易发生吸水降解,所以本实验将氮气不断向半敞开式加热炉e吹扫以实现样品加热及与空气隔绝。实验采用恒定接触面积模式的平板挤压模式,虽然有别于目前大部分平板挤压流动研究所采用的恒定体积式挤压,但可以精准地测出接触面积上作用力的大小。实验过程中,下圆板b固定不动,上圆板a以恒定速率或者恒定作用力向下运动,挤压板间的PC熔体,使得部分熔体被挤出,同时传感器d及时采集压力或位移信号,得到上圆板的挤压应力或者下移速率随时间的变化曲线。

图1 挤压流动测试设备示意图Fig.1 Schematic of squeezing flow testing apparatus
本实验选择Saibic公司生产的聚碳酸酯(OQ 2720)为研究对象,材料密度为1.2g/cm3,数均分子量为20264,熔体指数为8.9g/10min,玻璃化转变温度为149℃。实验之前将聚碳酸酯在120℃下真空干燥12h,以去除样品中的水分。实验研究平板初始间距、熔体温度和挤压速率三个因素对上圆板挤压应力的影响规律。
2 理论模型
目前存在大量黏性及黏弹性本构模型可以用来描述传统聚合物加工过程的流变学行为[11],也有学者针对稀溶液及低黏度熔体的挤压流动建立了相应的黏性及线性黏弹性本构模型[12],但它们均难以表征PC熔体在挤压过程中的流变规律。因此,本工作采用塑料加工广泛应用的PTT(Phan-Thien-Tanner)[11]模型及基于分子理论的 XPP(eXtended Pom-Pom)[13]模型来描述PC的非线性流变行为,并建立相应的流动理论模型。
PC熔体在圆板之间挤压流动沿圆心是对称的,熔体的惯性力和重力与黏性力相比很小,可以忽略不计,因此,熔体等温挤压流动过程中的控制方程在柱坐标系下简化为

式中:r,z分别表示径向和厚度方向;vr,vz代表相应方向的速度;σ,p分别代表Cauchy张量及压强;ηs,D分别表示熔体的黏度和剪切应变速率;τi为对应于第i个松弛时间谱的应力,若采用PTT模型,则

其中上随流导数定义为

式中:ηi,λi,ε分别表示第i个松弛时间谱的黏度、松弛时间及材料常数;τi为对应的应力。若采用XPP模型,则本构方程为

式中
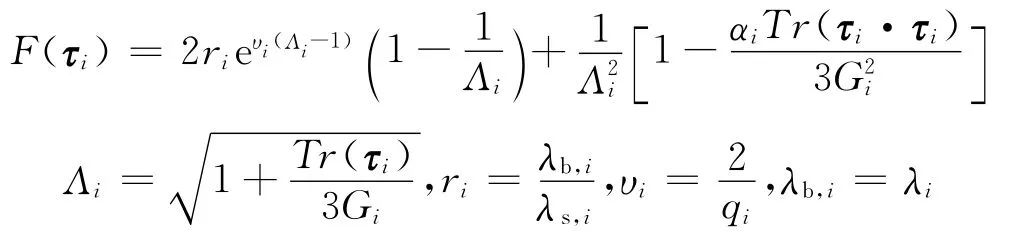
式中:αi为第i个松弛时间对应的非线性系数;Gi为第i个松弛时间对应的模量;λb,i为主链松弛时间;λs,i为受拉伸后的松弛时间;υi代表周围链拉伸后的影响参数;qi为主链上的支链数。
将本构方程(3)或(4)中的应力项代入动量方程得

采用有限差分离散连续性方程(1)、动量方程(5)~(6)及本构方程(3)或(4)得到关于压强p、速度v及应力τ的代数方程组,用松弛迭代法求解代数方程组即可得到离散点的物理量。然后,计算上平板上离散点垂直方向的合力
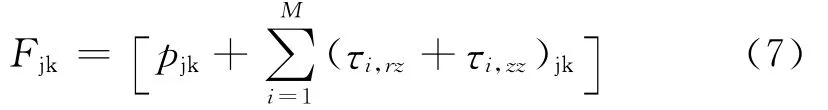
再用离散点上的Fjk作高斯插值计算上板的合力

式中N对应于流变仪采集的应力信号。
3 实验结果与分析
3.1 熔体温度对挤压应力的影响
图2为初始板间距1.0mm,挤压速率0.010mm/s,不同熔体温度下挤压应力随应变的变化情况。当温度达到573K时,挤压应力随应变变化缓慢,即使应变达到40%应力也仅仅只有1800Pa,应力-应变表现为两段式分布。当温度降至533K时,挤压应力随应变增长较快,应变为20%时应力已增至4350Pa,应力-应变呈三段式分布:挤压应力在应变初期(0%~2%)陡增,而后在2%~28%的较宽应变范围内基本呈现直线式缓慢上升,当应变大于28%,应力又表现出二次陡增现象。上述分布规律主要是PC熔体的黏弹特性所致,熔体的弹性随温度的降低而增大,温度越低,聚合物分子链对相同的应变表现出越大的回弹力,而挤压应力平稳增长区域(中等程度应变)为熔体对挤压应变的黏弹平衡区域。环境温度处于中间值553K时,PC熔体的弹性效应较弱,应力-应变的三段式分布并不明显。

图2 温度对熔体挤压应力的影响Fig.2 Influence of temperature on squeeze stress of the melt
3.2 挤压速率对挤压应力的影响
图3为上板在初始板间距1.0mm、熔体温度573K、不同挤压速率下挤压应力随应变的变化。对比图3与图2可以看出,针对应力-应变响应,提高挤压速率等效于降低熔体温度,说明熔体挤压过程存在类似的聚合物时温等效机制。在0.005mm/s和0.010mm/s的低挤压速率下,挤压应力表现出两段式分布:初始应力陡增对应应变在2%左右,而后应力随应变缓慢增加;当挤压速率增至0.020mm/s,挤压应力在应变25%时出现二次陡增现象。这是因为高温PC分子链的松弛显著,低速挤压,熔体分子受迫变形与松弛达到一定的局部平衡,表现出挤压应力的缓慢增加。挤压速率提高,分子链的松弛跟不上其挤压变形,弹性效应较显著,表现出挤压应力随应变的较快增长,也存在一个类似黏弹平衡区域。

图3 挤压速率对挤压应力的影响Fig.3 Influence of squeeze speed on the squeezing stress of the upper disc
3.3 初始板间距对挤压应力的影响
图4为环境温度573K,挤压速率0.010mm/s,不同初始平板间距对上板挤压应力的变化情况。实验选择相同的挤压行程0.43mm,可以看出,初始板间距越大,所需的挤压应力越小。初始间距选择2.0mm时,挤压应力在整个挤压过程中变化极缓慢,仅发生了228Pa的增长。当初始间距减小,上板所承受的挤压应力也随之增加,但并未出现低温和高挤压速率下的应力-应变三段式变化现象。平板初始间距越小,剪切速率越大,剪切应力和轴向应力相应增加,所以上板挤压应力随间距缩小呈现增大的趋势。
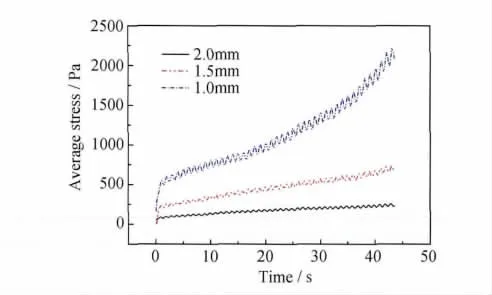
图4 初始板间距对挤压应力的影响Fig.4 Influence of initial squeeze separation on the squeeze stress
3.4 本构模型的适应性评价
Engmann[12]针对非牛顿黏性流体采用幂律模型建立了挤压流动模型,并导出了计算上板平均挤压应力的解析公式

式中:K和n为幂律流体参数;ε0为应变速率。
本工作分别采用幂律模型(见式(9))、PTT模型及XPP模型模拟挤压应力随应变的变化规律,并与实验数据对比以评价它们对PC熔体挤压流动分析的适应性。模型的参数(见表1)是通过旋转流变及挤压流变实验数据拟合而成。

表1 本构方程中的材料参数Table 1 Material parameters in constitutive equations
图5比较了挤压速率0.010mm/s,初始板间距1.0mm,熔体温度573K条件下幂律模型、PTT模型及XPP模型所描述平板挤压过程中上板挤压应力的变化情况。与实验结果对比发现,由于忽略材料的弹性效应,幂律模型无法描述聚碳酸酯熔体挤压过程的流变学行为,而PTT模型和XPP模型均能表征黏弹流体在挤压流动过程中应力随应变的分段式增加趋势,但PTT模型的预测值较实验测量值高,且在高应变下出现数值振荡。相比之下,基于分子论的XPP模型虽然在低应变区模拟值较高,但在之后较宽的应变范围内应力预测值与实验测量值吻合较好。
图6显示不同挤压速率下XPP模型在模拟PC熔体挤压流变的适应性。在低挤压速率下XPP的预测值与实验值较为接近;当挤压速率增大,XPP在25%以下的低应变区域内模拟值与实验值吻合较好,而应变进一步增大会引起明显的预测偏差,这主要是由于本工作所选PC的松弛时间谱数较少,特别是在长松弛时间区域,不能精确描述弹性效应所引起的二次应力陡增。


4 结论
(1)PC熔体挤压流动的黏弹性显著,温度越低,挤压速率越大,黏弹效应越明显。
(2)低温和高应变下PC熔体在挤压过程中应力会发生二次突增现象,表现出三段式分布,随着温度的降低和挤压速率增大二次突增愈加显著。
(3)黏性本构模型忽略了熔体的弹性,不能表征挤压应力的突增过程;黏弹性本构模型中XPP模型在低速及低应变情况下能较精确地描述PC熔体挤压流动过程的流变规律。
[1]WU C H,CHEN W S.Injection molding and injection compression molding of three-beam grating of DVD pickup lens[J].Sensors and Actuators A,2006,125(2):367-375.
[2]LEE S H,KIM S Y,YOUN J R,etal.Warpage of a large-sized orthogonal stiffened plate produced by injection molding and injection compression molding[J].Journal of Applied Polymer Science,2010,116(6):3460-3467.
[3]GUAN W S,HUANG H X,WANG B.Poiseuille/squeeze flowinduced crystallization in microinjection-compression molded isotactic polypropylene[J].Journal of Polymer Science:Part B:Polymer Physics,2013,51(5):358-367.
[4]PATHAM B,FOSS P H.Thermoplastic vibration welding:review of process phenomenology and processing-structure-property interrelationships[J].Polymer Engineering &Science,2011,51(1):1-22.
[5]LAUN H M,RADY M,HASSAGER O.Analytical solutions for squeeze flow with partial wall slip[J].Journal of Non-Newtonian Fluid Mechanics,1999,81(1-2):1-15.
[6]RAN X J,ZHU Q Y,LI Y.An explicit series solution of the squeezing flow between two infinite plates by means of the homotopy analysis method[J].Communications in Nonlinear Science and Numerical Simulations,2009,14(1):119-132.
[7]MEETEN G H.Yield stress of structured fluids measured by squeeze flow[J].Rheologica Acta,2000,39(4):399-408.
[8]CHAN T W,BAIRD D G.An evaluation of a squeeze flow rheometer for the rheological characterization of a filled polymer with ayield stress[J].Rheologica Acta,2002,41(3):245-256.
[9]DEBBAUT B. Non-isothermal and viscoelastic effects in the squeeze flow between infinite plates[J].Journal of Non-Newtonian Fluid Mechanics,2001,98(1):15-31.
[10]KARAPETSAS G,TSAMOPOULOS J.Transient squeeze flow of viscoplastic materials[J].Journal of Non-Newtonian Fluid Mechanics,2006,133(1):35-56.
[11]黄树新,江体乾.黏弹流体流动的数值模拟研究进展[J].力学进展,2001,31(2):276-288.HUANG S X,JIANG T Q.Development of numerical simulation for viscoelastic fluid flow[J].Advances in Mechanics,2001,31(2):276-288.
[12]ENGMANN J,SERVAIS C,BURBIDGE A S.Squeeze flow theory and applications to rheometry:a review[J].Journal of Non-Newtonian Fluid Mechanics,2005,132(1-3):1-27.
[13]VERBEETEN W M H,PETERS G W M,BAAIJENS F P T.Differential constitutive equations for polymer melts:the eX-tended Pom-Pom model[J].Journal of Rheology,2001,45(4):823-844.
