滚摆运动的研究
2013-12-01周艳丽王扬威陈英才
周艳丽,王扬威,王 超,陈英才
(台州学院 物理与材料工程系,浙江 台州318000)
1 引 言
物理学力学部分有比较多的守恒定律,如:动量守恒定律、机械能守恒定律、角动量守恒定律等.在实际教学中,为了增强学生对这些守恒定律的认识,往往需要引入实验对相关守恒定律进行演示和验证[1-3].在物理教学中,滚摆实验常被用来演示机械能守恒定律.
实际上,滚摆在运动过程中机械能是不守恒的.一方面,运动过程中总有空气阻力、摆线间摩擦力等非保守力做功;另一方面,如果摆线没有弹性或摆线弹性可忽略,那么滚摆每次运动到最低点时都会因为摆线间摩擦及摆线内摩擦而损失掉所有的平动动能[4].针对滚摆运动问题,目前已有不少的研究[4-10],但这些研究往往只侧重于分析和讨论理想条件下(即忽略空气阻力、摆线间摩擦力等因素的影响)滚摆在1次全滚动过程中的运动特点和能量损失,而对于滚摆在多次全滚动中所遵从的运动规律以及阻力、摩擦力等因素造成的机械能损失却少有讨论.这明显不利于学生对滚摆运动规律的完整认识和把握.本工作的主要目的就是从实验上研究滚摆滚动最大高度和滚动时间随滚动次数的变化规律,并在理想条件下从理论上讨论分析实验结果.同时,通过对比实验和理论结果,揭示了空气阻力、绳间摩擦力等因素对滚摆运动的影响及其所造成的系统的机械能损失.
2 实 验
滚摆的核心部件为由金属轴和金属轮组合而成的复合刚体,复合刚体由轴两端的摆线对称的悬挂在演示支架上,如图1所示.把摆线均匀地绕在轴的两端,使滚摆提升至一定高度,然后平稳释放,滚摆将在重力和摆线拉力作用下重复向下和向上滚动.如果忽略能量损失,那么滚摆每次上滚的最大高度都相同,这说明滚摆在运动过程中机械能守恒,重力势能和动能循环相互转换.
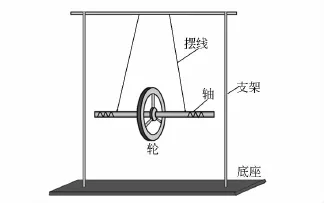
图1 滚摆实验装置示意图
实验所用的滚摆装置主要参量:轴和轮的半径分别为2.06mm和47.27mm;轴和轮组成的复合刚体总质量为234.47g;复合刚体对轴的转动惯量为3.199×10-4kg·m2(由三线摆实验仪多次测量平均得到);摆线为三股加捻锦纶线(捻度约为300捻/m,直径约为0.7mm).转轴侧面上靠近轴两端处对称地分布着2个小孔(直径约为1mm).轴的两端均为空心(空心部分直径约为2mm),且各自与对应端轴侧面上的小孔连通.在安装摆线时,首先取2根长度相等的摆线,并分别在一端打结;然后,将未打结的一端穿入轴端空心部分并由侧面上小孔穿出.拉紧摆线,使摆线的绳结阻挡在轴端的空心部分,从而完成摆线与轴的固定;最后,分别将2根摆线未打结端绑定在悬梁对应侧的吊钩上.悬梁上的2个吊钩,一个位置固定,另一个高度可微调.摆线连接完成后,微调吊钩高度以保证2条摆线的长度相等.另外,为了量化运动过程中滚摆的高度(位置)变化,将最小分度为1mm的米尺竖直固定在支架一侧的立柱上,并用滚摆轴上边缘(或下边缘)的延长线在米尺上对应刻度值的改变来表征滚摆的高度变化.
实验时,首先记录滚摆静止(即滚摆在最低点)时轴在米尺上对应的刻度值,并将之定义为高度零点;随后把摆线均匀地绕在轴的两端,使滚摆提升至初始高度H0并平稳释放.滚摆的整个运动过程及时间由固定于实验装置正前方的高清晰摄像机记录.实验所选用的滚摆初始高度H0分别为:31.17,27.17,23.17,19.17,15.17cm.对于每一初始高度分别做5次实验,每次实验记录30次以上的全滚动.根据摄像机录像读取滚摆第n次全滚动后滚摆的最大高度H(n)以及经历n次全滚动所需要的总时间T(n),并对数据做平均处理.考虑到不同初始高度所得到的数据变化规律相似,这里只给出初始高度为31.17cm时H(n)以及T(n)随滚动次数n的变化,如图2和图3所示.图中的虚线为理想条件下的理论结果,实线为用理论上得到的函数关系对实验数据的拟合曲线.系统机械能在滚摆运动过程中不断损失,从而使得滚摆滚动最大高度随滚动次数的增多不断减小,如图2所示.另一方面,滚动次数越多,运动经历的时间就越长,从而使得滚摆滚动时间随滚动次数的增多不断增大,如图3所示.
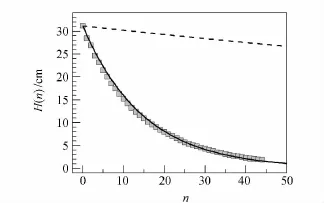
图2 滚摆最大高度Hn随摆动次数n的变化

图3 滚动时间T(n)随摆动次数n的变化
3 理论分析
理想条件下忽略空气阻力和绳子摩擦力等因素影响,只考虑滚摆在最低点的平动动能损失,理论上可以证明[5]以下几个问题.
1)在下滚和上滚过程中,滚摆质心作匀变速直线运动,加速度a0可表示为

其中,M为轮和轴的总质量,r为轴的半径,I为轮和轴构成的复合刚体对轴的转动惯量.
2)在1次全滚动中(由初始最高点下滚,经过最低点,然后再上滚至新的最高点)滚摆上滚最大高度H(n+1)与下滚初始高度H(n)之间存在简单的正比关系
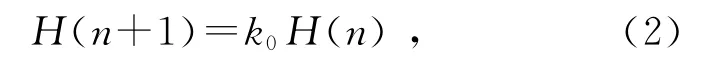
其中系数k0为

由式(2)可以递推得到n次全滚动后滚摆所能达到的最大高度H(n),即滚摆滚动最大高度随滚动次数的变化关系

这里H0代表滚摆的初始高度.
单就1次全滚动而言,滚摆质心的运动可以分为3个部份:
1)下滚阶段,质心由最高点匀加速直线运动到最低点;
2)反转时刻,滚摆在最低点与摆线发生瞬间相互作用,质心速度方向发生反转;
3)上滚阶段,质心由最低点匀减速直线运动到新的最高点.结合式(1)和(4)可求出滚摆第n次全滚动中所需要的时间

由式(5)可以得到滚摆经过n次全滚动所用的总时间T(n),即滚摆滚动时间随滚动次数的变化关系

其中常数B0表示为
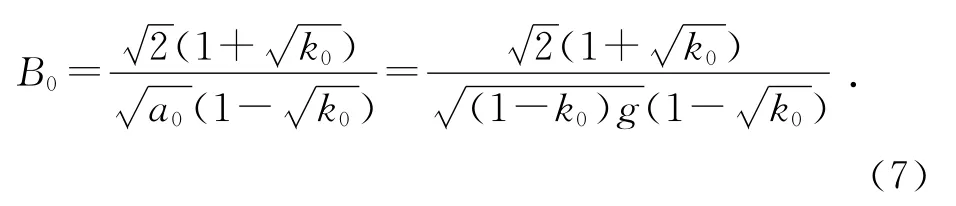
取重力加速度g=9.8m/s2,并将轴半径r、轮和轴的复合体总质量M及其对轴的转动惯量I值代入式(3)和(7)可以得到k0=0.996 9,B0≈1 045s/cm1/2.k0非常接近于1,这表明在理想条件下,实验所用滚摆在最低点处的平动动能损失很小,从而可以比较好地演示机械能守恒.图2和3中的虚线分别给出了理想条件下滚摆最大高度和滚动时间随滚动次数的变化曲线.可以看出,理论结果与实验数据有很大差别.这是因为上述理论推导忽略了空气阻力、摆线间摩擦力和摆线的内摩擦等因素的影响.很明显,上述因素对滚摆运动有重要影响:空气阻力、绳子间摩擦力等非保守力做功消耗机械能,使滚摆最大高度随滚动次数的衰减得更快,如图2所示;同时,阻力、摩擦力等的存在使下滚过程中的加速度减小,而使上滚过程中的加速度增大.当阻力、摩擦力等比较小时,滚动时间随滚动次数的增大要比理想情形的缓慢,如图3所示.
尽管实验数据在量值上与理论结果不同,但是实验结果可以用理论上给出的函数关系[式(4)和(6)]描述,如图2和图3中的实线所示,滚摆最大高度随滚动次数的变化关系可表示为:
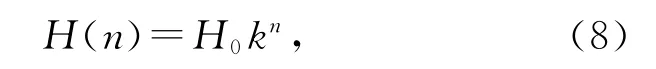
滚摆滚动时间随滚动次数的变化关系可表示为
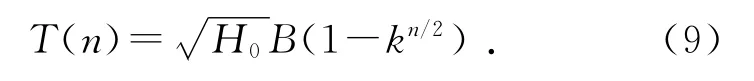
对于不同的初始高度,表1给出了拟合得到的系数k和B.可以看出,k和B与理论值k0和B0有很大的差别.另外,随着初始高度的增大,k和B值都有减小的趋势,这意味着:初始高度越高,滚摆系统机械能损失得就越快.但是,从数值上看,初始高度对k和B值的影响还是比较微小,因此可以粗略地认为k和B只与系统自身属性有关.为了进一步说明实验结果和理论结果在量值上的差别,用拟合得到的k替代k0,并由式(7)计算得到了B′,如表1所示.可以看出,B值与B′值也有很大的差别.这是因为:在实际条件下,由于阻力、摩擦力等的存在,滚摆下滚和上滚过程中的加速度不再相等,而下滚和上滚过程中加速度相等恰恰是式(7)成立的条件.
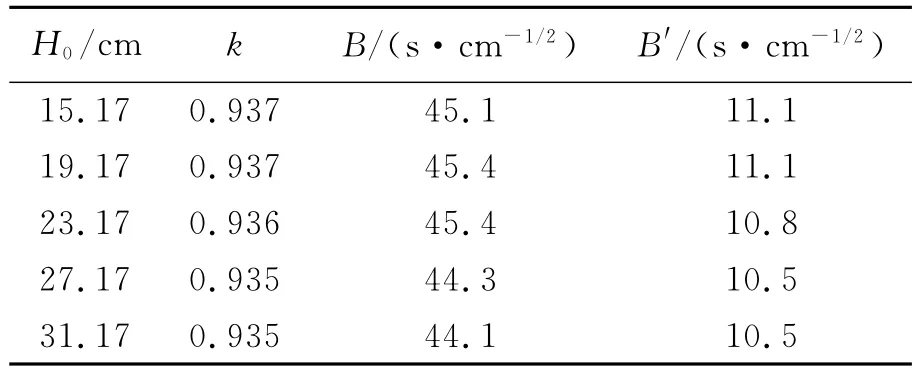
表1 不同初始高度对应的系数k和B
滚摆运动过程中空气阻力、绳子间摩擦力等是不可忽略的因素,其做功也是系统机械能损失的重要来源.假定用Wf(n)表示第n次全滚动中上述阻力和摩擦力因素消耗的机械能总量,那么由k0和k则得到Wf(n)随滚动次数的变化关系:
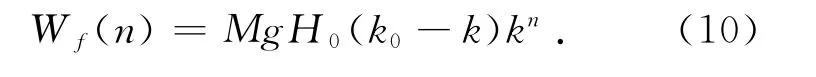
4 结束语
从实验上研究了滚摆运动过程中滚动最大高度H(n)和滚动时间T(n)随滚动次数n的变化,并从理论上推导出了理想条件下H(n)及T(n)关于n的函数关系.研究结果表明:由于空气阻力和摆线间摩擦力等因素的存在,实验结果在量值上与理想条件下的理论结果并不一致,但是,实验结果仍可由理论得到的函数关系描述;对比实验和理论结果可以确定空气阻力、摆线间摩擦力等因素所造成的系统机械能损失.
[1]白云.用3dsMax8模拟碰撞中的动量守恒实验[J].物理实验,2007,27(5):39-41.
[2]樊利芳.验证机械能守恒定律实验的改进[J].物理实验,2011,31(9):19-20.
[3]王佑坤.自制角动量守恒演示仪[J].物理实验,2011,31(10):33-35.
[4]李洪政.麦克斯韦摆运动的剖析[J].徐州师范学院报,1990,8(3):64-66.
[5]韦德全.麦克斯韦滚摆的能量损失[J].济宁师专学报,1997,18(3):29.
[6]应干华.麦克斯韦摆运动过程中的超重和失重现象研究[J].物理教学探讨,2004,22(3):41-42.
[7]王阳,袁晓忠.滚摆演示实验内容的扩充[J].物理实验,1999,19(5):46.
[8]杨静生.滚摆运动的动力学分析[J].技术物理教学,2007,15(1):36-37.
[9]何汝鑫.滚摆运动过程中能量转换的分析[J].物理,1963,(2):90-91.
[10]卢克箴.马克士威尔滚摆运动的研究[J].陕西师大学报(自然科学版),1985,(3):89-94.
