应用PCA-SVM对伺服阀进行故障诊断

王 磊 屈卫东

(上海交通大学电子信息与电气工程学院，上海 200240)

0 引言

电液伺服阀是将电量转变成液压输出量的电液转换元件，是电液伺服系统的核心部件。电液伺服阀具有动态响应快、控制精度高和使用寿命长等优点，被广泛应用于航空、航天、舰船、冶金和化工等领域。但由于电液伺服阀内部结构复杂、精密度高、价格昂贵且工作环境恶劣(高温高压)，其发生故障的频率较高。电液伺服阀性能的好坏将直接影响整个液压系统的稳定性和控制精度，因此，对电液伺服阀进行故障诊断具有重要的工程意义。

针对某型电液伺服阀，通过调整模型参数模拟故障发生并提取故障数据。故障数据的分类采用支持向量机算法。考虑到原始故障数据的初始维数比较高，为了提高支持向量机的训练速度和分类速度，采用数据压缩算法(主元分析法和小波包频域分析)进行数据的预处理。

故障分类算法的实现形式包括支持向量机(support vector machine，SVM)、主元分析法-支持向量机(principal component analysis-support vector machine，PCA-SVM)和小波包能量特征向量-支持向量机(wavelet packet energy eigenvector-support vector machine，WPEE-SVM)。

1 电液伺服阀建模

1.1 电液伺服阀工作原理

双喷嘴挡板型电液伺服阀工作原理为［1］:由力矩马达的通电线圈产生电磁偏转力矩，使衔铁挡板组件发生偏转;挡板的偏转将引起喷嘴节流口变化，进而导致液流背压变化并作用到阀芯，引起阀芯移动;阀芯推动反馈杆，反作用于衔铁挡板，直至反馈力矩和电磁力矩平衡，阀芯停留在某一位置。因此，主阀芯的位移量能精确地随着电流的大小和方向而变化，从而控制通向液压执行元件的流量和压力。

1.2 电液伺服阀的液压仿真模型

AMESim的全称为系统工程高级建模和仿真平台，是法国IMAGINE公司推出的基于键合图的液压和机械系统仿真及动力学的仿真软件。AMESim是传动系统和液压机械系统建模、仿真及动力学分析软件，它为用户提供了一个系统工程设计的完整平台，可以建立复杂的多学科领域系统的数学模型。

喷嘴挡板可以调用AMESim零件库中现成的模块。伺服阀的喷嘴模型可采用AMESim元件库中的弹簧阻尼元件和位移-流量模块构成。电液伺服阀的阀体与阀芯采用AMESim元件库中的流量-位移模块、压力-位移模块、质量模块和腔体元件组合［2］。

1.3 电液伺服阀的故障模拟

本仿真试验通过调整液压模型的参数，模拟仿真了电液伺服阀的6种状态，即正常状态、左端限位、右端限位、左侧喷嘴阻塞、右侧喷嘴阻塞和力矩马达磁性减弱，具体示意图如图1所示。

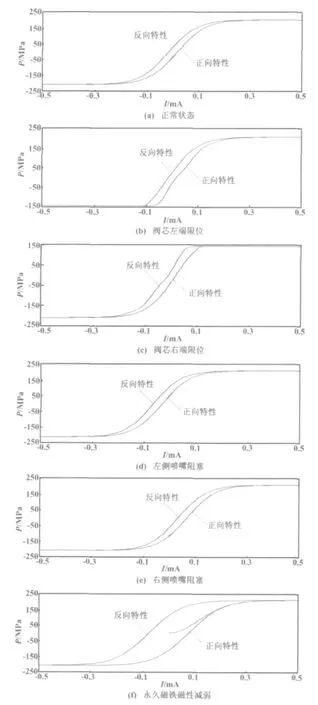
图1 电液伺服阀的6种状态Fig.1 Six states of the electro-hydraulic servo valve

电液伺服阀特性曲线包含正向特性曲线和反向特性曲线，两者并不完全重合，特性曲线具有一定的滞环。

在正常状态下，电液伺服阀的压力特性曲线是与输入电流呈回环状的函数曲线。当电液伺服阀处于阀芯一端限位状态时，阀芯运动到限位位置而无法继续运动，此时压力维持在某个恒定值。

在喷嘴阻塞状态下，阀芯的运动特性并不受影响，特性曲线的形状和正常状态下的曲线基本一致，只是其特定曲线与正常状态下的曲线有一个偏移量，其表现就是特性曲线整体左移或者右移。

力矩马达磁性的减弱，主要是因为磁铁使用时间太久等原因。这种情况会导致整个的电液伺服阀的反应速度降低，使压力特性曲线滞环变大、斜率减小［3］。

对于电液伺服阀的6种状态，分别选取15 MPa、18 MPa、21 MPa、24 MPa和27 MPa作为油压进行仿真，同时通过设置不同的故障参数模拟多种故障程度，获取具有代表性的特性曲线。

对仿真得到的压力特性曲线进行离散采样，获取特征故障数据［4］。其中，在正向特性曲线和反向特性曲线各取19个点，即对每个特性曲线采样38个点作为相应状态的特征数据。显然，特征数据为38维，这些特征数据将通过SVM、PCA-SVM和WPEE-SVM这3种分类算法实现分类处理。

2 数据分类处理

2.1 数据压缩降维

由于原始故障数据维数较高，大大影响了SVM的分类速度，因此，首先对数据进行降维预处理，并在此基础上采用SVM对数据进行分类。PCA、WPEE主要对特征数据进行降维处理，以提高向量机的训练速度和分类速度。其中，PCA是常用的线性数据降维算法;WPEE用来提取故障数据的频域特征信息，从而实现数据压缩。

2.1.1 主元分析法

PCA是一种线性的数据挖掘算法，用于提取数据主元，以去除噪声和冗余，实现数据降维［5］。

假设有一组具有m个观测变量、n个采样时间点的采样数据矩阵X1。对X1进行中心归零化得到X［6］，X的协方差矩阵为CX=XXT。寻找一正交阵P，使Y=PX，且 CY=YYT为对角阵。CY=P(XXT)PTPVΛVTPT(Λ 为对角阵 λ1，λ2，…，λn，V 为正交阵)，所以取 P=VT，则可得 CY=Λ。其中，矩阵CY对角线上第i个元素是X在Pi方向上投影后投影系数的方差。对角线上的元素越大，表明信号越强;反之，则表明可能是存在的噪声或次要变量。

定义累计误差贡献率，当 sum足够大时，选取P的前K行作为投影矩阵P'，通过P'X可将原有数据降为K维。

2.1.2 小波包分析法

小波包分析能够为信号提供一种更加精细的分析方法。与小波分析相比，小波包分析不但能够对信号的低频部分进行分解，而且也能够对信号的高频部分进行进一步的分解。同时，它也能够根据被分析信号的特征，自适应地选择相应频带，使之与信号频谱相匹配，从而提高了时间-频率分辨率［7］。

3层小波包分解原理如图2所示。

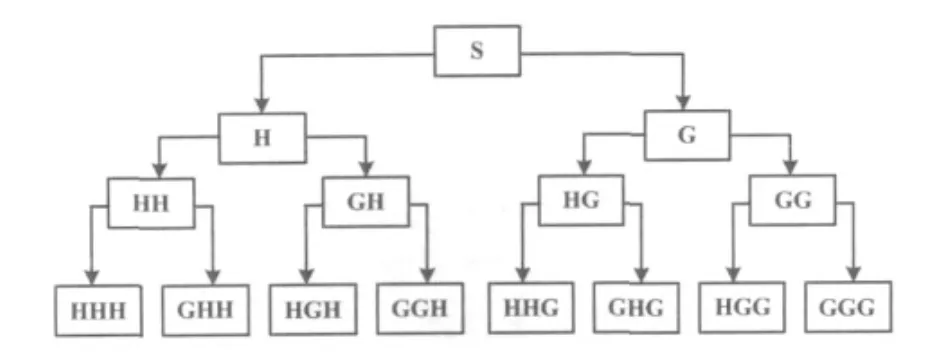
图2 小波包分解原理图Fig.2 Principle sketch map of wavelet packet decomposition

图2中，S代表原信号、H代表低频、G代表高频。对于任意给定的信号S，通过一组高低通组合的共轭正交滤波器组G、H，不断地将信号划分到不同的频段上。分解关系如下:S=HHH+GHH+HGH+GGH+HHG+GHG+HGG+GGG。

对信号进行小波包分解的层数视具体信号和对特征参数的要求决定，使用时可采用小波包分解信号的范数表示所在频带的信号能量大小。一般来说，在正常运行状态与故障状态下，输出信号的各频带成分是不同的，因此可以根据信号能量的大小建立特征向量，用于区分系统不同的状态［8］。

2.2 支持向量机

故障数据分类是重要的数据挖掘技术，分类的目的就是根据数据集的特点构造一个分类器。分类算法包括决策树、KNN法、VSM法、贝叶斯法、神经网络和SVM法［9］。这些算法各有优劣。其中，KNN算法较适用于样本容量较大的类域的自动分类，对于小样本容易误分。VSM算法更适用于文档分类。贝叶斯方法建立在类别总体概率分布和各类样本概率密度分布函数的基础上，难以应用于实际情况。在实际应用中，通常采用神经网络和SVM法。神经网络是基于经验风险最小化原则的学习算法，存在一些固有的缺陷，如神经网络结构的选择往往依据经验。SVM算法建立在统计学基础上，其分类的效果不受样本数量的限制，特别适用于小样本的故障分类。电液伺服阀故障样本比较少，因而采用SVM作为故障分类算法［10］。

SVM算法建立在统计学原理基础上，我们可以简单地将SVM算法理解为对于最优分离超平面的求解。设给定训练集{(x1，y1)，(x2，y2)，…，(xi，yi)}，其中 xi∈Rn，yi∈{1，-1}，最优分离超平面方程为(wx+b)=0，b 为偏移量。xi代表样本数据，yi代表样本数据的分类(如果xi属于第一类，yi=1;如果xi属于第二类，则yi=-1)。

设对所有样本xi满足以下不等式:

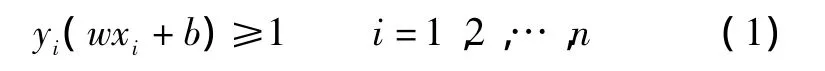
则正反数据间隔d为:

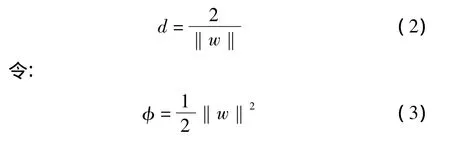
定义如下的Lagrange函数:

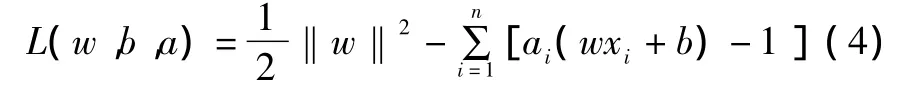
式中:a≥0，为Lagrange乘子。根据已知条件，易证明原问题与其对偶问题是强对偶关系。因而可将上述最优分类面的求解问题转化为对偶问题。

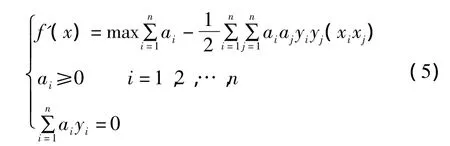
式(5)是一个二次函数的寻优问题，存在唯一解。求解后即可得到分类面函数为:

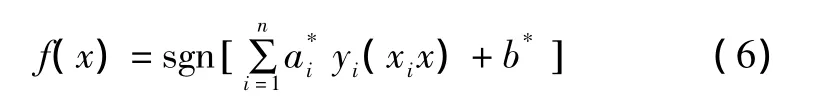
将样本数据代入式(6)，就可以判定对应样本所属的分类。如果原始问题是非线性的，即可通过将原有数据映射到高维空间，进而将原问题转化为高维空间中的线性问题。映射函数自身很复杂，但Mercer定理证明了内积核函数的存在性。这样SVM通过核函数K巧妙地实现了高维映射［11］。变换后目标函数和分类函数如下:

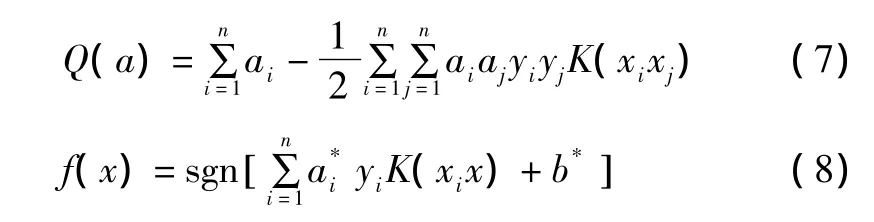
常见的核函数有线性核函数、多项式核函数、RBF核函数和Sigmoid核函数。

3 仿真算法实现

针对前面模型仿真提取的38维特征故障数据，分别采用SVM、PCA-SVM、WPEE-SVM这3种算法进行故障分类，并比较分类结果。

3.1 PCA 数据降维

运用主元分析法对故障样本数据进行数据降维分析，得到的主元贡献率如图3所示。

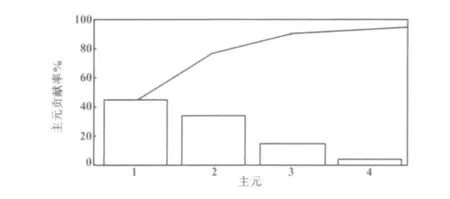
图3 主元贡献率Fig.3 Contribution rate of principal component

从图3可以看出，当取前4个主元时，其贡献率就可以达到96%以上，完全可以用来表述原有的故障数据。因此，选用前4个主元变量，将原有38维的数据降到4维。

3.2 小波包数据处理

压力特性曲线具有滞环，为实现对曲线数据的频域分析，在频域分析前对原特性曲线进行处理，以去除滞环，形成单条连续波形曲线。其处理方式为:正向特性曲线维持不变，反向特性曲线以电流Ⅰ=0.5 mA为轴作镜像对称，可得到原始信号和小波包重构信号的比较曲线。

相关仿真表明，正常状态和喷嘴阻塞这两种状态下各频段的能量波形分布和能量的幅值存在着明显差异。因此，可以利用小波包分解提取不同故障状态下的能量特征向量，以进行故障分类。

小波包能量特征向量的提取实现过程具体如下。

①将信号小波包分解，采用wpdec(Matlab一维小波包的分解函数)。WPEE=wpdec(s1，3，’db1v’，’shannon’);使用db1小波基对x进行3层分解，采用默认的熵标准。

②采用wprcoef函数对分解系数进行重构，提取各频带范围的信号特征。

③采用norm函数求取各频段信号的总能量(即重构信号离散点幅值矩阵的范数)。

④构造特征向量。将各个频段能量结合起来组成8维小波能量特征向量，最终将原有数据由38维降至8维。

3.3 算法比较

SVM算法采用LibSVM软件包，具体实现采用C-SVM。惩罚因子C起到控制学习误差的作用，C越小，学习误差越大，训练时间越长，但训练得到的SVM具有较强的推广能力;C越大，学习误差越小，分类迅速，但训练得到的SVM推广能力就弱。多次试验表明，核函数选取最常用的RBF核函数，C的值选为1。

基于上述参数配置，分别采用SVM、PCA-SVM和WPT-SVM算法对前面模型仿真中提取的38维故障数据进行分类。故障分类结果对照表如表1所示。

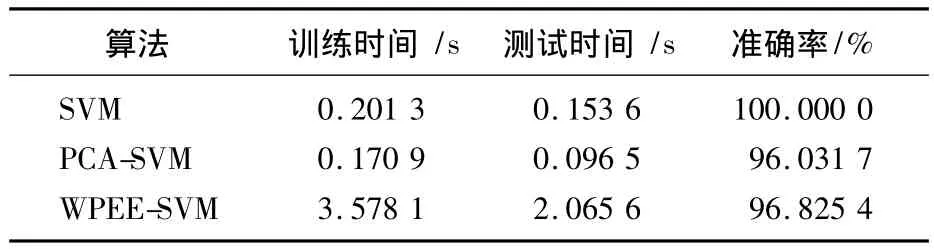
表1 算法结果比较Tab.1 Comparison of the results

从表1可以看出，尽管WPEE-SVM算法可以对原始数据提取频域特征进行数据的压缩降维，但由于需要对其进行小波分解等复杂操作，反而大大降低了分类速度和测试速度。经PCA-SVM压缩后，特征数据的训练时间和测试时间均有所减少。在对精度要求不高的情况下，显然应该选择PCA-SVM算法。

4 结束语

本文讨论了某型电液伺服阀故障诊断的算法实现，验证了算法的可行性。首先利用机理建模建立了对应电液伺服阀的液压仿真模型，再通过修改模型的参数，完成了故障植入并提取了故障特征信息。随后分别采用PCA、PCA-SVM和WPEE-PCA算法对故障进行了分类，并验证了这3种算法的有效性。与SVM相比，PCASVM算法在速度上得到了提高，准确率略有下降;但在大样本实时系统中，该方法具有较大的优势。

［1］施康，曾良才.基于AMESim仿真的电液伺服系统故障诊断的研究［D］.武汉:武汉科技大学，2009.

［2］张东，叶志峰.发动机主燃油控制系统建模仿真和试验验证［D］.南京:南京航空航天大学，2008.

［3］李成，曾良才.基于B-P神经网络的电液伺服阀的故障诊断［D］.武汉:武汉科技大学，2010.

［4］曾良才，孙国正.基于特性曲线的电液伺服阀神经网络的故障模式识别［J］.中国机械工程，2002，10(3):835-838.

［5］肖江，蒋爱凭.基于PCA的SVM故障诊断方法的研究与应用［C］//第十届全国信息技术化工应用年会论文集，北京:中国化工学会信息技术应用专业委员会，2005:83-86.

［6］Jolliff I T.Principal component analysis［M］.New York:Springer-Velag，1986.

［7］Zhang J Q，Yan Y.A self-validating differential-pressure flow sensor［C］//IEEE Instrumentation and Measurement Technology Conference，Chatham，Kent ME44TB UK，2001:1227-1230.

［8］Daubechies I.Orthonormal bases of compactly supported wavelets［J］.Communication on Pure and Applied Math，1988，41(7):909-996.

［9］Vapnik V N.统计学习理论的本质［M］.张学工，译.西安:西安电子科技大学出版社，2008:43-57.

［10］Kotsiantis S B.Supervised machine learning:a review of classification techniques［J］.Informatica，2007(31):249-268.

［11］Cristianini N，Shawe-Taylor J.An introduction to support vector machines and other kernel-based learning methods［M］.Beijing:Publishing House of Electronics Industry，2004:15-23.