基于模糊层次分析与证据推理的计算机平台评估

付建民，刘 因，宋蓓蓓

(1.安徽工业经济职业技术学院 计算机科学技术系，安徽 合肥 230051； 2.合肥工业大学 资源与环境工程学院，安徽 合肥 230009)

基于模糊层次分析与证据推理的计算机平台评估

付建民1，刘 因2，宋蓓蓓1

(1.安徽工业经济职业技术学院 计算机科学技术系，安徽 合肥 230051； 2.合肥工业大学 资源与环境工程学院，安徽 合肥 230009)

计算机平台的选择直接影响高等院校的职业化教育发展.将证据推理方法中指标的权重推广到三角模糊数，从定量与定性相结合的角度建立了一个多属性评价模型，证明了云平台优于传统平台和虚拟化平台.首先介绍了传统平台、虚拟化平台和云平台的概念；其次考虑决策过程的模糊性和不确定性，建立了基于FAHP和ER的计算机平台评估模型；最后应用该模型对上述三种平台的综合绩效进行了评估，验证了该模型和云平台的有效性、先进性.

云平台；多属性决策；模糊层次分析法；证据推理

0 引言

随着国家信息化步伐的加快和高等院校规模的扩大，培养具有实践能力的专业人才已成为高等教育的主要目标之一.高校的计算机平台在对计算机及相关专业学生的实践能力培养、考核和提高过程中起到了重要作用.如何建设高校的计算机平台已经成为重要课题，其核心为平台架构技术.平台架构技术包含了三个相继出现又共同并存的阶段，即传统平台、虚拟化平台和云平台.

基于传统平台的高校计算机实训室耗资大，占地广，用途单一，资源浪费严重.而基于寄居架构技术的虚拟化平台存在诸多技术瓶颈.因此，近年来以裸金属架构技术和云计算技术为核心的云平台代表了计算机平台架构的发展方向.诸多文献在该领域做了大量应用研究，[1-4]但目前，将云平台架构技术应用于计算机平台建设的高等院校还很少.因此，在各高校中大力推广和普及该方法的应用，是否具有可行性和必要性，是本文研究的目标之一.

证据推理(Evidence Reasoning，ER)方法是处理(Multiple Attribute Decision Making, MADM)多属性决策问题的一种有效方法，它对于解决具有主观不确定性、定量和定性指标共存的多属性决策问题具有良好效果.[5]近年来，ER方法在多属性决策领域应用越来越广泛.但是，已有的ER方法中，评价指标的权重无论是精确值或区间值都是直接给出的，其来源和得出方法没有介绍.本文将证据推理方法中指标的权重推广到了三角模糊数，使得其能够解决更为一般的群体决策问题.层次分析法(Analytic Hierarchy Process, AHP)是确定指标权重的一种基本方法，考虑专家判断的不确定性，本文将模糊层次分析法(Fuzzy Analytic Hierarchy Process，FAHP)引入到证据推理方法指标权重值的确定过程中.分别对传统平台、虚拟化平台和云平台的综合效用值进行评估和比较，以验证云平台是否能替代传统平台和虚拟化平台应用于高校的计算机平台搭建，为下一步的推广和普及提供理论依据.下面首先介绍传统、虚拟和云平台的概念，然后建立了基于FAHP和ER的计算机平台评估模型并对上述三种平台的综合绩效进行了评估，最后根据评估的结果给下一步的实际工作提出了合理化建议.

1 计算机平台架构

1.1传统平台

传统平台(图1)是物理的、静态的，存在着严重的资源浪费的问题.高校中的不同专业，课程和项目均需使用计算机通用或专业机房，一个普通高校往往架构了几十至上百个机房，而每个专业机房的利用率则很低.

图1 传统平台

1.2虚拟化平台

本世纪初，虚拟化技术与虚拟机的出现展开了计算机平台的动态架构理念，以寄居架构技术为基础的虚拟化平台(图2)开始应用于一些高校中，相对传统平台，该平台具有逻辑性、动态性的特点.

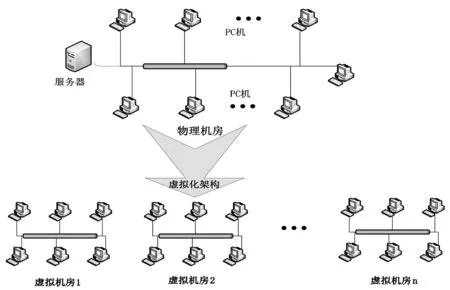
图2 虚拟化平台

虚拟化平台具有应用广泛、功能强大、管理方便等一系列优点.但是，虚拟化平台也存在技术瓶颈——寄居架构技术.基于寄居架构的虚拟化层运行于主机操作系统之上，依靠主机操作系统模拟硬件设备，虚拟机不能直接访问物理机的硬件，从而使应用能力与应用范围受到一定的影响.

1.3云平台

云计算是计算机发展史上的又一种革命.传统平台和虚拟化平台已经难以支撑云计算方法的应用与实施.为了更好地应用云计算技术及相关服务，基于裸金属架构技术和云计算技术的云平台(图3)被搭建并应用于各领域.

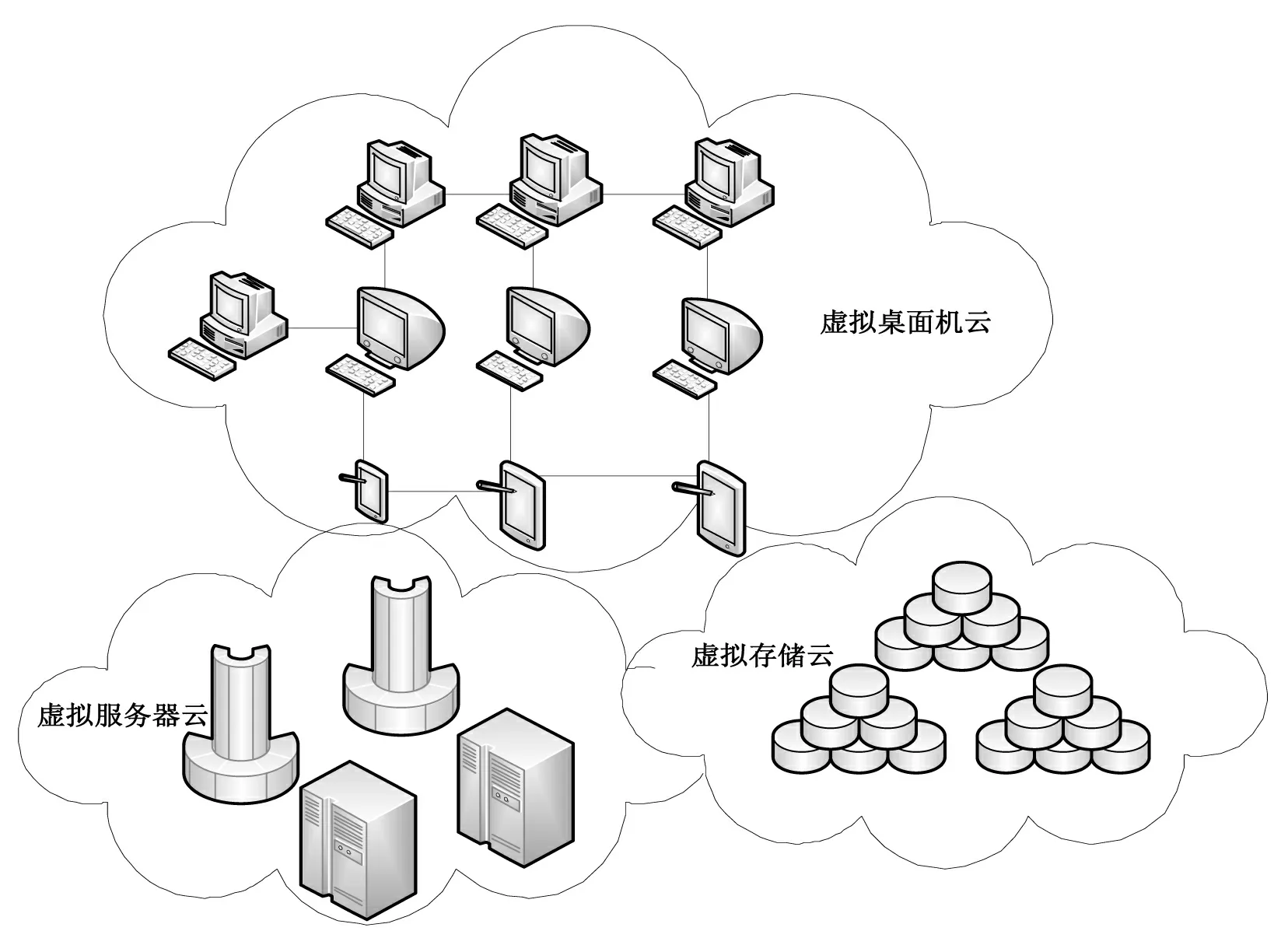
图3 云平台

虚拟化如果从结构上分，可以分为(bare metal)和寄居架构，[6]裸金属架构虚拟化是在计算机硬件上直接进行虚拟化.通过裸金属架构的虚拟化，虚拟机的底层是虚拟出来的CPU、内存等计算机硬件资源，而不是操作系统，虚拟机之间完全的独立.随着云计算技术的发展和大量应用，[7-8]基于裸金属架构技术和云计算技术的云平台已经成为近年来平台技术发展的趋势.[9]

平台的建设或改造需要投入大量人力、物力、财力.云平台的建设能否在高校中普及，需要充分的理论支持.本文将该问题作为一个典型的(Multiple Attribute Decision Making, MADM)多属性决策问题进行了深入分析和研究，考虑到该决策过程的模糊性和不确定性，本文提出了一个基于FAHP和ER的新的决策模型.分别对传统平台，虚拟化平台和云平台的综合效用进行评估，为云平台技术在各高校计算机平台建设中的应用和推广提供理论支持.下文首先结合计算机平台构建指标体系，然后建立基于FAHP和ER算法与模型，最后使用该模型对三种平台的综合效用值进行评估.

2 基于FAHP和ER的计算机平台评估模型

2.1构建指标体系

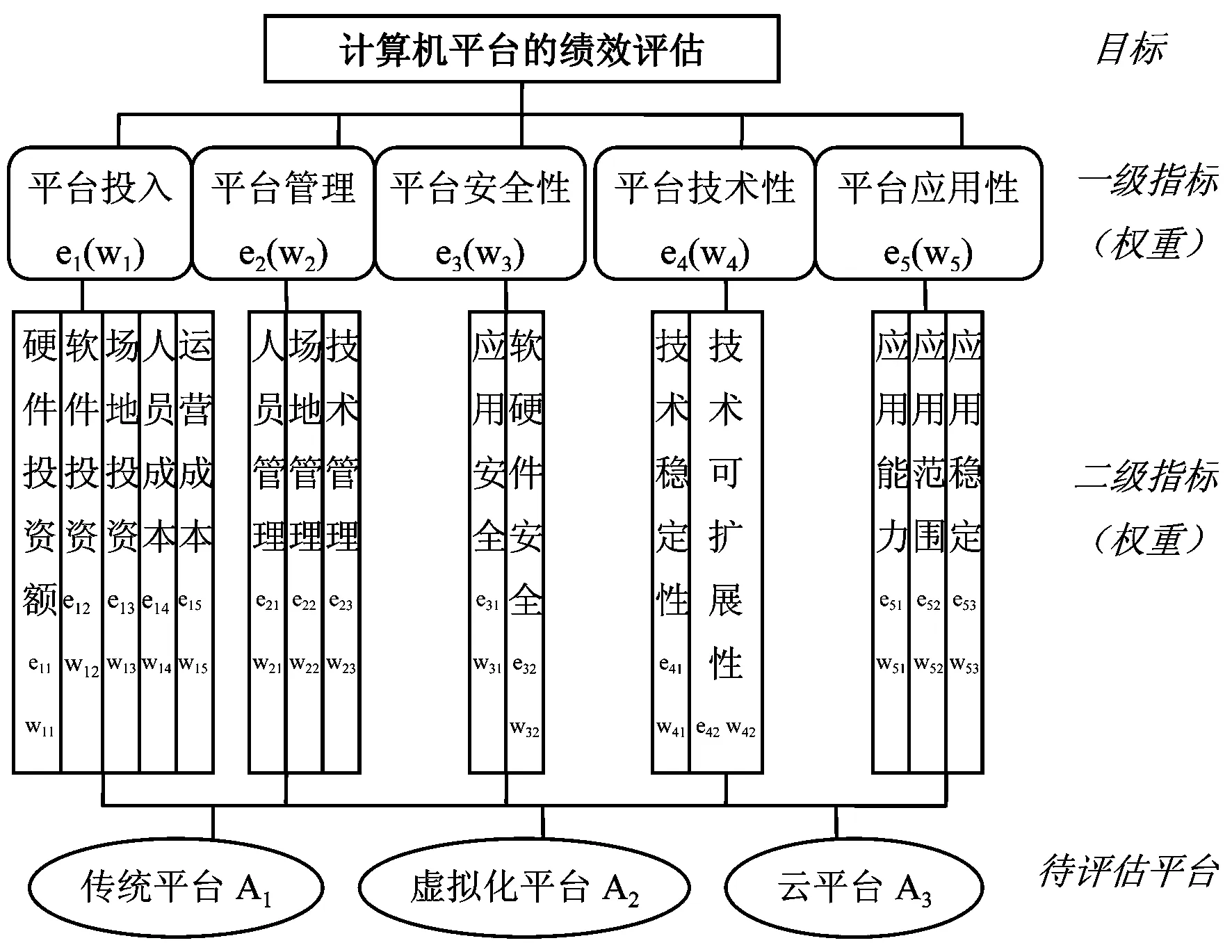
图4 计算机平台的绩效评估指标体系

决策问题中，指标体系常由三类基本层次组成：目标层、指标层、方案层.评价指标设计时应遵守系统性、动态性、相对独立性、可比性和可测性、灵活性、定性分析与定量分析相结合等原则.[10]本文借鉴PDCA的思想，采用问卷统计和专家分组讨论相结合的方法建立了基于ER的计算机平台评估指标体系，如图4所示.

2.2基于模糊层次分析法(FAHP)确定指标权重

AHP方法是一种确定指标权重的基本方法.但是，传统的AHP方法采用确定的数字表示决策者的主观判断，忽视了判断过程中的模糊性.因此，Buckley将模糊理论与AHP结合起来，[11]提出了模糊层次分析法(Fuzzy AHP)，FAHP在构造两两比较判断矩阵时，用模糊数代替确定值来表示诸如专家判断等模糊信息，将两两比较值模糊化并得到模糊权重，最后通过非模糊化将模糊判断的不确定性在形式上转化为确定性.

2.2.1 三角模糊数的表达

定义1 设X={x1,x2,…,xn}为一个论域，则定义在此论域上的模糊集M可以表示为：

M=μM(x1)/x1+μM(x2)/x2+…+μM(xn)/xn,其中，μM表示模糊集M的关系函数，即μM:X→[0,1],μM(xi)(i=1,2,…,n)表示xi隶属于模糊集M的关系度.如果∃xi∈X使得μM(xi)=1，那么模糊集M被称为标准模糊集.由文献可知,[12]如果论域X上的模糊集既是标准模糊集又是凸集，那么它就是一个模糊数.

论域X下的三角模糊数可以被表示成一个三角关系函数M=(l,m,u;wM),其中,wM∈(0,1].l,m和u都是实数，l和u分别是模糊数M的上界和下界，m为最可能取的值,l≤m≤u.当wM=1时，三角模糊数M称为标准三角模糊数.当l=m=u且wM=1时，M就是一个精确数.三角模糊数的几何解释如图5所示.

图5 三角模糊数的几何解释

一个标准三角模糊数M的关系函数如下所示：

(1)

若M1=(l1,m1,u1)，M2=(l2,m2,u2)为两个三角模糊数，⊕、⊖分别代表模糊加法和模糊乘法算子，模糊数的运算法则如下：[13]

模糊数的加法：

M1⊕M2=(l1,m2,u2)

=(l1+l2,m1+m2,u1+u2)，

(2)

模糊数的乘法：

M1⊗M2=(l1,m1,u1)⊗(l2,m2,u2)

=(l1l2,m1m2,u1u2)，

(3)

模糊数的倒数：

(4)

模糊数的数乘：

K⊗M1=(Kl1,Km1,Ku1),K∈R,K≥0.

(5)

2.2.2 三角模糊判断矩阵

用FAHP法确定指标权重，首先要确定语言变量的三角模糊数.文献在Saaty教授1-9标度法的基础上，[14]采用三角模糊数表示语言变量的隶属度函数，用数字来表示指标间的“相对重要性”，如表1所示.

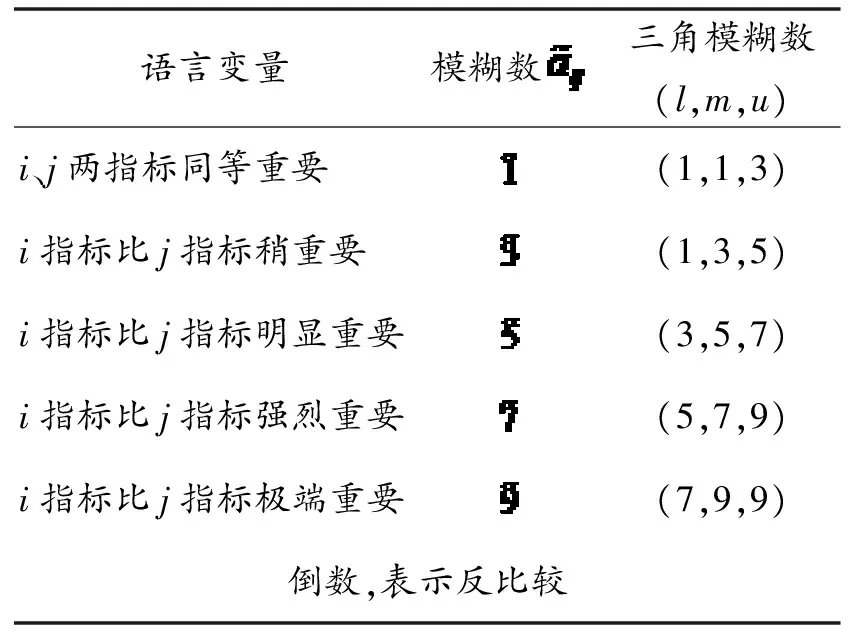
表1 语言变量的隶属度函数

FAHP中判断矩阵的每一个元素都是三角模糊数，然后通过这些三角模糊判断矩阵来求解评价指标的三角模糊权重.

定义2 设A=(aij)L×L(i,j=1,2,…,n)是一个L×L维的判断矩阵，如果该矩阵中的每一个元素aij都是一个三角模糊数，即aij=(lij,mij,uij)，其中0≤lij≤mij≤uij.那么，称该矩阵是一个三角模糊判断矩阵，其中，L是所有评价指标的个数.

定义3 设A1,A2,…,At,…,AT为T个三角模糊判断矩阵，它们分别由T位专家给出，其中At表示第t位专家给出的关于指标重要性程度的三角模糊判断矩阵，即

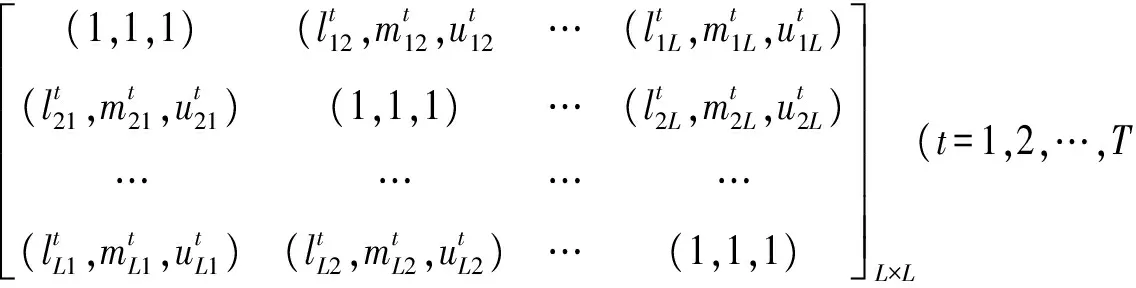
(6)

2.2.3 三角模糊权重的集结

(1)确定模糊指标权重

运用几何平均值法综合t位专家的模糊判断矩阵，得到综合模糊判断矩阵A=[aij]，其中：

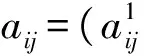
(7)

确定i指标相对同层各指标(共L个)的模糊比较值，ri=(ai1⊗ai2⊗…⊗aiL)1/L

(8)

计算i指标的模糊权重，

wi=ri⊗(r1⊕r2⊕…⊕rL)-1

(9)

记为wi=(lwi，mwi,uwi),其中lwi,mwi,uwi分别表示i指标模糊权重的下限、最可能取的值和上限.

(2)指标权重的标准非模糊化

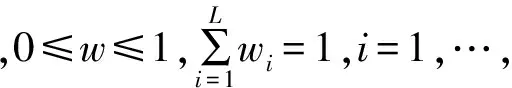
BNPwi=[(uwi-lwi)+(mwi-lwi)]/3+lwi,∀i

(10)

假设指标层θ有L个指标，则第i个指标的权重wi的标准BNP值为：

(11)

由公式(11)计算出的标准BNP值，作为权重引入下文的ER算法中.

2.3 ER算法与步骤

Yang和Xu研究了基于D-S理论的ER方法在具有不确定性的多属性决策问题中的应用,[16]在已有的不确定性证据推理方法的基础上，本文提出了将证据推理方法中确定的指标权重推广到三角模糊数，并用此改进的ER方法解决绩效评估中的主观性和不确定性.

2.3.1 基本的证据推理模型

定义指标集E=(e1,…，ei,…el)，并估计相应权重w=(w1,…,wi，…,wi)，并满足

定义评价等级集合H=(H1,…，Hi,…，HN).

定义评价对象at(t=1,2,…，M)关于指标ei(i=1,2,…,L)的分布S(ei(ai))={(Hn,βn,i(at)),n=1,2,…,N},(t=1,2,…,M)

(12)

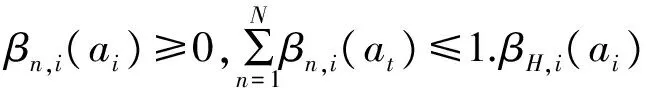
mn,i(ai)为方案at的第i个指标ei在语言评价等级Hn上的基本可信度分配，mH,i(at)为方案at在第i个指标ei上的不确定的基本可信度分配.算法如下：

mn,i(at)=wiβn,i(at)，i=1,2,…，L，t=1,2,…M，n=1,2,…,N

(13)

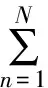
(14)

(15)

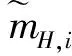
(16)

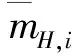
(17)

Hn∶mn,I(i+1)(at)=KI(i+1)，i=1,2,…，L-1，

(18)

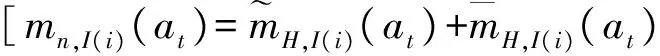
(19)

(20)

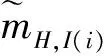
(22)

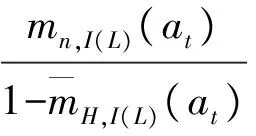
(23)

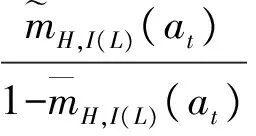
(24)

2.3.2ER方法求解总效用值

为了进行方案的比较和筛选，必须将每个at的总置信度转化为效用值：

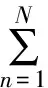
(25)

若专家对一个方案的某个或若干个属性的原始评价含有不确定信息，则根据证据合成公理4,[16]合成后所得的总置信度也是不确定的，即βH(at)≠0.因此，Yang定义了最大效用值umax，最小效用值umin和平均效用值uavg来计算不确定平均中某一被评价方案的效用值，计算公式如下：

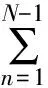
(26)

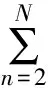
(27)

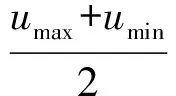
(28)

基于效用值可对评估对象排序.称at优于ak当且仅当umin(at)gt;umax(ak)，称ai和ak无差别，当且仅当umin(at)=umin(ak)且umax(at)=umax(ak).对其他情况，则根据平均效用排序.

3 基于FAHP和ER的计算机平台评估及分析

3.1确定指标权重

组成由专家和学院教师组成的三人评估小组，基于三位专家给出的判断矩阵，运用公式(7)-(11)得到指标权重为：

w1=0.1883,w2=0.1627,w3=0.2557,

w4=0.1447,w5=0.2486,w11=0.2797,

w12=0.3149,w13=0.1224,w14=0.1831,

w15=0.0999，w21=0.5847,w22=0.1661,

w23=0.2492,w31=0.4279,w32=0.5721,

w41=0.5,w42=0.5,w51=0.6481,

w52=0.1105,w53=0.2414.

3.2确定指标的评价体系

评估小组通过讨论定义计算机平台综合绩效的评价等级集合为，H={很差(H1)，差(H2)，一般(H3)，好(H4)，很好(H5)}，得到如表2所示的评价结果.

表2计算机平台绩效的第二层指标评价表(评价值已经过转换)

一级指标二级指标A1A2A3e1e2e3e11e12e13e14e15e21e22e23e31e32H3(0．7)H4(0．3)H2(0．3)H3(0．7)H3(0．3)H4(0．7)H4(1)H2(0．7)H3(0．7)H4(0．3)H2(0．7)H2(0．3)H4(0．7)H3(1)H2(1)H3(0．3)H4(0．7)H4(1)H2(0．7)H4(0．3)H2(0．3)H4(0．7)H4(0．7)H3(0．3)H4(0．7)H2(0．7)H4(1)H5(1)H3(1)H4(1)H3(1)H3(0．7)H4(0．3)H1(0．3)H3(0．7)H3(0．7)H2(0．3)H3(0．7)H3(0．7)H3(1)H4(1)H5(1)

一级指标二级指标A1A2A3e4e5e41e42e51e52e53H2(0．2)H3(0．8)H3(0．8)H3(0．2)H4(0．8)H2(0．4)H3(0．6)H3(0．9)H3(0．4)H4(0．6)H3(0．9)H1(0．2)H2(0．8)H2(0．3)H3(0．7)H3(0．9)H3(0．1)H4(0．9)H4(0．9)H2(1)H2(0．2)H3(0．8)H2(0．9)

3.3计算总置信度和总效用值

我们通过智能决策系统软件(IDs)，[16]对此评估过程中的证据融合进行了模拟仿真.该软件可以对具有精确值权重和精确值置信度的MCDM问题进行证据融合，得到被评价方案在各个评价等级上总的置信度以及总效用值.在这里设总识别框架中评价等级的效用值为：

U(H)={u(H1),u(H2),u(H3),u(H4),u(H5)}={0,0.25,0.5,0.75,1.0}得到的结果如表3所示为.

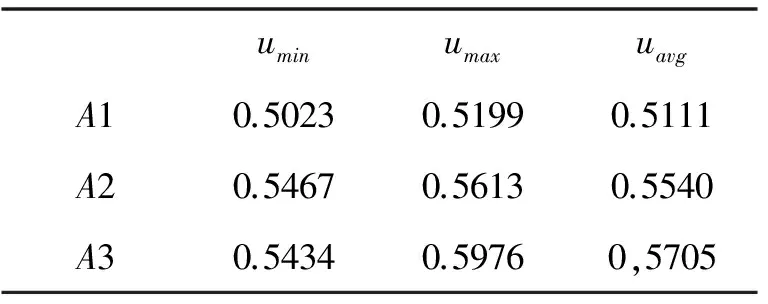
表3 三个被评估平台的效用值

由表3和2.3节描述的排序规则得到，三个被评估平台的综合绩效的优先序为A3gt;A2gt;A1，即在三种计算机平台中，云平台的综合绩效好于其它两个平台.

4 结语

随着我国高等院校职业化教育的发展，使用何种技术建设高等院校的计算机平台已成为重要问题.本文从定量与定性相结合的角度,建立了一个基于FAHP和ER的多属性决策模型，并将该模型应用于高校计算机平台评估中，分别对传统平台、虚拟化平台和云平台的综合绩效进行了评估.根据评估小组给出的评估结果进行分析和计算，得到三个被评估平台的优先序为A3gt;A2gt;A1，即云平台的综合绩效好于传统平台和虚拟化平台，为推广云平台技术在各高校计算机平台建设中的应用提供了必要的理论依据.

本文将模糊信息引入到不确定环境下基于ER的MADM方法中，使用FAHP方法得到指标权重，为如何将模糊方法与ER相结合，以解决专家判断时的不确定性和模糊性做出了初步尝试.但是，本文在实证研究中，选用专家数较少，因此评价结果的决策价值仍需要考证.其次，证据融合过程中的模糊信息集结问题也需要进一步研究.

[1] 史佩昌，王怀民，蒋 杰，等.面向云计算的网络化平台研究与实现[J].计算机工程与科学,2009(S1)：249-252.

[2] 赵 钧.构建基于云计算的物联网运营平台[J].电信科学，2010(6)：13-15.

[3] 吴吉义，平玲娣，潘雪增，等.云计算：从概念到平台[J].电信科学，2009(12)：1-11.

[4] 张 敏，陈云海.虚拟化技术在新一代云计算数据中心的应用研究[J].广东通信技术，2009(5):35-39.

[5] 周 谧.基于证据推理的多属性决策中若干问题的研究[D].合肥:合肥工业大学硕士学位论文，2009：35-38.

[6] 周冠宇.云计算的虚拟技术架构分析[J].移动通信，2011(9)：9-13.

[7] Cloud computing[EB/OL].http://en.wikipedia.org/wiki/Cloud_computing,2011-12-03/2011-12-06.

[8] 智慧的地球—IBM 动态基础架构白皮书[EB/OL].http://www.ibm.com/cn/express/migratetoibm/dynamicinfrastructure/download/dynamicinfrastructure_whitepaper_0903.pdf,2011-12-08.

[9] 李刚健.基于虚拟化技术的云计算平台架构研究[J].吉林建筑工程学院学报，2011(1)：79-81.

[10]单汨源,张 丽,吴 娟.基于RAGA—AHP法的项目优先级评定研究[J].科技管理研究,2008(3):271-274.

[11]Bucaley J.FuzzyHierarchicalAnalysis[J].Fuzzy Sets Syst,1985(1):233-247.

[12]Chen S M, Wang C H.FuzzyRiskAnalysisBasedonRankingFuzzyNumbersUsinga-cuts,BeliefFeaturesandSignal/noiseratios[J].Expert Systems with Applications,2009(3):5576-5581.

[13]Chen S J, Hwang C L.FuzzyMultipleAttributeDecisionMaking,MethodsandApplications[C]//Lecture Notes in Economics and Mathematical Systems, New York: Springer,1993:375.

[14]Chiou H K, Tzeng G H.FuzzyHierarchicalEvaluationwithGreyRelationModelofGreenEngineeringforIndustry[J].Int J Fuzzy Syst,2001(3): 66-75.

[15]Wu H Y, Tezng G H, Chen Y H.AfuzzyMCDMApproachforEvaluatingBankingPerformanceBasedonBalancedScorecard[J].Expert Systems with Applications,2009(6):135-147.

[16]Yang J B, Xu D L.OntheEvidentialReasoningAlgorithmforMultipleAttributeDecisionAnalysisunderUncertainty[C]//IEEE Transaction on System,Man and Cybernetics,2002(3):289-30

[责任编辑唐华生]

EvaluationofComputerTrainingPlatformBasedonFAHPandER

FU Jian-min1，LIU Yin2, SONG Bei-bei1

(1. Computer Science and Technology Department of Anhui Industry and Economy Technical and Vocational College, Hefei Anhui 230051,China; 2. Resource and Environment Engineering of Hefei Industry University, Hefei Anhui 230009, China)

The choices of computing platform affect the development of college occupation education directly. This paper extended the index weight， which in the evidence reasoning method， to triangular fuzzy number. It built a Multiple Attribute evaluation model concerning both of quantitative and qualitative. What's more, it certified that cloud platform is better than traditional platform and virtual platform. Firstly, this paper introduced the concepts of cloud, traditional and virtual platforms. Secondly, it pointed out the computer platform evaluation model based on FAHP and ER, which considering the fuzziness and uncertainty in the decision-making process. At last, it uses the preceding model to estimate the synthesized performances of the three platforms and proved the effectiveness and advancement of this model and the cloud platform.

cloud platform;multiple attribute decision making;fuzzy hierarchy analysis method; evidence reasoning

2012-11-26

中石化海相前瞻性项目(YPH08112)；安徽省教育厅高校自然科学研究项目“云计算在地质矿产勘查中的应用”(KJ2011B22)；安徽省教育厅高校教学质量与教学改革工程项目(20110146)

付建民(1954—)，男，河北藁城人.副教授，硕士，主要从事计算机网络及应用研究.

TP399

A

1674-5248(2013)02-0061-07