假设检验与区间估计的关系问题

王凡彬

(1.内江师范学院 数学与信息科学学院,四川 内江 641100；2.四川省高等学校数值仿真重点实验室，四川 内江 641100)

假设检验与区间估计的关系问题

王凡彬1，2

(1.内江师范学院 数学与信息科学学院,四川 内江 641100；2.四川省高等学校数值仿真重点实验室，四川 内江 641100)

纠正了现行教材中的关于假设检验与区间估计关系问题的错误，给出了二者正确的关系，丰富并发展了其结果．

假设检验；区间估计；关系

0 引言

概率论与数理统计广泛应用于工农业生产和科学实验中．[1-5]由于在假设检验中所用的检验统计量与区间估计中所用的枢轴量是相同的，因此二者存在非常密切的关系．教材[1]在讨论单个正态总体均值的检验时，针对第三类检验问题即双侧检验问题H0∶μ=μ0，H1∶μ≠μ0,对水平为a的假设检验与区间估计的关系讨论得很好．但在讨论水平为a的第一类假设检验问题

H0∶μ≤μ0,H1∶μgt;μ0

(1)

与参数μ的1-α的置信上限的关系时，发生了错误．本文针对教材[1]的错误，进行了纠正，给出了二者的正确关系，并把结果进行了推广．

1 现行教材的错误及纠正

设x1,x2,…,xn是来自正态总体N(μ,σ2)的样本．教材[1]认为，对第一类假设检验问题(1)(单侧检验问题)，其水平为a的检验的接受域为

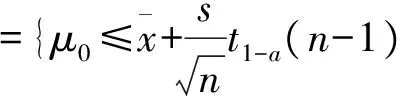
(2)

(3)

得到的应该是参数μ的1-a置信下限而非置信上限．教材[1]所说的“接受域”实际既非接受域也非拒绝域．那么，教材[1]错在什么地方呢？

事实上，由于t分布是对称分布，注意到ta(n-1)=-t1-a(n-1)，那么

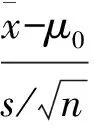
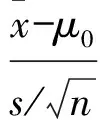
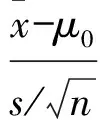
=1-a.

(4)

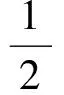
同样，从水平为a的接受域出发，μ的第二类检验问题

H0∶μ≥μ0,H1∶μlt;μ0

(5)

与μ的1-a置信上限才是一一对应的，而不是教材[1]所说的与置信下限一一对应．

2 结果的推广

从上面的讨论我们看到，由于t分布是对称分布，从概率相等的角度，未必一定要μ的第一类检验问题(1)与μ的1-a置信下限一一对应；μ的第二类检验问题(5)与μ的1-a置信上限一一对应．实际上，从μ的第一类或第二类检验问题出发，均可得到μ的1-a置信上限和置信下限．反之，从μ的1-a置信上限或置信下限出发，也可以得到μ的水平为a的第一类和第二类检验问题．

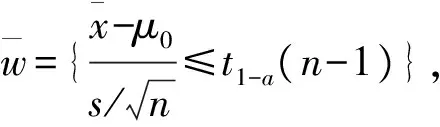
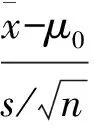
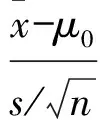
=1-a.

(6)

即

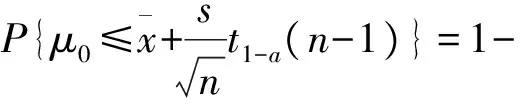
(7)

这就得到了μ的1-a置信上限．

同理，从μ的第二类检验问题(5)的接受域出发，注意到ta(n-1)=-t1-a(n-1)，有

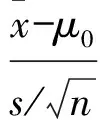
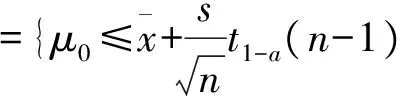
(8)

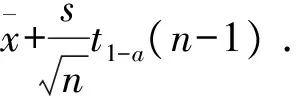
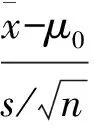
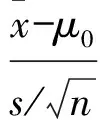
=1-a.

(9)

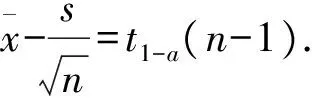
这就完成了第一个方面的推广．

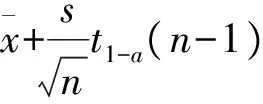
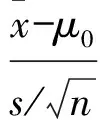
=P{t≥ta(n-1)}

=P{t≤t1-a(n-1)}=1-a.

(10)

从而

P{t≥t1-a(n-1)}=P{t≤ta(n-1)}=a.

(11)

注意到上式给出了拒绝域，这样我们分别得到μ的第一、二类假设检验问题(1)和(5)．

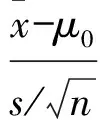
=P{t≤t1-a(n-1)}

=P{t≥ta(n-1)}=1-a.

(12)

由(12)可得(11)，从而也能分别得到μ的第一、二类假设检验问题(1)和(5)．

这就完成了第二个方面的推广．

3 结论

从第2节的讨论可以看出，假设检验与区间估计的关系是：从μ的水平为a的第一或第二类检验问题可以得到μ的1-a置信上限和下限；反之，从μ的1-a置信上限或下限也可以得到水平为a的第一和第二类假设检验问题．这样，就大大丰富和发展了教材[1]的结果．

[1] 茆诗松，程依明，濮晓龙．概率论与数理统计教程[M]．北京：高等教育出版社，2012:335-345．

[2] 王凡彬．一个社会问题的概率方法研究[J]．四川文理学院学报，2011(5)：7-8．

[3] 王梓坤．概率论基础及其应用[M]．北京：科学出版社，1979:232-234．

[4] 复旦大学．概率论：第2册[M]．北京：人民教育出版社，1980:197-202．

[5] 浙江大学数学系．概率论与数理统计[M]．北京：高等教育出版社，1985:257-267．

[责任编辑邓杰]

RelationshipbetweenHypothesisTestingandIntervalEstimation

WANG Fan-bin1, 2

(1. Mathematics and Information Science College of Neijiang Normal University, Niejiang Sichuan 641100，China; 2. Key Laboratory of Numerical Simulation in the Sichuan Province College, Neijiang Sichuan 641100,China)

Existing textbooks on hypothesis testing and interval estimation of the relationship between the error was corrected, both the right relationship is given, and the result has been enriched and developed.

hypothesis testing; interval estimation; relationship

2012-09-12

内江师范学院重点科研项目(09NJZ-1)；四川省高等学校数值仿真重点实验室重点科研项目(09NJZZ001)

王凡彬(1957—)，男，四川富顺人.教授，主要从事偏微分方程及应用研究．

O212.1

A

1674-5248(2013)02-0007-03