基于定位孔垂直度公差的定位销高度计算方法研究

刘 平，姜自莲

(成都工业学院 工程素质训练中心，成都 610031)

姜自莲(1972- )，女(汉族)，四川广安人，副教授，硕士，研究方向：机料加工工程。

基于定位孔垂直度公差的定位销高度计算方法研究

刘 平，姜自莲

(成都工业学院 工程素质训练中心，成都 610031)

以工件定位孔垂直度误差对定位销定位高度的影响为出发点，经过细致的理论分析和比较，在借鉴现有夹具设计理论的基础上，建立了基于工件定位孔垂直度公差的短定位销高度计算方法；为解决长期困扰夹具设计中关于长、短定位销高度的量化问题探索出了一种准确可靠、简便易行的方法。

定位销；高度；垂直度；自由度；夹具设计

定位元件是构成机床夹具最基本、最重要的构件，其作用是限制工件自由度。在实际生产加工中，工件常以孔作为定位基准在圆柱定位销上定位。根据夹具设计的相关理论[1]，当定位孔在长定位销上定位时，工件上有4个自由度被限制；定位销为短定位销时，则只限制工件的2个自由度。如果工件在定位时只需要短销而误用长销定位，就会产生“过定位”，使工件不能正确安放；反之，需要长销而误用了短销，就会产生“欠定位”，使工件的位置不确定。由此可见，短销的最大定位高度HO是区分长销和短销的特征参数：当定位销定位高度HX≤HO时，定位销为短销；当HXgt;HO时则为长销。因此，确定定位销的定位高度是设计定位销时不能回避的问题，然而到目前为止，还没有一个准确、可行的方法来计算、确定HO。本文从工件定位孔垂直度误差对定位销高度的影响出发，建立基于工件垂直度公差的HO计算方法。

图1 工件坐标系

图2 定位销高度的计算简图

图3 工件简图

1 短定位销最大允许高度的影响因素与存在条件分析

1.1 短定位销最大允许高度的影响因素

(1)

式中：HO为定位销的最大高度/mm；L为工件定位孔到端面间的距离/mm；D为工件定位孔的最小直径/mm；Δmin为工件定位孔与定位销间的最小间隙，Δmin=D-d(d为定位销最大直径/mm)。

笔者认为该方法存在2点商榷之处：

1)计算结果不一定具有实用价值

显然，直径d=15 mm，高度H=0.779 mm的定位销是没有实际使用价值的。

图4 α=90°时不产生干涉

图5 αlt;90°时产生干涉

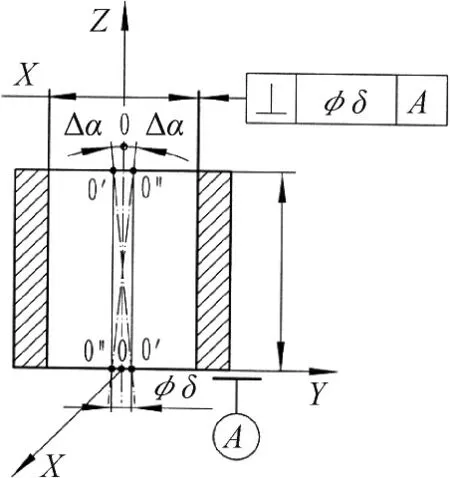
图6 Δα与垂直度公差的关系

2)在理论上存在重大缺陷

分析式(1)和图2可知，该方法没有考虑工件定位孔与定位基面的垂直度误差对定位销高度的影响，这是该方法在理论上存在的重大缺陷。

如图4所示，当工件定位孔与定位基面的垂直度误差为零时，即工件定位孔实际轴线与基准平面的夹角α=90°时，只要Δmin≥0，即使HXgt;HG造成过定位也不会产生干涉而影响工件的定位，且不受工件定位孔到端面间的距离L的影响。

反之，如图5所示，当αlt;90°时，即使HXlt;HG，也可能产生过定位并且产生干涉，使工件的定位不能达到预期的效果，造成工件的装夹变形，最终影响工件的加工质量。由此可见，工件定位孔与定位基面的垂直度误差是影响定位销高度的关键因素。因此，在工件定位孔垂直度公差一定的条件下，要消除过定位，必需确定HO且让HX≤HO。

综上所述，建立计算HO的计算方法，必须基于工件定位孔与定位基面之间的垂直度公差。

1.2 短定位销最大定位理论高度HO的存在条件

1.2.1 基准转角误差Δα

1.2.2 定位转角误差Δθ

定位转角误差Δθ是指定位销高度为HX、孔与销的配合间隙为Δmin时，定位孔绕X轴或Y轴转动的最大转角位转角误差。显然，Δθ是定位孔被定位销约束后，理论上允许其轴线绕X轴或Y轴“转动”的最大角度。

1.2.3 短定位销最大理论高度HO成立的条件

因此，要使短定位销成立，必须满足2个条件：

图7 Δθ与HX和Δmin的关系

图8 HO计算简图

1)Δmingt;0

(2)

2)Δθ≥Δα

(3)

根据上述条件，Δmin必须大于零，孔上定位后才有绕X轴或Y轴转动的空间，而且Δmin越小，Δθ也越小；另一方面，如图8所示，当定位销高度为HX1时，对应的定位转角误差为Δθ1；定位销高度为HX2时，对应的定位转角误差为Δθ2(图中用双点划线绘出)，比较可得：HX1lt;HX2时，有Δθ1gt;Δθ2。该规律表明定位孔绕X轴或Y轴转动角度与定位销高度HX的关系：Δmin相同时HX越小，Δθ越大。因此，当Δmin确定以后，必然存在一个定位销高度使Δθ=Δα成立，该定位销高度即为HO。

2 短定位销最大高度的理论公式及设计方法

2.1 短定位销最大高度HO的理论公式

根据上述分析可知：当Δθ=Δα时，对应的短定位销高度即为HO。为了便于建立HO的计算公式，绘出了HO的计算图如图8所示。

由于Δθ=Δα必然有：

tanΔθ=tanΔα

(4)

由图8所示几何关系得：

(5)

表1 定位销的HXmin参考值

注:数据均参考资料[1]并结合经验确定

(6)

将式(5)和式(6)代人式(4)得：

(7)

由式(5)即解得HO的计算公式：

(8)

2.2 短定位销计算设计方法

2.2.1 短定位销的最小结构高度HXmin

分析式(8)可知，由于HG、δ均为工件设计参数，一般不能改变，当Δmin很小时HO值也可能很小，因此不具有实际使用价值。所以，有必要规定一个结构上需要的最小高度HXmin(参见表1)来确保HO具有实际生产和使用价值。由此可知，在设计短定位销时，其高度HX应满足式(9)。

HO≥HX≥HXmin

(9)

2.2.2 短定位销设计步骤

1)应用式(8)计算最大理论允许高度HO。

2)校核HO能否实际使用。将计算所得的HO与HXmin比较，若满足式(9)则可按式(11)确定HX；反之，则进行修正计算。

2.2.3 短定位销高度的修正计算

修正计算的方法是：减小定位销最大直径d至d'，同时将Δmin扩大为Δ'min，以保证高度由HO加大到HXmin时，仍能满足Δθ=Δα的要求(见图9)。将Hmin作为已知条件代入式(9)可得Δ'min和d'的计算公式：

(10)

d'=D-Δ'min

(11)

式中：D为工件定位孔的最小直径；d' 为定位销修正后最大直径，其公差在h5、h6、h7等公差带中选择。

具体计算步骤为：1)根据工件定位孔直径，查表1选定HXmin；2)利用式(10)计算Δ'min；3)利用式(11)计算短定位销的最大直径d'；4)确定定位销直径公差。

图9 短定位销的高度修正计算

图10 工件定位简图

3 计算方法应用示例

3.1 计算定位销最大高度HO

1)按标准配合计算Δmin

Δmin=12-(12-0.006)=0.006 mm

2)计算HO

将已知参数代入式(8)得：

查表1得，HXmin=3 mm，因为HOlt;HXmin不满足式(9)，故需要进行修正计算。

3.2 对HX进行修正计算

1)计算Δ'min

2)计算定位销最大直径d'

根据式(11)，d'=D-Δ'Xmin=12-0.015=11.985 mm

3)定位销公差的确定

4 结语

本文提出并分析了基于工件垂直度的短定位销长度H的计算方法，解决了长期困扰夹具设计与教学领域的短定位销长度难以确定的问题。笔者认为该方法具有简便易学，计算结果可靠等优点，具有在夹具设计和教学中应用与推广的价值。

[1] 王光斗,王春福.机床夹具设计手册[M].3版.上海:上海科技出版社,2000.

[2] 方昆凡.公差与配合实用手册[M].2版.北京:机械工业出版社,2012.

[3] 杜官将.定位销高度的确定[J].机械工程师,1998(6):35.

[4] 孙千里,沈鑫刚.“一面两孔”定位销实用设计方法与结构[J].机械科学与技术,2010(12):1703-1705.

[5] 石怀荣.基于夹具设计中定位销长度的分析[J].机电工程,2005(7):54-56.

ResearchonCalculatingMethodofLocatingPinHeightsBasedontheTolerancesofPerpendicularityforLocatingHoles

LIUPing，JIANGZiliang

(Engineering Trainging Center,Chengdu Technological University，Chengdu 610031， China)

Based on the reality of fixture design， in conformity with the principle of accuracy ，reliability， simplicity and learnability， this article aims at establishing calculating method of short locating pin heights based on perpendicularity in workpieces.

Locating Pin；height；perpendicularity；freedom；fixture design

2012-12-27

刘平(1955- )，男(汉族)，四川成都人，高级工程师，研究方向：机械设计与制造。

TH131

A

2095-5383(2013)02-0032-04