基于Hadoop的QR树索引方法

冯 钧，任 锋，唐志贤

（河海大学 计算机与信息学院，江苏 南京211100）

0 引 言

随着信息技术的迅猛发展，各种高新技术应用会周期性地生成海量的空间数据[1]。因而组织和使用这些数据显得愈发的重要。空间数据通常形式多样、规模巨大、计算复杂。这些特性使得如何深度地利用空间数据成为一项具有挑战性的工作。高效的数据访问是深度利用海量数据的前提，如何高效地对空间离散数据进行索引以满足日益增长数据应用的的实时性需求以成为数据库领域的一个研究热点[2－4]。

最基本的空间离散数据索引方法是通过将整个空间区域划分成不同的部分，再在各个区域中按照一定的顺序查找数据。典型的primary index有B树、K－D树、K－D－B树、四叉树、R树及其变体[5，6]等等。在海量空间数据的情况下，往往导致树的深度过深，上述结构的检索效率明显较低。secondary index作为一种混合式索引结构，常见的有QR树[7]、PMR树[8]、Hilbert R树[9]等等，通过两级级索引的方式能够有效降低树的深度，提高检索效率，但是由于结构复杂，在处理海量数据时会带来庞大的计算量。面对海量空间数据处理与查询的复杂性，传统的集中式处理方式已经变成制约处理和查询效率的 “瓶颈”。随着 “云计算”的兴起，其所具有扩展性好、容错性强同时具有强大的数据并行处理能力的特点，为突破上述 “瓶颈”提供了一个很好的思路[10]。Hadoop[11]是由 Apache基金会开发的开源分布式架构，结合MapReduce能够对海量空间数据以一种可靠、高效、可伸缩的方式进行处理。

本文提出一种基于Hadoop的QR Tree分布式空间索引，索引存储在HDFS文件系统中的空间数据；利用四叉树对索引空间的分层划分，减少R树空间重叠和查找失败路径，有效的解决数据非均匀分布时的不平衡问题。借助Hadoop平台强大的MapReduce并行编程框架设计相应的数据处理算法，改善索引建立过程，提高查询过程的效率。

1 Hadoop QR Tree索引结构设计

逻辑结构

基于Hadoop的QR树将四叉树与R树结合起来。它通过四叉树将整个空间划分成至多个子空间 （k为空间维度）。四叉树的每个节点对应一个独立的R树。R树通过其最小外包矩形 （MBR）确定所属四叉树节点。空间数据都存储在R树中。假设四叉树节点的最大容量为Vmax，即各个子空间中数据量最大为Vmax。当某数据空间中数据量超过Vmax时，需要进行分裂。假设图1（a）中数据量超过子空间最大容量Vmax，本文使用四叉树将原数据空间划分为5个子空间。如图1（b）、图1（c）所示，原空间中数据根据其空间位置划归到各子空间中。若原空间中有数据与多个下层子空间有交集，则将其划分到上层子空间[12]。

Hadoop QR Tree（HQR Tree）索引支持离散数据查询和区域查询。HQR Tree利用四叉树将整个索引空间分成多个子空间，并分别为每子空间中的数据建立R树，不同子空间中空间数据彼此无交集。

如图2所示的是一棵二维空间的QR树，空间区域内包含多个空间数据 （包括点数据和面数据）。图2中QR树的高度为4，有14个R树。整个空间区域被划分成20个子区域，共有四层:S1，S2，S3……S20。其中S0＝S1∪S2∪S3∪S4，S1＝S5∪S6∪S7∪S8等。同时有20棵R树R1，R2，R3……R20，每课R树都对应一个子空间。每个四叉树节点包含的子空间均由其上层节点所包含的空间分裂而来。当上层节点的中数据量超过节点最大容量时，需要分裂。以空间S1为例，S1中数量超过最大容量，使用四叉树将S1划分成S5，S6，S7，S8这5个子空间。空间区域上，S5，S6，S7，S8彼此无交集，且S1与原空间区域大小相同，为S5，S6，S7，S8空间区域之和，同时S5，S6，S7，S8在四叉树中作为原节点的新增孩子节点存在，而S1取代原节点。原空间中数据根据空间位置插入子空间S5，S6，S7，S8中，若有数据同时与S5，S6，S7，S8中多个有交集，则插入S1中。数据r1落在子空间S5中且不与其他子空间相交，则r1被插入到R5中；而r2与S1，S5，S6，S7，S8相交，根据上述空间分裂规则，插入子空间S0中，因此数据r11被插入到中。

2 基于MapReduce并行创建索引

索引创建算法

本文利用MapReduce改造索引创建算法。基本思想:首先用四叉树将索引空间划分成个子空间，建立一棵四叉树，四叉树的每个节点都对应一棵R树，当四叉树节点对应子空间数据超过最大容量时将导致节点分裂。将数据的MBR与各子空间比较，寻找能够完全将其包含的最小子空间，将数据映射到该子空间。若子空间达到最大容量，则进行分裂。最后，为每个子空间分别建立R树。数据空间的划分和各个子空间R树的建立过程由Map函数实现，完成后返回相应信息，由Reduce函数将各个R树合并起来并挂载到四叉树节点上，最终形成一个全局的QR树。

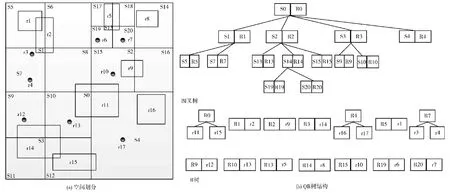
图2 QR树空间划分和树结构

3 分布式并行查询策略

3.1 离散数据查询

基本思想:首先将给定的离散数据数据分组，根据每个空间数据的空间位置判断是否在索引空间中。自上而下查询HQR－tree，与各四叉树节点比较，寻找完全包含数据的最小四叉树节点，接着从此节点对应的R树中查询数据。

3.2 区域查询

基本思想:根据待查询区域空间信息查询索引空间中存在数据。自上而下查询 HQR－tree，与各四叉树节点比较，寻找出与待查询区域相交的四叉树节点，接着从这些节点对应的R树中查询完全包含在相交区域中的数据。

3.3 索引算法性能分析

假设分布式环境下计算节点个数为N，每个节点所能并行运行的Map函数和Reduce函数最多分别为Mn和Rn。则整个系统最大Map函数数为

遍历四叉树，耗时为τq，遍历R树，耗时为τr；

（1）离散数据

查询待查询数据量为O，划分成若干组，每组最多有S个数据 （S≤O），则有个分组。

1）处理单个分组中每个数据是否在四叉树中所需时间为tQ，有

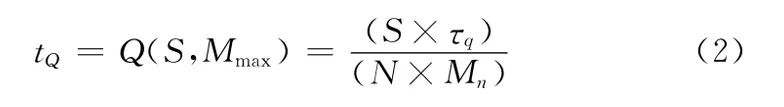
2）处理单个分组中每个数据是否在R树中所需时间为tR，有

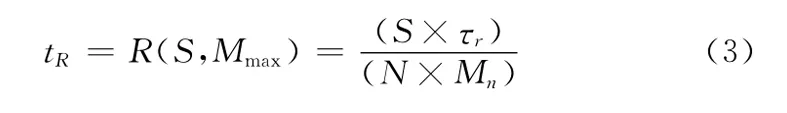
当单次四叉树和R树查询时间不变时，处理时间与每组的数据数S和Map函数个数有关，当S越少同时Map函数个数越多时，处理单个组耗时越少，反之耗时变长。

由上述可得，系统需要顺序执行的Map数Mo为

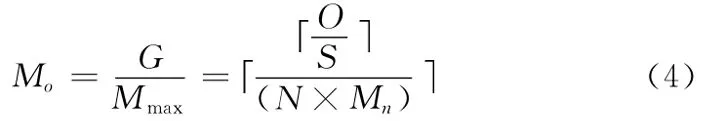
查询O个数据是否在四叉树中耗时

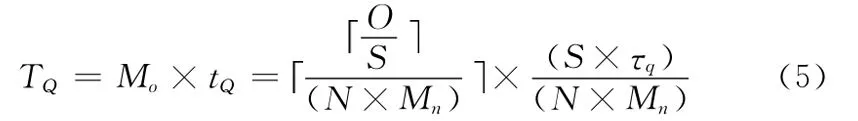
查询O个数据是否在R树中耗时

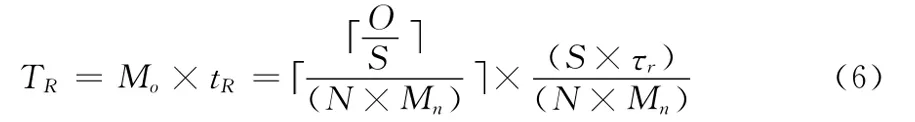
则总处理时间

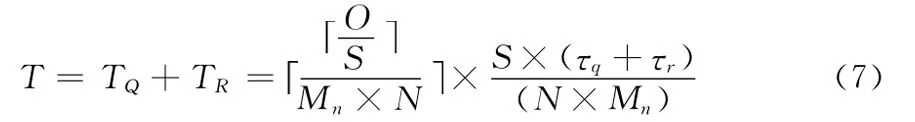
分析上式 （7）可得，相较于集中式索引响应时间O×（τq＋τr），分布式QR树通过分布式环境分散检索的计算量，在数据个数不变的情况下通过增加计算节点来减少查询时间，提高检索效率。

（2）区域查询

与待查询区域相交节点数为Cn，对应Cn棵R树，划分成若干组，每组有S个数据 （S≤Cn），则至少有G＝个这样的分组。

处理单个分组，遍历R树，查询并返回相交区域中数据耗时为

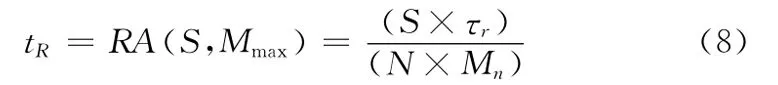
由上述可得，系统需要顺序执行的Map数Ma为

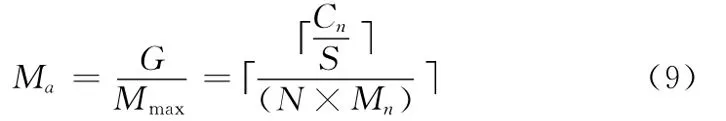
则总处理时间

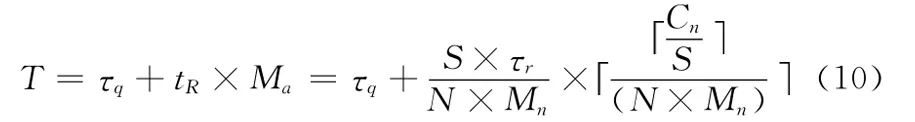
分析上式，当增加计算节点的数量N和每个节点上的Map函数数量Mn时，能够有效减少区域查询的总处理时间T。而在集中式环境下相同条件的区域查询总处理时间为τq＋τr×Cn。相比较可得，在分布式环境下算法查询效率更高。

根据上述对离散数据检索和区域检索的性能分析 （见式 （7），式 （10）），响应时间T与系统计算节点数成正比，当计算节点个数增加时，能够有效的减少响应时间T。HQR－Tree相对于集中式算法能够有效的减少系统响应时间，提高检索效率。

4 索引更新策略

索引空间区域插入或删除数据时，可能带来索引节点的分类或合并。其中节点的分裂和合并包括上层四叉树节点的更新和各四叉树节点对应R树的更新。

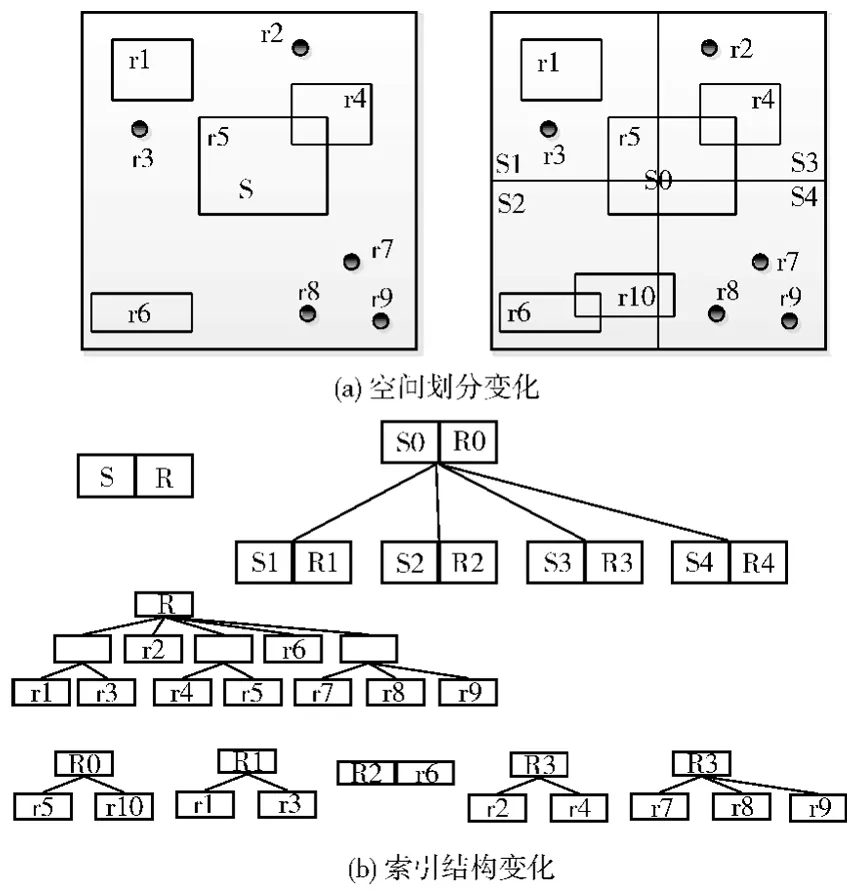
图3 HQR－Tree更新

如图3（a）所示，当空间S中插入新的空间数据r10时，四叉树节点S分裂成S0，S1，S2，S3，S4。相应的空间S所对应的R树将分裂成五个不同的子R树:R0，R1，R2，R3，R4，如图3（b）所示。反之，若删除空间数据r10，则四叉树节点S0，S1，S2，S3，S4合并成一个节点S；同时各四叉树节点对应的R树R0，R1，R2，R3，R4也合并成一棵R树。

（1）数据插入

（2）数据删除

5 实验及分析

5.1 实验环境设置

本实验比较集中式环境下和分布式环境下处理大规模数据。

集中式环境:操作系统:Windows 7；CPU:英特尔酷睿i5－2300CPU ＠ 2.80GHz（单 核）；内 存:1GB ，DDR3，单通道 ；硬盘:希捷ST31000524AS，7200转 ，1000GB。

分布式环境:一台主节点，三台从节点，Ip分别为10.196.80.90／91／92／93。

操作系统均为Oracle Linux Server release 6.3，hadoop版本:1.0.4。其中主节点内存为1G，从节点为1G、1.5G、2G不等。CPU主节点为英特尔单核2.60GHz、从节 点 为 英 特 尔 双 核 3.20GHz、 双 核 1.60GHz、 单核2.66GHz。

实验程序实现:Myeclipse10.6，JDK1.6。

5.2 索引创建

实验采用随机生成的10万、20万、50万、100万、200万、500万、800万、1000万8组空间数据作为实验数据，分别测试在集中式环境下和分布式环境下建立索引所耗费的时间，用以分析比较并行计算和集中式计算的效率。其中四叉树节点容量为512KB。

如图4所示为集中式和分布式环境下创建QR树的对比关系。其中横坐标为实验数据量，纵坐标位创建索引所需的时间。在分析8组随机空间数据可得，在数据量较小时，集中式创建索引较有优势。这是因为，使用分布式计算时，需要花费时间进行数据的分割和计算节点的通信，而单机环境下不存在此问题。但是，当数据量开始变大时，如上实验，当本实验环境下，在数据量超过500万时，分布式环境在为空间数据建立索引时已经开始比集中是创建索引具有优势。此时，随着数据量的增大，计算节点的通信开销及数据分割的开销对建索引效率的影响将越来越低。

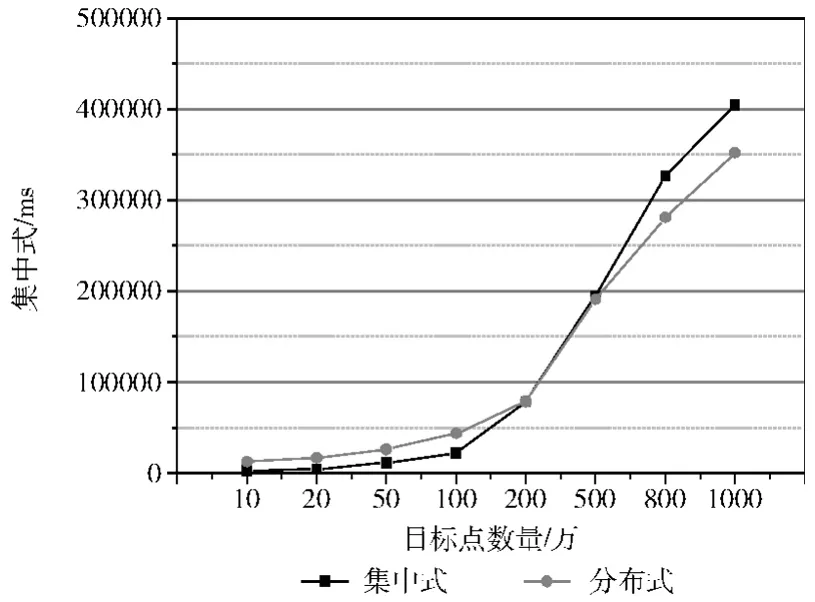
图4 随机数据在集中式环境和分布式环境下建立索引耗时图 （单位:ms）

5.3 随机数据查询

随机数据查询实验采用500万个数据的索引作为实验数据，分别在集中是环境下和分布式环境下进行查询。查询次数为 （单位:次）:10，100，1000，1万，10万，20万，50万，100万。

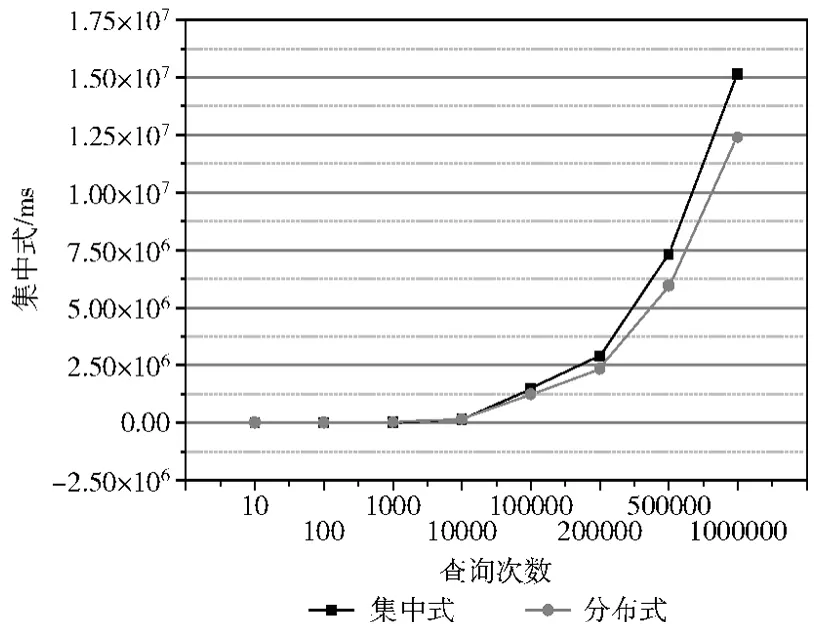
图5 随机数据在集中式环境和分布式环境下查询耗时图 （单位:ms）

图5 所示为随机数据在集中是环境和分布式环境下查询的耗时，其中纵坐标为查询时间，横坐标为查询次数。与建索引时类似，当查询次数较少时，单机查询耗时要小于分布式环境下耗时，但当次数增加到1000次及以上时，分布式环境下的随机数据查询耗时开始优于集中是环境。

6 结束语

HQR－Tree是一种基于Hadoop的分布式QR树索引方法，用于处理海量空间数据。QR树作为两层索引结构结合了四叉树和R树的优点，但由于其结构复杂，创建与维护代价大。通过研究发现，在分布式环境下建立QR树，将计算量分散到各个计算节点中分别处理，可以有效降低算法响应时间，对处理海量空间数据具有良好的表现，大大提高数据处理效率。本文基于Hadoop平台，结合MapReduce的思想，设计优化了分布式环境下QR树索引算法的建立和查询过程 （包括点查询和区域查询）。理论分析与实验结果表明，HQR－Tree的分布式算法在时间复杂度优于QR－Tree。本文的进一步研究将针对HDFS文件系统的特点及动态数据的问题进行设计相应的解决方案进一步优化HQR树性能。

[1]Lee M W，Hwang S.Robust distributed indexing for localityskewed workloads[C]／／Proceedings of the 21st ACM International Conference on Information and Knowledge Management.ACM，2012:1342－1351.

[2]Wang J，Wu S，Gao H，et al.Indexing multi－dimensional data in a cloud system[C]／／Proceedings of the International Conference on Management of Data.ACM，2010:591－602.

[3]Wu S，Jiang D，Ooi B C，et al.Efficient b－tree based indexing for cloud data processing[J].Proceedings of the VLDB Endowment，2010，3 （1－2）:1207－1218.

[4]Zhu M，Shen D，Kou Y，et al.An adaptive distributed index for similarity queries in metric spaces[G].LNCS7418:Web－Age Information Management.Berlin:Springer Berlin Heidelberg，2012:222－227.

[5]Wang J，Wu S，Gao H，et al.Indexing multi－dimensional data in a cloud system[C]／／Proceedings of the International Conference on Management of Data.ACM，2010:591－602.

[6]Wu S，Jiang D，Ooi B C，et al.Efficient b－tree based indexing for cloud data processing[J].Proceedings of the VLDB Endowment，2010，3 （1－2）:1207－1218.

[7]Huang B，Wu Q.A spatial indexing approach for high performance location based services[J].Journal of Navigation，2007，60 （1）:83－94.

[8]Pelanis M，Saltenis S，Jensen C S.Indexing the past，present，and anticipated future positions of moving objects[J].ACM Transactions on Database Systems，2006，31 （1）:255－298.

[9]Zimek A，Schubert E，Kriegel H P.A survey on unsupervised outlier detection in high－dimensional numerical data[J].Statistical Analysis and Data Mining，2012，5 （5）:363－387.

[10]Tanin E，Harwood A，Samet H.Using a distributed quadtree index in peer－to－peer networks[J].The VLDB Journal，2007，16 （2）:165－178.

[11]Apache.Welcome to ApacheTMHadoop ！[EB／OL].[S].[2012－03－19].http:／／hadoop.apache.org／.

[12]GUO Wei.Spatial database indexing techniques[M].Shanghai:Shanghai Jiaotong University Press，2006:129－143 （in Chinese）.[郭薇.空间数据库索引技术[M].上海:上海交通大学出社，2006:129－143.]