移动信标改进的DV-Hop算法
2013-11-30陈志国须文波
陈志国,傅 毅,2,须文波,孙 俊
(1.江南大学 物联网工程学院 轻工过程先进控制教育部重点实验室,江苏 无锡214122 2.无锡环境科学与工程研究中心,江苏 无锡214063)
0 引 言
目前无线传感器网络 (wireless sensor network,WSN)由于灵活性大、容错性强等特点广泛应用于医疗、交通、军事等领域[1]。WSN的应用以数据采集为前提,但 WSN的节点布设随机性强,所以节点如何知道自身位置成为问题的关键和目前的研究热点[2]。
WSN的节点定位一般分为基于测距的 (range-based)定位和无需测距的 (range-free)定位两大类,由于无需额外的硬件,因此实际应用中以后者为主,其中DV-Hop算法备受关注[3]。DV-Hop算法是基于跳数原理的距离无关定位算法,由于后期采用的三边测量法会产生一定的误差,因此一些智能算法逐渐被引入以降低误差,如遗传算法[4]、PSO算法[5]和 QPSO[6]算法改进的 DV-Hop算法。本文将采用一种改进的QPSO算法来降低DV-Hop算法的定位误差。定位精度是WSN的一项重要指标,但节点开销也不容忽视,采用移动信标可以大大降低成本,因此本文还提出了一种基于虚拟力的信标移动新方法来降低系统开销。
1 DV-Hop算法模型
DV-Hop算法的基本原理是先通过计算跳数获得网络拓扑信息,然后用三边定位法获得未知节点信息[7]。跳数计算过程如下:①每个信标节点将自己的位置信息包向外进行广播,初始时跳数为0,收到信息包的节点更新自己的信息表;②继续上一次的广播过程,信息包每转发一次跳数就加1;③节点收到新信息包时先查看自己的信息表里是否已有该信息包的标识,若有且新信息包的跳数值更小,就更新跳数值;否则新数据包被忽略,停止转发。
按照这种规则进行全网内跳数广播,便得到锚节点到其他所有锚节点的跳数和位置。根据位置坐标,锚节点i可以计算出他们之间的距离,然后每一个锚节点按公式 (1)计算平均每跳距离

其中 (xi,yi)是锚节点i的坐标,(xj,yj)是除锚节点i之外的锚节点坐标,hi,j是锚节点i到锚节点j之间的跳数,n是锚节点总数。然后锚节点i向邻居节点广播平均每跳距离,由于数据包里含有锚节点自身标识和平均每跳距离,其他节点收到该数据包时先比对标识,若标识不重复就向邻居节点继续广播,否则丢弃该数据包。这样网络中的每一个节点都知道了所有n个锚节点计算出的平均每跳距离,对这些平均每跳距离取平均值作为自己的每跳平均距离。
之后,未知节点得到了其距离所有n个锚节点的每跳平均距离矩阵和跳数矩阵。对某一个锚节点的跳数与每跳平均距离的乘积就是该节点到锚节点的距离[9],通常采用三边测量法或多边测量法。然后根据最小二乘法原理,求出未知节点的最小二乘位置估计。
由于上述DV-Hop算法采用的三边或多边测量方法会产生较大的误差,为了进一步提高定位精度,这里将引入一种改进的QPSO智能算法对Dv-Hop算法的测量结果进行优化,以提高节点的定位精度。
2 BDQPSO改进DV-Hop节点定位算法
2.1 BDQPSO算法的提出
QPSO算法是J.Sun等人提出的一种改进的粒子群优化 (particle swarm optimization,PSO)算法[10],该算法从量子力学的角度出发对PSO算法的缺点进行改进,具有较好的优化结果,获得了广泛应用。为了进一步提高QPSO算法的收敛精度和全局搜索能力,这里提出一种最佳维改进的 QPSO 算 法:BDQPSO (best dimension quantum-behaved particle swarm optimization)算法。虽然QPSO算法的收敛速度较快,但后期收敛速度会明显变慢,当接近全局最优位置时可能导致粒子停滞在局部最优位置。这里提出一种新的方法,最佳维 (best-dimension,BD)扰动技术,它可以在QPSO迭代时找到最佳维来执行扰动。具体的BD算法流程描述如下:
(2)在选定粒子位置矢量中随机选择s维进行变异,产生s个变异的粒子XM=(XM1,XM2,…,XMs),其中minX)+minX;
(3)从s个变异粒子XM和父代粒子Xit中,选出最好适应度的粒子,计算最好适应度值
为了测试BDQPSO算法性能,用表1的标准测试函数对算法进行分析,同时与QPSO算法进行对比。测试过程中,粒子群数量设定为50,维数设定为10、20、50和80,迭代次数设定为200、500、1000、2000,算法每次独立运行100次,结果见表2。实验环境为:Pentium E5300 2.6 GHZ,2G内存,MATLAB7.04,操作系统为Win7 32位。从表2可见,BDQPSO算法比QPSO算法具有更好的收敛精度,因此更适合于对DV-Hop算法的定位结果进行优化。

表1 标准测试函数
2.2 基于BDQPSO改进的DV-Hop算法
简单的节点定位过程只需要两个步骤,即确定未知节点到锚节点的距离和计算未知节点位置。在第二步中,由于现实环境的不确定性,三边测量或者多边测量方法会产生一定的误差,为了提高定位精度,本文用收敛性更好的BDQPSO算法对DV-Hop算法进行改进。
适应度函数值是评价算法得到的解的优劣程度的标准,这里评价未知节点定位精度的标准是该节点与其他所有锚节点的距离与第一步中由DV-Hop算法得到的距离的累计误差,该误差越小则定位精度越高,该适应度函数表示如下

其中Pi是锚节点位置坐标,n为锚节点数量,xj是未知节点的位置坐标,D(j,i)为未知节点j到锚节点i的距离。f(xj)代表未知节点到所有n个锚节点的距离的累计误差。

表2 标准测试函数测试结果
对DV-Hop算法的改进分为三部分:第一部分用DV-hop算法计算节点间距离;第二部分用多边测量法对第一个模块得到距离计算未知节点的位置坐标;第三部分用BDQPSO算法对第二个模块得到的位置坐标进行迭代优化。改进的DV-Hop算法的步骤如下:
步骤1 每个信标节点将位置信息包 (节点ID、位置坐标 (xi,yi)和跳数hi)进行广播,以获得其它所有锚节点的坐标及跳数距离,然后用式 (1)计算出全网平均每跳距离;
步骤2 每个锚节点广播其计算的平均每跳距离,数据转发过程中也进行跳数计数,各个节点通过上述信息计算出该节点到各个锚节点的距离;
步骤3 利用多边测量法计算出未知节点的位置坐标;
步骤4 将步骤3得到的位置坐标设为BDQPSO算法的初始解,然后开始进行适应度值计算和迭代优化,最终得出更好的结果。
2.3 算法性能分析
为了测试算法性能,拟在100×100的标准矩形区域内,随机布设300个节点,其中30个是锚节点。首先设置节点通信半径为10,锚节点GPS定位误差为0,此时网络的平均连通度为9.0741,网络的邻居锚节点平均数目为0.94276。
实验过程将锚节点比例从1%开始,以2%的增幅增至19%,图1是原DV-Hop算法、PSO改进算法、QPSO改进算法和BDQPSO改进算法的节点定位误差比较结果,实验环境与2.1相同。从图1中可见,随着锚节点比例的增加,BDQPSO改进的DV-Hop算法的定位精度不断提高,定位误差可以达到10%左右,这一结果优于DV-Hop算法和其他几种改进算法。由此可见,在上述3个算法中,提出的BDQPSO改进的DV-Hop算法效果最好,性能最稳定。

图1 锚节点比例与节点定位误差关系
3 改进的移动信标算法
信标节点通过向邻居节点广播自身位置使其他节点完成定位,信标节点的比例越大定位精度越高,开销也越大,为了降低系统开销需要引入移动信标 (mobile beacon)。
移动信标在待检测区域 (region of interest,ROI)内以特定的规则移动并向邻居节点广播自身位置,未知节点据此计算自身位置,移动方法可采用静态或动态方法[11]。
由于WSN传感器节点分布的随机性,这里提出一种静态路径和动态路径相结合的新方法:首先让第一个信标以静态路径在ROI中进行一遍信号覆盖,然后让第二个信标以虚拟力动态路径[12]进行移动,这样既发挥了静态路径的优势,又可以灵活地对剩下的节点进行遍历,提高信号覆盖率。该方法步骤如下:
步骤1 第一个移动信标参考等距三重优化模型以预先确定好的发射位置移动;
步骤2 应用虚拟力,第二个信标进入ROI进行移动:
(1)第二个信标节点以第一个信标节点的相同位置进入ROI,到达m位置时候向邻居节点发射位置信息;
(2)在m位置发射半径内的未知节点收到信息包后,用RSSI算法将损耗功率转化为距离矩阵;
(3)根据人工势场理论[13],第二个信标节点在收到反馈信息后,在m位置计算虚拟力,确定下一个移动位置。
在此过程中有两种情况需要处理:
1)如果第二个信标节点没有收到反馈信息或者受到的虚拟力为0,则信标节点向任意方向移动R/2作为新位置;如果连续移动5次以上受到的虚拟力还是0,则跳出程序;
2)如果计算出的第m+1个发射位置的坐标如果超出了边界范围,则坐标回退到第m个位置并向任意方向前进R/4作为第m+1个发射位置的坐标。
算法的流程图如图2所示。

图2 移动信标算法流程
为了测试算法性能,现在二维空间中进行3组节点定位实验:
第一组是一个移动信标配有GPS定位装置,以静态路径方式移动;
第二组是一个移动信标配有GPS定位装置和一个定向天线阵列,按照虚拟力的引导进行动态路径规划;
第三组有两个移动信标,一个用第一组中的静态路径移动,另一个用第二组中的动态路径移动,假定信标的移动速度不变。
实验条件如下:在100×100的标准矩形区域内,随机部署50个节点,普通节点发射半径为10,循环次数都为15次。这3种方法将在信号覆盖率、发射位置数量以及移动路径长度方面进行比较。
图3显示了3组实验中没有被覆盖的节点数量比较图,第一组实验结果较好,未得到3个非共线锚节点信号的未知节点数量较少。第二组和第三组实验得到的结果差别不太大,但第三组得到的信号未完成覆盖的节点数相对来说最少。
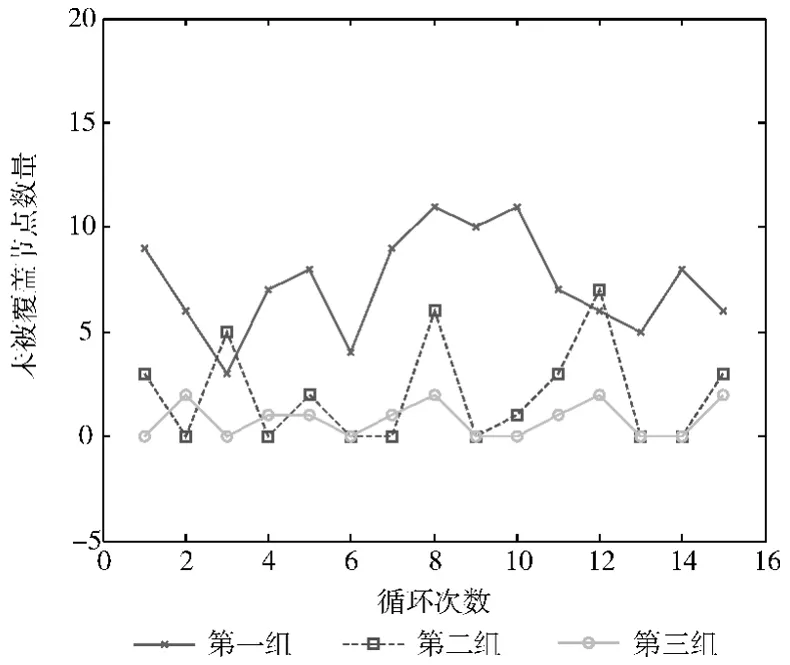
图3 信号未完全覆盖节点数量对比
图4 显示了发射位置数量的对比图,只要ROI区域的长度和宽度确定,第一组静态路径实验的发射位置数量就是固定不变的;第三组是第二个移动信标的发射位置数量图,相对来说发射位置最少,效果最好。

图4 发射位置数量对比
图5 是3组实验中每个信标节点的移动路径对比图,从图中可知,第一组实验曲线的走势基本上与图4中的趋势一致。第三组实验也是第二个移动信标的路径长度,所以该信标的开销最小,效果也最好。
4 结束语

图5 路径长度对比
国内外学者对DV-Hop算法提出了许多的改进,大部分都是以降低三边测量或多边测量的误差为出发点,很少有人关注将定位误差和系统开销结合起来进行分析。本文不仅用群体智能算法对DV-Hop算法的定位误差进行改进,同时还用新的移动信标算法降低系统开销。从实验结果可见改进的DV-Hop算法提高了节点的定位精度,取得了较好的定位效果;提出的两个移动信标基于虚拟力的方法,效果比纯粹的静态路径或者动态路径具有更好的稳定性、灵活性和信号覆盖率,降低了系统开销。虽然增加的移动信标增加了少许系统成本,但换来的是系统定位质量的较大提高,因此具有一定的应用价值和较好的应用前景。
[1]Bartholdy Sanson J,Rodrigues Gomes N,Machado R,et al.Optimization of wireless sensor network using network coding algorithm[C]//Seville,Spain:The Twelfth International Conference on Networks,2013:21-24.
[2]ZHANG Xinping.A research on localization technique of wireless sensor networks[J].Guangzhou:South China University of Technology,2012(in Chinese).[张新平.无线传感器网络中的定位技术及应用研究[D].广州:华南理工大学,2012.]
[3]JIAO Binliang,ZHANG Ke.Localization algorithm based on stochastic proximity embedding in wireless sensor networks[J].Journal of Chinese Computer Systems,2013,34 (2):269-271(in Chinese).[焦斌亮,张可.基于SPE的无线传感器网络定位算法[J].小型微型计算机系统,2013,34(2):269-271.]
[4]Li Wenwen,Zhou Wuneng.Genetic algorithm-base localization algorithm for wireless sensor networks[C]//Seventh International Conference on Natural computation,2011:2096-2099.
[5]CHEN Xingzhou,LIAO Minghong,LIN Jianhua.Improvement of node localization in wireless sensor network based on particle swarm optimization[J].Journal of Computer Applications,2010,30 (7):1736-1738(in Chinese).[陈星舟,廖明宏,林建华.基于粒子群优化的无线传感器网络节点定位改进[J].计算机应用,2010,30 (7):1736-1738.]
[6]Zhao J,Fu Y,Wang H B.Localization technology based on quantum-behaved particle swarm optimization algorithm for wireless sensor network[J].Applied Mechanics and Materials,2012,220:1852-1856.
[7]Yu C B,Yu L,Tan J,et al.DV-Hop localization algorithm in wsn based on weighted of correction in hop distance[J].Applied Mechanics and Materials,2013,303:143-148.
[8]Luo X,Liu Y,Long C,et al.Range-free localization algorithms in wireless sensor networks[C]//Fifth International Conference on Machine Vision Algorithms,Pattern Recognition,and Basic Technologies,2013:42-49.
[9]FU Tao.Study on the hybrid localization algorithm of wireless sensor networks[D].Lanzhou:Lanzhou University,2012(in Chinese).[傅涛.无线传感器网络混合定位算法研究[D].兰州:兰州大学,2012.]
[10]SUN Jun,WU Xiaojun,FANG Wei,et al.Quantum-behaved particle swarm optimization:Theory and application[M].Beijing:Tsinghua University Press,2011 (in Chinese).[孙俊,吴小俊,方伟,等.量子行为粒子群优化:原理及其应用[M].北京:清华大学出版社,2011.]
[11]Zhou W,Shi W,Gao P,et al.Localization using a mobile beacon in wireless sensor networks[J].Information Technology Journal,2013 (12):323-330.
[12]LI Shijian,XU Congfu,YANG Yang,et al.Getting mobile beacon path for sensor localization[J].Journal of Software,2008,19 (2):455-467(in Chinese).[李石坚,徐从富,杨旸,等.面向传感器节点定位的移动信标路径获取[J].软件学报,2008,19 (2):455-467.]
[13]JIA Qingxuan,ZHANG Qianru,GAO Xin,et al.Dynamic obstacle avoidance algorithm for redundant robots with pre-selected minimum distance index[J].Robot,2013,35 (1):17-22(in Chinese).[贾庆轩,张倩茹,高欣,等.预选择最小距离指标的冗余机器人动态避障算法[J].机器人,2013,35 (1):17-22.]
