基于EMD和粒子群优化的LS-SVM的网络流量预测
2013-11-30朱倩雨覃锡忠贾振红
朱倩雨,覃锡忠,贾振红,盛 磊,陈 丽
(1.新疆大学 信息科学与工程学院,新疆 乌鲁木齐830046;2.中国移动通信集团新疆有限公司,新疆乌鲁木齐830063)
0 引 言
伴随着移动互联网、高清视频、在线游戏、云应用等业务的兴起,网络流量呈现爆炸式增长,电信运营商虽然不断地在提高网络带宽,却依然感受到 “带宽供不应求”的压力。对它的预测,为网络的流量控制、带宽分配、选路控制、故障管理等提供有效依据。这样,在网络过载发生之前,可以预先采取防范措施,来保证网络的正常服务。
现有的网络流量预测模型主要有时间序列模型、灰色模型、神经网络模型和支持向量机模型等,但这些模型在预测性能上都存在各自的缺陷,ARMA和ARIMA模型适应于线性预测,算法简单,易于实现,但预测精度不高[1]。灰色模型具有所需样本少,建模简单的特点,但对波动较大的数据预测精度低[2]。神经网络模型基于经验风险最小化原则,适应于非线性预测,但要求的训练样本多,存在局部最小、泛化能力弱等缺点,易造成预测精度不高[3]。基于网络流量数据的长相关、自相似、周期性、突发性和多尺度等特点,单一的预测模型已远远不能准确地刻画复杂性较高的流量变化的规律。
因此,许多专家学者充分利用各种单一预测模型的优点,对组合预测模型进行了探索和研究。大量实践研究结果表明,组合预测模型对复杂的流量特性的描述更加准确和全面,可以有效提高网络流量预测精度。而对于组合预测模型的研究大都建立在小波变换[4,5]的基础上,但在基于小波变换的预测中,存在确定分解层数以及小波基难以选择的问题[6]。EMD(经验模式分解)是一种新的信号处理方法,它能够吸取小波变换的多尺度分析能力的优势,从信号本身的尺度特征出发对信号进行分解,具有自适应性[7],属于自适应小波分解。SVM(支持向量机)基于结构风险最小化理论提出,具有结构简单、学习速度快、全局最优、泛化能力强的优点,能较好地解决数据的小样本、非线性、高维数等问题,预测能力较强[8]。优化的SVM泛化能力增强,更适合做长期预测[9]。根据网络流量序列的特点,结合EMD和SVM两种方法的不同功能,本文提出了基于EMD和粒子群优化的LS-SVM (最小二乘支持向量机)相结合的方法,对网络流量进行预测。对实际的网络流量数据进行仿真实验,证明了模型的有效性和可行性。
1 EMD和粒子群优化的LS-SVM的基本原理
1.1 EMD的基本原理
EMD算法消除以时间尺度为特征的自相似性,降低数据的复杂性,从而实现将非线性、非平稳数据的处理问题向线性、平稳的处理问题的转化,将原始信号分解为若干互不相关的本征模函数 (IMF),它们都具有原信号不同的局部特征信息,而且满足以下两个条件:① 函数在整个时间范围内,局部极值点数目和过零点数目必须相等或最多相差一个;②在任意时刻点,局部最大值的包络 (上包络线)和局部最小值的包络 (下包络线)平均必须为零[10]。
设任一信号为h(t),采用三次样条插值函数先对此信号的所有极大值拟合成上包络线,再对所有极小值拟合成下包络线[11],记两条包络线的均值为m(t),则可设一个新的信号为

当g(t)满足上述两个条件时,那么g(t)即为第一个IMF分量c1。设r(t)为信号余项,则

将r(t)视为新的原始信号,重复 (1)操作,可以依次得到第二个IMF分量c2,第三个IMF分量c3,…,第m个IMF分量cm,其中m∈N,是本征模函数的个数。此时最终的信号余项r(t)满足只有一个极值点或者单调函数的条件。于是信号可以表达为
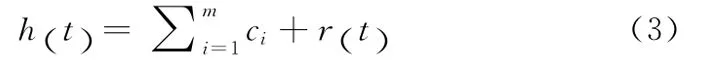
1.2 最小二乘支持向量回归机的原理
LS-SVM是利用二次损失函数,通过非线性映射φ(·),将低维非线性空间的数据转化为高维线性空间的数据,从而实现最小二乘支持向量机的回归问题。其原理如下[12]:
设n组用 于 训 练 的样本数 据 (xi,yi),i∈ (1,2,…,n),xi∈Rn是样本输入,yi∈R是样本输出,则其最优逼近回归函数可估计为

若满足结构风险最小化的条件

则求解目标方程可转化为

其中Υ为惩罚系数,w∈R为权向量,b为偏置,ei(i=0,1,2,…,N)为误差。
由以上式子可把目标优化问题转化为拉格朗日函数

其中αi为拉格朗日乘子。
定义核函数为K(xi,xj)=φ(xi)Tφ(xj),满足Mercer对称函数条件。核函数有多种形式,本文选用径向基函数 (RBF),其中σ是核函数宽度。于是可得非线性预测回归模型
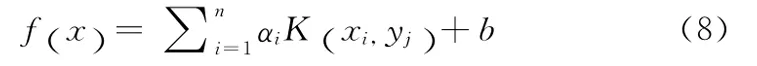
由于核函数和惩罚参数影响LS-SVM的预测精度,粒子群优化算法具有强大的全局搜索能力,实现起来较简单,故采用粒子群优化[13]算法来优化LS-SVM的参数,以获得较优的LS-SVM预测模型。
2 基于EMD和粒子群优化的LS-SVM预测模型
经验模式分解 (EMD)可以将非平稳的流量序列按其本身的尺度特征自适应地分解为若干不同尺度的平稳的IMF(固有模态)分量。根据各个IMF的特点,选择合适的LS-SVM模型对分解后的分量进行预测,最后通过SVM合成原始流量。模型的预测流程图如图1所示。
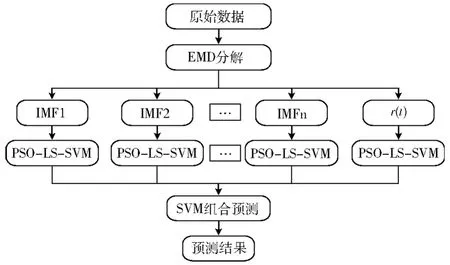
图1 EMD和粒子群优化的LS-SVM预测模型
其预测步骤为:
(1)EMD分解将流量序列进行EMD分解得到n个本征模函数和1个剩余分量。
(2)数据的处理由于流量数据的变化范围比较大,为了提高预测的精度,对分解后的数据进行归一化处理。
(3)LS-SVM模型的确定与训练对EMD分解后的各个IMF分量分别建立LS-SVM预测模型,模型的参数由粒子群优化算法得到。此模型采用多输入单输出[13]的预测方法,构造时间序列输入输出向量矩阵从而建立训练样本。训练样本结构如表1,其中x(i),x(i+1),x(i+2),x(k+i-1)作为输入向量,x(k+i)作为输出向量。k为输入向量的嵌入维数。
(4)LS-SVM模型的预测通过对每个分量训练可以确定粒子群优化LS-SVM[14]中的最优参数,从而建立预测模型,对测试集部分进行预测。
(5)流量的合成 由于分解后的每个IMF分量对最后的预测结果的贡献率不同,简单的线性相加将会影响模型最后的预测精度,故使用SVM来实现最优加权组合预测。先对每个预测值进行反归一化处理,再通过SVM对各个预测值组合得到最终的预测结果。

表1 构造时间序列输入输出向量矩阵
3 仿真实验
实验的数据来源于某电信公司CMNET网络的流量数据,采集了从2012年1月1号到1月25号共25天,每天每小时网络的访问量,得到600个数据。采用前400个数据作为训练样本,用于进行参数的估计及模型的确定,后200个数据作为测试样本,作为检测预测值和真实值差别的依据。取输入向量的嵌入维数为3,LS-SVM模型的参数由粒子群优化算法得到。本文采用均方误差 (mean squared error,MSE)作为评价预测结果的标准。图2为原始网络流量的数据。

图2 原始网络流量的数据
图3 为各个IMF分量真实值与预测值的差异。

图3 各个IMF分量及其预测值
从图3中可以看到,第一个分量IMF的预测效果不太理想,但是随着IMF频率的降低,预测精度逐渐提高。这种变化趋势可以从MSE误差上反映出来,见表2.

表2 各IMF分量预测的最小均方误差 (MSE)(%)
另一方面,也可由图3看出,预测误差较大的序列,较之误差较小的序列其幅值较小,所以当将各IMF预测序列合成后,大误差序列对预测结果影响不大,合成之后预测精度较高。将各个IMF预测序列用SVM合成,得到原始序列的预测曲线如图4所示。

图4 真实数据及其组合后的预测数据
为验证文中所提出模型的有效性和可行性,特采用单独的粒子群优化的LS-SVM和小波与粒子群优化的LSSVM模型作为对比模型,其预测曲线如图5所示。

图5 对比模型的预测曲线
从图5可以看出,采用EMD和PSO优化的LS-SVM组合模型后曲线的拟合程度优于其他两个模型,预测精度较高。这是因为原始非平稳的流量数据经过EMD自适应分解之后变成平稳的单一分量,并且这些分量具有一定的规律,跟原始的非线性、非平稳序列相比更易于预测。其预测误差比较见表3。

表3 各个模型预测的最小均方误差 (MSE)对比 (%)
4 结束语
根据网络流量时间序列所具有的特性,首先用EMD对信号做了平稳化处理。将具有复杂特性的原始流量分解为具有一定规律,相对比较单一,更加易于预测的时间序列。其次用粒子群优化的LS-SVM对各分量进行预测,最后通过SVM组合得到原始序列的预测结果。本文以真实的网络流量数据对算法进行了仿真实验,结果表明,该算法模型对网络流量的预测具有一定的优势,预测精度有明显提高,但在时间复杂度上有所欠缺,下一步的主要研究工作将在此方面展开。
[1]JIANG Ming,WU Chunming,HU Damin.Research on the comparison of time series models for network traffic prediction[J].Acta Electronica Sinica,2009,37 (11):2353-2359 (in Chinese).[姜明,吴春明,胡大民.网络流量预测中的时间序列模 型 比 较 研 究[J]. 电 子 学 报,2009,37 (11):2353-2359.]
[2]MA Hualin,LI Cuifeng,ZHANG Liyan.Network traffic prediction based on grey model and adaptive filter[J].Computer Engineering,2009,35 (1):155-157 (in Chinese).[马华林,李翠凤,张立燕.基于灰色模型和自适应过滤的网络流量预测[J].计算机工程,2009,35 (1):155-157.]
[3]Junsong W,Jiukun W,Maohu Z,et al.Prediction of internet traffic based on Elaman neural network[C]//Guilin:Chinese Control and Deeision Conference,2009:1248-1252.
[4]WEI Yongtao,WANG Jinkuan,WANG Cuirong,et al.Network traffic prediction algorithm based on wavelet transform and combinational models[J].Journal of Northeastern University(Natural Science),2011,32 (10):1382-1885 (in Chinese).[魏永涛,汪晋宽,王翠荣,等.基于小波变换与组合模型的网络流量预测算法[J].东北大学学报 (自然科学版),2011,32(10):1382-1885.]
[5]GONG Linming,ZHANG Zhenguo.Combination prediction model to network traffic based on grey-wavelet[J].Computer Engineering and Design,2010,31 (8):1660-1662 (in Chinese).[巩林明,张振国.基于灰色小波的网络流量组合预测模型[J].计算机工程与设计,2010,31 (8):1660-1662.]
[6]CHEN Xiantian,LIU Jingxian. Network traffic prediction based on wavelet transformation and FARIIMA[J].Journal of Communications,2011,32 (4):153-158 (in Chinese).[陈晓天,刘静娴.改进的基于小波变换和FARIMA模型的网络流量预测算法[J].通信学报,2011,32 (4):153-158.]
[7]WANG Jundong,QI Weigui.Prediction of river water turbidity based on EMD-SVM[J].Acta Electronica Sinica,2009,37(10):2129-2133 (in Chinese).[王军栋,齐维贵.基于EMDSVM的江水浊度预测方法研究[J].电子学报,2009,37(10):2129-2133.]
[8]HUANG Chenglung,WANG Chiehjen.A GA-based feature selection and parameters optimization for support vector machines[J].Expert Systems with Application,2006,31 (2):231-240.
[9]ZHOU Xiaolei,WANG Wanliang,CHEN Weijie.Network traffic prediction model based on wavelet transform and optimized support vector machine[J].Applications and Software of Computers,2011,28 (2):34-37 (in Chinese).[周晓蕾,王万良,陈伟杰.基于小波变换和优化的SVM的网络流量预测模型[J].计算机应用与软件,2011,28 (2):34-37.]
[10]Zhang X,Lai k K,Wang S Y.A new approach for crude oil price analysis based on empirical mode decomposition[J].Energy Economics,2008,30 (3):905-918.
[11]Balocchi R,Menicucci D,Varanini M.Empirical mode decomposition to approach the problem of detecting sources from a reduced number of mixtures[C]//Proceeding of the 25th Annual International Conference of the IEEE EMBS,2006.
[12]WU Haishan,CHANG Xiaoling.Power load forecasting with least squares support vector machines and chaos theory[C]//Proc of Intelligent Control and Automation,2006:4369-4373.
[13]WU Lianghai.Prediction of petroleum demand based on SVM optimized by PSO[J].Computer Simulation,2010,27 (4):291-295(in Chinese).[吴良海.基于粒子群优化支持向量机的石油需求预测[J].计算机仿真,2010,27 (4):291-295.]
[14]LIU Yuan,WANG Peng.Combining wavelet transform and Bayesian least squares support Vector machines to predict network traffic[J].Application Research of Computers,2009,26 (6):2229-2231 (in Chinese).[刘渊,王鹏.融合小波变换与贝叶斯LS-SVM的网络流量预测[J].计算机应用研究,2009,26 (6):2229-2231.]
