破碎与团聚对冰浆存储过程冰晶粒径演化的影响

徐爱祥，刘志强，王小倩，赵腾磊

(中南大学 能源科学与工程学院，湖南 长沙，410083)

冰浆(ice slurry)是指含有大量悬浮冰晶粒子的固液两相溶液，其具有较高的储能密度和良好的流动与换热特性而受到人们广泛关注[1−2]，并且在众多领域具有广阔的应用前景[3−4]。冰浆存储期间冰晶的数量和粒径存在着显著的变化，这些变化会对冰浆的流动与传热特性产生重要影响[5]。Kozawa等[6−7]从宏观角度研究了冰浆在存储槽内富集与分层现象，而这无法精确阐述冰浆存储中冰晶演化过程与机理。Pronk等[8]从微观角度出发，认为存储过程冰晶演化受磨损、团聚及Oswald熟化效应共同作用，而熟化效应的影响较为显著，但计算结果与实验存在较大差异。最近，Kumano[5]等分析发现团聚与破碎作用对冰晶粒径演化也有重要影响。上述研究表明，存储过程中冰晶演化的研究还不够全面，特别是微尺度下冰晶演化过程与机理还有待深入研究。群体平衡模型(population balance model,PBM)是描述离散体系中分散相实体尺度分布的有效方法[9]。PBM在化工领域的广泛应用[10−11]为冰浆存储过程离散相间相互作用的研究带来很大启示。冰浆系统是典型的离散系统，其基本特点是载流溶液携带大量的冰晶颗粒群。冰浆存储过程中冰晶生长与磨损、团聚与破碎等微观现象都是群体平衡方程(population balance equation, PBE)所要表达的内容。为此，本文作者针对冰浆存储过程离散特点建立冰晶颗粒群体平衡模型，通过Matlab自编程序，采用分区法对群体平衡方程进行离散求解，着重讨论破碎作用与团聚作用对冰晶粒径演化的影响。

1 冰晶群体平衡模型

1.1 数学建模

在建立冰浆存储过程冰晶粒径演化群体平衡数学模型时，进行如下假设：(1) 冰晶粒子在空间上均匀分布，且具有各向同一特性；(2) 存储过程冰晶的核化现象已不明显，过冷度随着冰晶的形成而逐渐变小，忽略冰晶的核化与生长；(3) 忽略外部空间对冰晶分布与演化的影响。因此，冰浆存储过程中冰晶粒径演化的零维空间群体平衡模型为

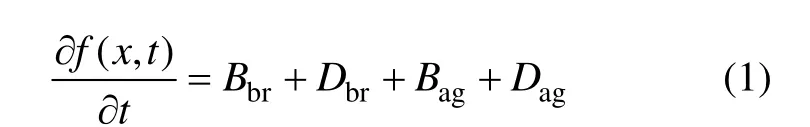
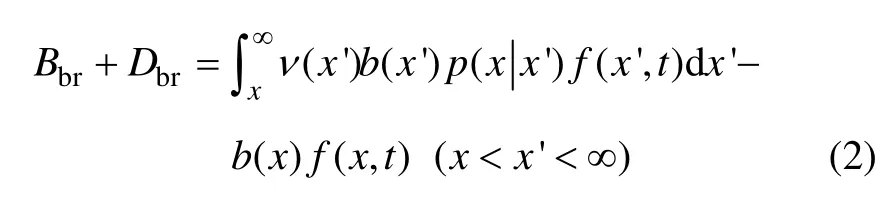
式中：Bbr为由于破碎动力学行为造成冰晶数值密度的增加量，表示粒径为x′的冰晶破碎成粒径为x子颗粒的生产率；Dbr为由于破碎动力学行为造成冰晶数值密度的减小量，表示冰晶破碎成子颗粒后粒径为x原颗粒的损失率；b(x)为破碎率(breakage frequency)，表示单位时间粒径为x的冰晶碰撞后发生破碎事件的速率；p(x|x′)为粒子概率密度函数(particle distribution function, PDF)，表示粒径为x′冰晶破碎后会形成粒径为x冰晶的概率；v(x′)为粒径为x′的冰晶破碎一次产生粒径为x冰晶粒子的平均个数，本文取v(x′)=2。

冰晶的团聚项为

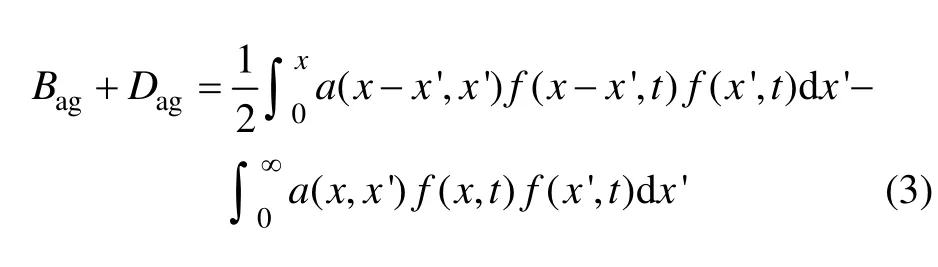
式中：Bag为由于团聚动力学行为造成冰晶数值密度的增加量，表示粒径为x−x′的冰晶与粒径为x′冰晶团聚形成粒径为x冰晶的生产率；Dag为由于团聚动力学行为造成冰晶数值密度的减小量，表示粒径为x的冰晶在参与下一次的团聚事件后会产生更大粒径的冰晶，从而造成粒径为x原颗粒的损失率；a(x,x′)为团聚率(aggregation frequency)，表示单位时间粒径为x与x′冰晶碰撞后发生团聚事件的速率。需要注意的是：式(2)与式(3)积分项的上限∞指的是在计算时冰晶粒子粒径的最大值。

根据模型假设，冰浆中冰晶粒子在惯性区域受流体扰动作用仍保持各向同性，故不同粒径的冰晶碰撞时破碎率[12]的表达式如下：

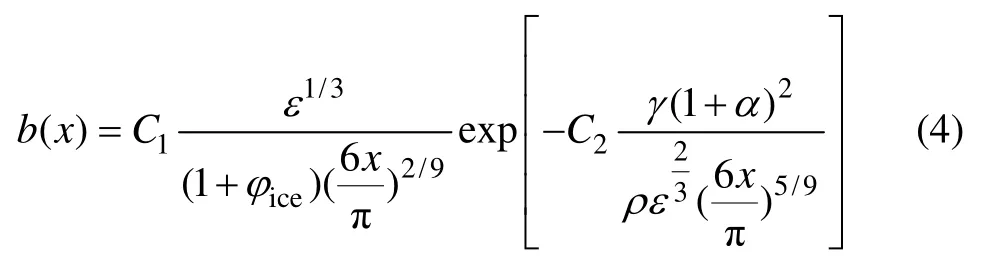
式中：ε为耗损率(dissipation rate)，表示单位质量的冰浆在外界扰动或内部粒子间相互作用下所耗散的功率，W/kg；γ为冰晶与载流溶液间的表面张力，mN/m；φice为含冰率，%；ρ为载流溶液的密度，kg/m3；C1与C2为破碎率中常数，其取值分别为0.004 81和0.08。

粒径为x′的冰晶破碎为粒径x的冰晶概率分布函数[13]为

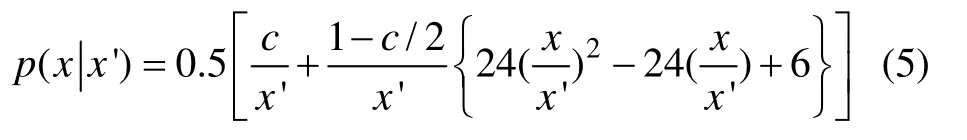
式中：c为形状因子，当冰晶为球形时，c可取为1。

根据上述假设，模型只考虑布朗碰撞作用下的团聚，因此，描述冰晶粒子在液相中的团聚率[12]为

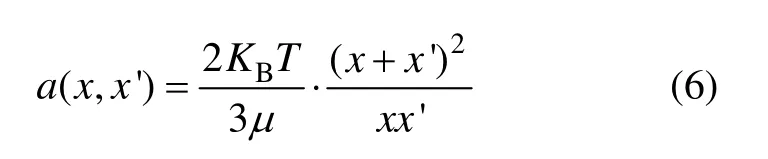
式中：KB为Boltzman常数，J/K；T为冰浆存储时的平衡温度，K；μ为冰浆中载流溶液的动力黏度，mPa·s。

模型中物性参数设置参照实验条件，计算所需要的各物性参数如表1所示[12]。实验中采用轻柔的搅拌方式以保持冰晶空间上的均匀分布，数值计算过程将其换算成耗损率。

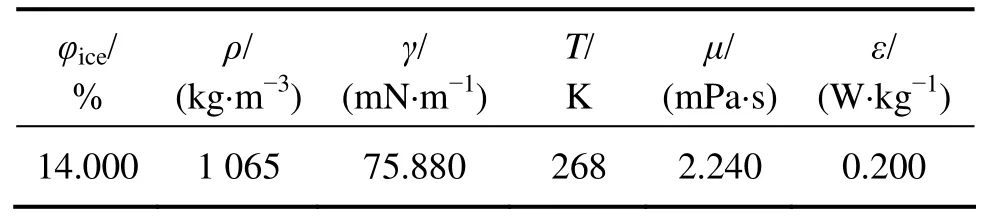
表1 载流溶液(9.2% NaCl)的物性参数Table 1 Physical parameters of ice slurry solutions(9.2% NaCl)

1.2 求解方法

群体平衡方程(PBE)是一个典型的混合积分与微分方程，其解呈非线性双曲形式，求解过程需采取特殊的处理方式以封闭方程。PBE的求解方法主要有以下3种[14]：(1) 分区法；(2) 矩法；(3) Monte Carlo法。其中，分区法的离散方式思路直观、简洁, 且能够得到颗粒尺度谱的动力学演变过程细节信息，计算精度与计算代价较适中。本文采用分区法对PBE进行离散求解：将冰晶尺度分布曲线进行离散，划分为有限数目个区间，在每个区间内针对某个冰晶粒径的分布函数，建立平衡方程，再联立求解这些平衡方程。需要指出的是：求解过程中利用基于核函数的积分中值定理封闭PBE右边的团聚与破碎项积分形式。上述求解过程通过Matlab自编程序来实现。

1.3 边界条件与初始条件

1.3.1 边界条件

在 0～10−11m 范围的冰晶粒径概率密度在方程中无法表达与计算，而据成核理论可知[15]，0～10−11m的冰晶粒子会有消融。因此，在任意时刻计算，可添加 1个与初始时刻相同的概率密度作为左边界条件，即。

1.3.2 初始条件

考虑实验中测定的初始状态冰晶粒径概率密度近似呈正态分布[16]，在数值计算中，初始条件参照实验结果中冰晶的初始分布形式设定，并通过实验结果拟合而得到，拟合关联式如下：

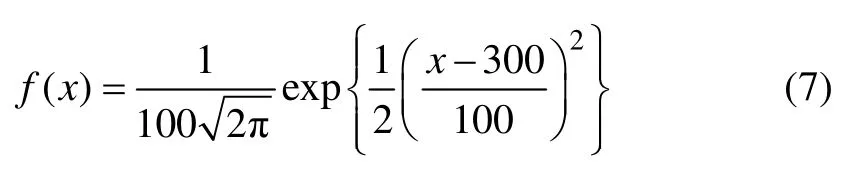
其中：x的取值范围为 10−11＜x＜vM+1。

2 模型验证

为验证本文建立的模型可靠性，将冰晶粒径概率密度及冰晶平均粒径的模拟结果与 Pronk的实验结果[17]进行对比，如图1和图2所示。从图1可以看出：冰晶粒径实验结果要比模拟结果稍偏高。从图2可以看出：冰浆存储22 h后，粒径分布实验结果与模拟结果在曲线谷峰有一定偏差，其余位置较吻合。实验结果与模拟结果存在一定的偏差，其主要原因是：(1) 由于实验过程中冰晶并非规则球状，所获取的冰晶图片也非规则的圆形，因此，冰晶粒径是经过专门的粒径图像处理而得到，而模拟中冰晶形状因子则按规则的球形来计算；(2) 冰浆实验存储过程可能涉及多种复杂微观过程，而模拟计算忽略了冰晶生长与磨损，这也会给计算结果带来偏差。通过定量比较，冰晶平均粒径的实验结果与模拟结果相对误差在 5%以内，冰浆存储22 h后冰晶粒径概率密度基本吻合，说明本文模型准确、可靠。

图1 存储期间冰晶平均粒径的变化Fig.1 Variations of average ice crystal size during storage

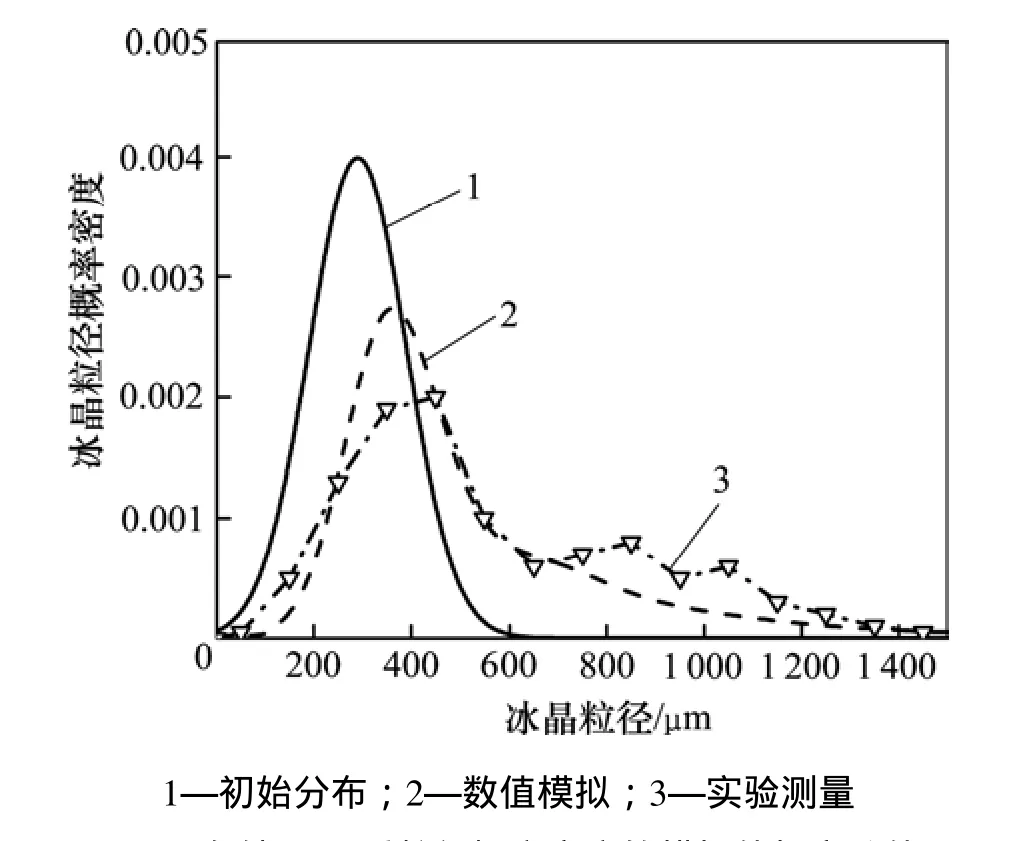
图2 存储22 h后粒径概率密度的模拟值与实验值Fig.2 Probability of ice crystal size distributions after 22 h storage obtained from model and experiment

3 模拟结果与分析

3.1 纯破碎作用

首先考察纯破碎工况下冰浆存储过程冰晶粒径分布与演化。图3所示为理想状态下冰晶碰撞只发生破碎现象时的粒径概率密度。由图3可知：随存储时间的推移，冰晶分布曲线整体有向左移动的趋势，也就是说，小粒径冰晶出现的概率增大，大粒径冰晶出现的概率减小；同时，峰值的左侧更远离初始分布，而峰值的右侧更靠近初始分布，这表明破碎作用对小粒径的冰晶影响更大，而对大粒径的影响较小。这主要是由于冰浆在存储过程中破碎作用使大粒径冰晶减少及颗粒冰晶不断增加。总体上，分布曲线移动幅度不大，且变化的幅度由快到慢，即在0～2 h内冰晶粒径有较小变化，2～22 h则无明显变化。这表明在存储过程中，破碎作用对冰晶的影响较小，且在短时间内，其作用有一定的影响；随着存储时间的增加，其作用逐渐削弱。

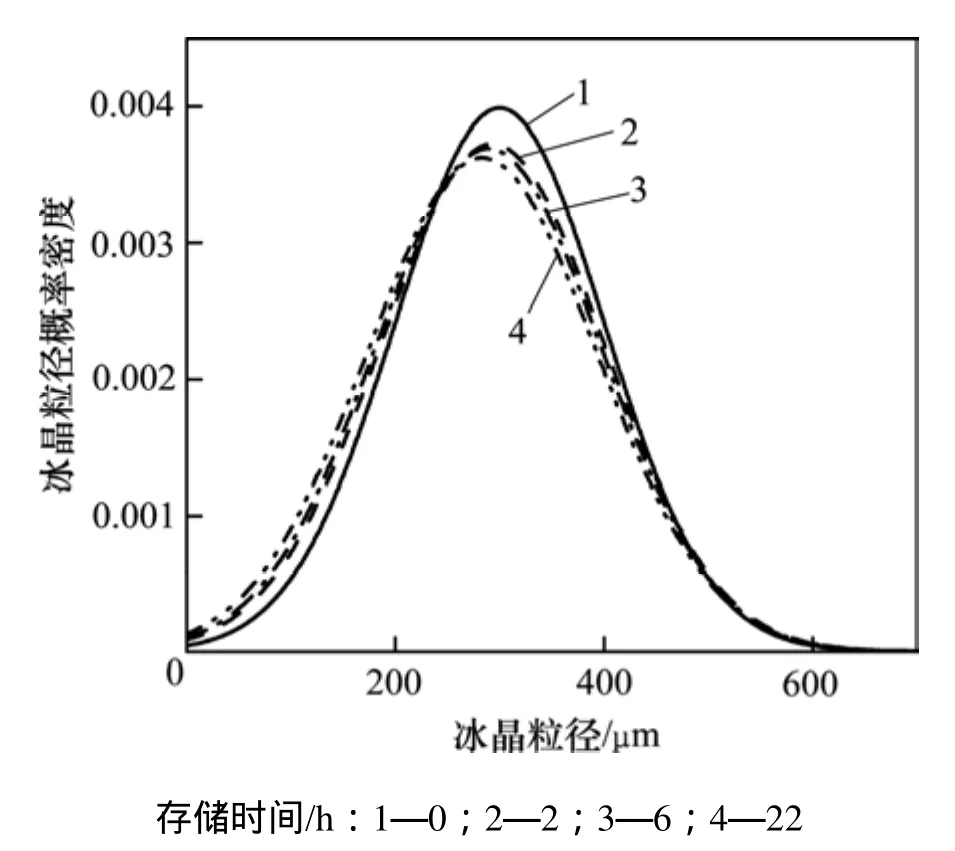
图3 冰晶在破碎作用下的粒径概率密度Fig.3 Probability of ice crystal size distributions in time under breakage

3.2 纯团聚作用

图4 所示为理想状态下冰晶碰撞只发生团聚现象时的粒径概率密度。由图4可知：与破碎作用下相反，随着存储时间的推移，团聚作用下冰晶分布曲线整体有向右移动，即小粒径冰晶出现的概率减少，大粒径冰晶出现概率增加；此外，峰值的左侧与右侧都远离初始分布，这表明团聚作用对所有粒径的冰晶都有影响。究其原因，主要是在存储过程冰晶粒子群在团聚作用下，颗粒与颗粒之间不断的黏附而导致冰晶整体呈现变大趋势。总体上来看，分布曲线移动明显，且变化的幅度由慢到快，即在0～2 h内冰晶粒径有较小变化，2～22 h则变化明显。这说明在存储过程中，团聚作用对冰晶的影响是显著的，且随着存储时间的增加，其作用也更加明显。

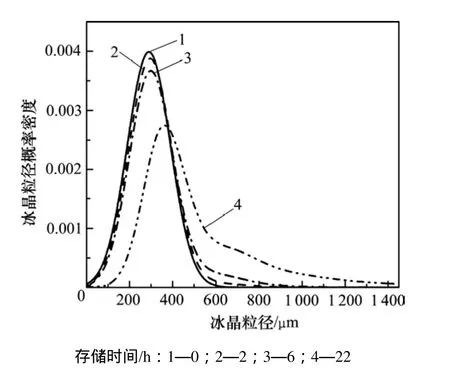
图4 冰晶在团聚作用下的粒径概率密度Fig.4 Probability of ice crystal size distributions in time under aggregation

3.3 破碎与团聚共同作用

在实际存储过程中，破碎作用与团聚作用同时发生，共同作用，因此，很有必要分析破碎与团聚共同作用工况下冰浆存储过程冰晶粒径分布与演化。图 5所示为冰晶在破碎与团聚共同作用下的粒径概率密度，如图5所示。从图5可见：随着冰浆存储过程的推进，冰晶粒径概率密度曲线向右移动且分布曲线坡度逐渐变缓，小粒径冰晶出现的概率减小，大粒径冰晶出现概率增大，随时间推移冰晶粒径分布范围变广。图6所示为共同作用下冰晶粒径分布函数。从图6可以看出：初始时刻冰晶粒径主要分布在100～500 μm，随着存储时间的增加，大粒径冰晶比例明显增加。对比纯破碎作用、纯团聚作用及破碎与团聚共同作用对粒径分布与演化的影响可看出：冰浆存储经历了破碎与团聚这2个不同作用的微观过程，2个“作用方向”相反，破碎作用下大粒径冰晶产生小粒径冰晶，而团聚作用下小粒径冰晶形成大粒径冰晶；此外，在存储初期，破碎与团聚单独作用下(见图3与图4)粒径概率密度曲线的变化比两者共同作用下(见图 5)粒径概率密度曲线的变化大，表明在共同作用时破碎与团聚对冰晶粒径的影响相互抵消；随着存储时间的增加，破碎作用不断削弱，而团聚作用依然明显，因此，二者的相互作用由最初的破碎与团聚“均衡作用”发展成团聚“主导”。这一现象的具体表现是冰晶在存储期间平均粒径会增大，图1证明了这一结论，冰晶的平均粒径从初始时刻的 300 μm 增长到存储 22 h后的392 μm。

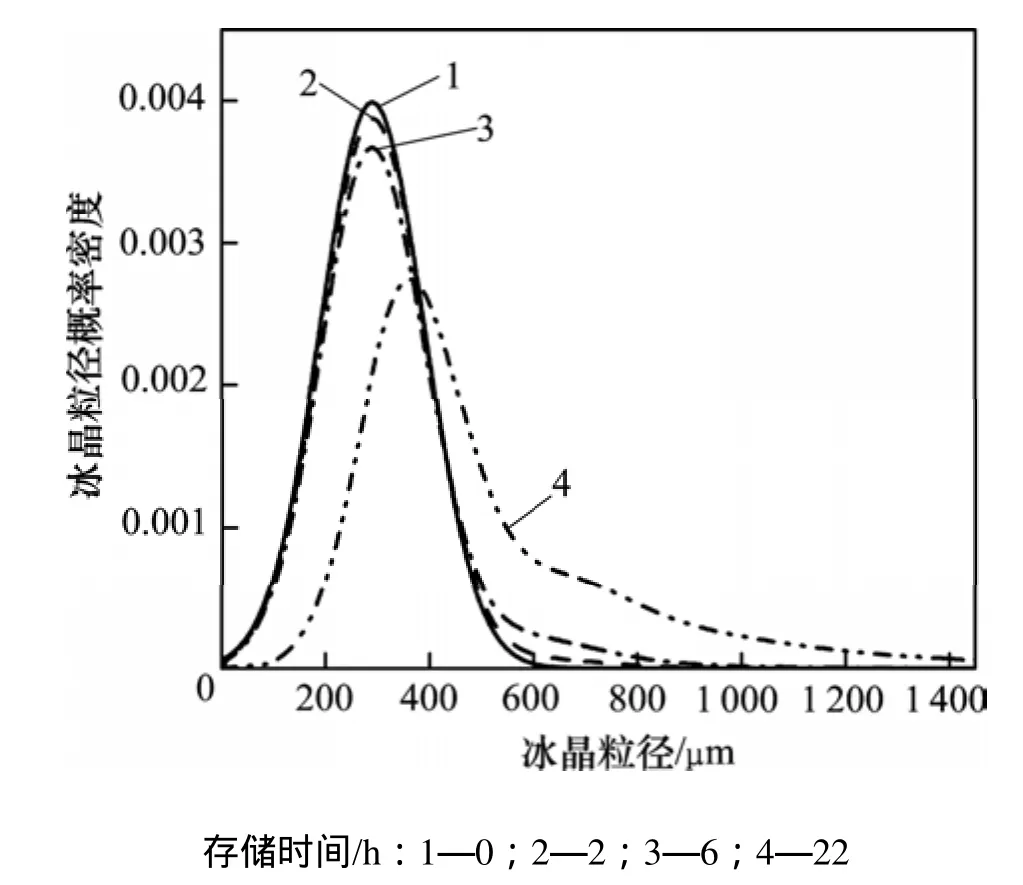
图5 冰晶在破碎与团聚共同作用下粒径概率密度Fig.5 Probability of ice crystal size distributions in time under breakage and aggregation

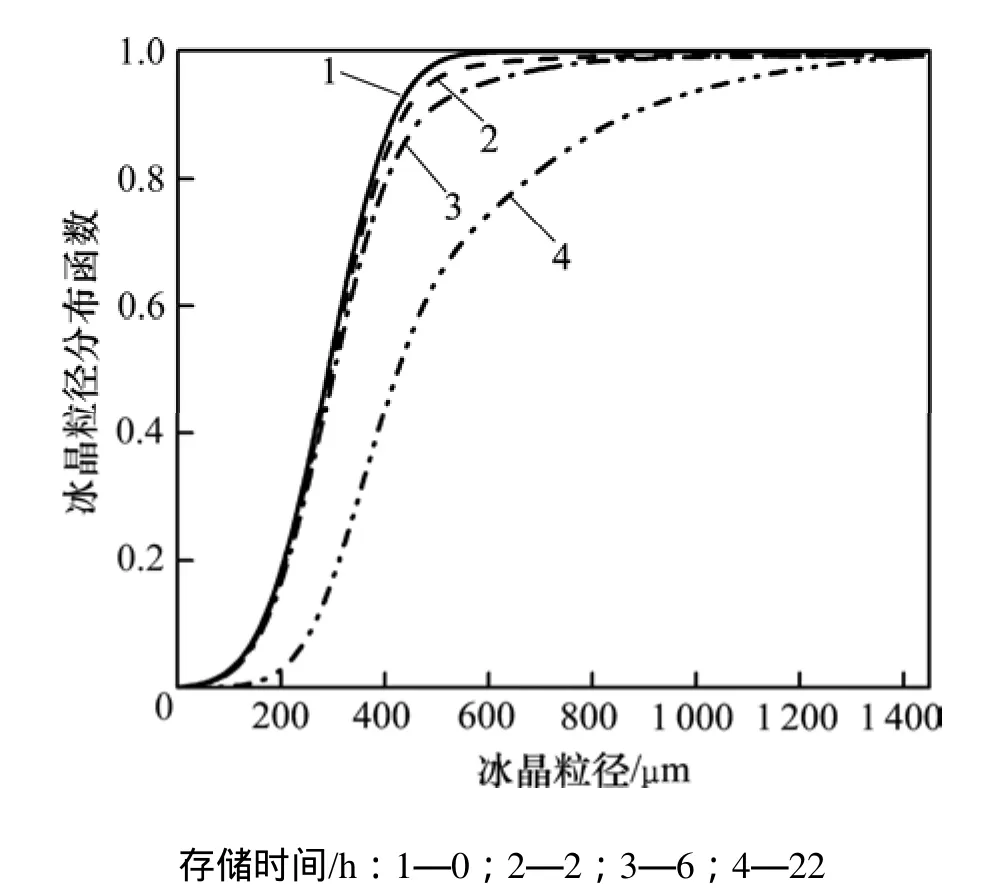
图6 冰晶在破碎与团聚共同作用下粒径分布函数Fig.6 Distribution function of ice crystal size distributions in time under breakage and aggregation

4 结论

(1) 引入群体平衡模型可较好地模拟冰浆存储过程的粒径分布及演化，获得了冰晶粒径概率密度随时间的变化关系：纯破碎作用下小粒径冰晶出现的概率增大，大粒径冰晶出现概率减小，纯团聚及两者共同作用下小粒径冰晶出现的概率减少，大粒径冰晶出现概率增加。

(2) 破碎与团聚是冰晶粒径演化的2个重要作用，在存储过程中，两者“作用方向”相反，且破碎与团聚经历从最初的破碎与团聚“均衡作用”发展成团聚“主导”的过程。

(3) 在冰晶存储过程中，冰晶平均粒径不断长大，即从初始时刻的300 μm增长到存储22 h后的392 μm，且模拟值与实验值相对误差在5%以内。

[1]Egolf P W, Kauffeld M. From physical properties of ice slurries to industrial ice slurry applications[J]. International Journal of Refrigeration, 2005, 28(1): 4−12.

[2]Ayel V, Lottin O, Peerhossaini H. Rheology, flow behaviour and heat transfer of ice slurries: a review of the state of the art[J].International Journal of Refrigeration, 2003, 26(1): 95−107.

[3]Kauffeld M, Wang M J, Goldstein V, et al. Ice slurry applications[J]. International Journal of Refrigeration, 2010,33(8): 1491−1505.

[4]Bellas I, Tassou S A. Present and future applications of ice slurries[J]. International Journal of Refrigeration, 2005, 28(1):115−121.

[5]Kumano H, Hirata T, Hagiwara Y, et al. Effects of storage on flow and heat transfer characteristics of ice slurry[J].International Journal of Refrigeration, 2012, 35(1): 122−129.

[6]Kozawa Y, Aizawa N, Tanino M. Study on ice storing characteristics in dynamic-type ice storage system by using supercooled water: Effects of the supplying conditions of ice-slurry at deployment to district heating and cooling system[J].International Journal of Refrigeration, 2005, 28(1): 73−82.

[7]青春耀, 肖睿, 宋文吉, 等. 冰浆在蓄冰槽内的蓄冰特性及其均匀度研究[J]. 低温与超导, 2009, 37(5): 41−46.QING Chunyao, XIAO Rui, SONG Wenji, et al. Study on ice slurry storing characteristics and its uniformity in ice storage tank[J]. Cryogenics and Superconductivity, 2009, 37(5): 41−46.

[8]Pronk P, Hansen T M, Ferreira C A I, et al. Time-dependent behavior of different ice slurries during storage[J]. International Journal of Refrigeration, 2005, 28(1): 27−36.

[9]Ramkrishna D. Population balances: Theory and applications to particulate systems in engineering[M]. San Diego: Academic Press, 2000: 30−45.

[10]顾兆林, 苏军伟, 李云, 等. 两相及多相体系的离散相行为与群体平衡模型[J]. 化学反应工程与工艺, 2007, 23(2): 162−167.GU Zhaolin, SU Junwei, LI Yun, et al. Behaviors of the dispersed phase in the multiphase system and population balance model[J]. Chemical Reaction Engineering and Technology, 2007,23(2): 162−167.

[11]Gerstlauer A, Motz S, Mitrovic A, et al. Development, analysis and validation of population models for continuous and batch crystallizers[J]. Chemical Engineering Science, 2002, 57(20):4311−4327.

[12]Marchisio D L, Vigil R D, Fox R O. Implementation of the quadrature method of moments in CFD codes for aggregation-breakage problems[J]. Chemical Engineering Science, 2003, 58(15): 3337−3351.

[13]Hill P J, Ng K M. New discretization procedure for the breakage equation[J]. AIChE Journal, 1995, 41(5): 1204−1216.

[14]赵海波, 郑楚光. 离散系统动力学演变过程的颗粒群平衡模拟[M]. 北京: 科学出版社, 2008: 70−79.ZHAO Haibo, ZHENG Chuguang. Population balance modeling for the process of the dynamic evolution in dispersed systems[M]. Beijing: Science Press, 2008: 70−79.

[15]Chégnimonhan V, Josset C, Peerhossaini H. Ice slurry crystallization based on kinetic phase-change modeling[J].International Journal of Refrigeration, 2010, 33(8): 1559−1568.

[16]Hansen T M, Radosevic M, Kauffeld M. Behaviour of ice slurry in thermal storage systems[R]. Atlanta: ASHRAE, 2002:93−107.

[17]Pronk P, Ferreira C A I, Witkamp G J. Effect of long-term ice slurry storage on crystal size distribution[C]// Melinder A.5th Workshop on Ice Slurries of the IIR. Stockholm: International Institute of Refrigeration, 2002: 151−160.