一种基于动态网格模板的DEM生成算法

潘雅辉，相方莉

(浙江长征职业技术学院，浙江杭州310023)

1 引言

建立高质量的数字高程模型(Digital Elevation Model，DEM)在土壤侵蚀研究、土地利用规划与评价、景观设计等领域具有重要意义［1-2］.目前，利用等高线生成DEM的方法较多，但在精度、效率等方面仍存在一些问题.如当等高线数据不足时，等高线直接内插法在确定内插所需要的参考点时会出现问题;变换函数法精度较低;趋势面分析法需要的样点数较多等.此外，上述DEM生成算法在计算机实现及集成方面也存在一定难度［3-6］.因此，本文设计开发了一种数字高程模型生成算法:动态网格模板法(DGT);并采用OpenGL图像库和组件技术，开发了一个三维可视化插件，实现了原始等高线数据、遥感数据及DEM数据的多源数据集成和一体化显示.

2 移动拟合法和加权平均法

DEM内插算法的实现是以待定点(未知高程值点)的周边相邻已知高程值的点为参考，求解待定点高程值的过程.任何内插算法都有一定的假设前提:原始地形的起伏变化是连续和平滑的;相邻点之间，无论是未知值的点还是已知值的点，它们之间都有很大的关联性或相关性，只有这样才有可能通过相邻的已知值的点来求解出或内插出待定点的高程值.本文所采用的DGT算法属于逐点内插.

2.1 移动拟合法

在移动拟合法中，一般可以选取与待定点邻近的、高程值已知的数据点作为参考点，来拟合一个多项式曲面，曲面拟合公式如下:

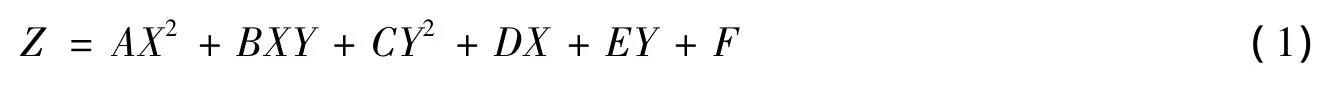
式中 X、Y、Z 是各参考点的坐标值，A、B、C、D、E、F 为待求解的参数［7］134.移动拟合法主要涉及以下两方面的问题:(1)如果参考点太多，会影响计算效率;而太少，则会影响计算精度甚至根本无法求解.为了保证有充足的参考点，就必须确定合理的最小邻域.(2)参考点距离待定点有近有远，与待定点的相关性会有所不同，因此确定各参考点的权重也很重要.

最小邻域的确定有搜索范围和参考点数量两个影响因素.图1为基于范围选点的例子，其选中的点(参考点)都位于以待定点为圆心、R为半径的圆形范围之内.R值的大小取决于原始数据点密度情况和可能影响的范围.根据二次曲面方程求解的需要，同时保证插值的效率，可采用动态搜索圆解决这个问题，即根据数据点平均密度确定圆内数据点(平均要有10个)，从而求得搜索圆的半径，其公式如下:

式中N为总点数，A为总面积.

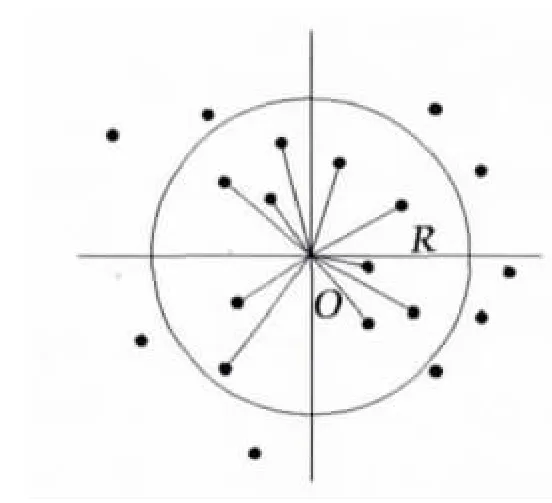
图1 基于范围选参考点

2.2 加权平均法

移动拟合法需要求解复杂的误差方程，为了运算简便快捷可将加权平均法看作移动拟合法的特例，其参考点范围的确定与移动拟合法相同［7］136.求解待定点x的高程值的公式如下:

式中Zi是第i个参考点的高程值，n为参考点数量，xi是第i个参考点的权重，Zx是待定点x的高程值.对于权重的确定，一般采取与距离相关的权函数，常用的权函数有:

式中R是搜索圆的半径，r是待定点到参考点的距离，p是参考点的权重.

3 DGT算法设计

3.1 DEM 建立流程

在本研究中，等高线生成DEM模型的基本步骤为:(1)将地形图中的等高线要素层数字化生成含高程属性值的ESRI Shape file文件格式.(2)确定X、Y方向的网格数，并生成网格矩阵.在本算法中，网格不一定是规则正方形，X值和Y值可以不同.确定X、Y方向网格数量的公式为:X方向网格数量 =等高线要素层X方向空间范围/网格X方向宽度;Y方向网格数量 =等高线要素层Y方向空间范围/网格Y方向宽度.(3)初始化参考网格值，即给参考点赋初始值.(4)根据已赋值网格点内插出未知高程的网格点的高程值.

3.2 等高线栅格化

等高线栅格化是指构建一个N*M的网格矩阵，并初始化每个网格的高程值.具体步骤如下:(1)为每个网格赋以－999999的初始高程值.若某网格高程值为－999999，则表示该网格高程值还未求解.(2)遍历每个网格，判断是否有等高线经过网格，如有1条等高线经过，则采用直线内插算法把等高线高程值赋给该网格;若大于1条等高线经过网格，则取距离加权平均值，距离值以等高线到网格中心的垂直距离计算.(3)对无等高线经过的网格，如图2(a)中的g1和g2网格，栅格化后的高程值仍为－999999，图2(b)中如黑色网格所示.对于这些未获取高程值的网格，将采用DGT算法通过内插计算得到高程值.

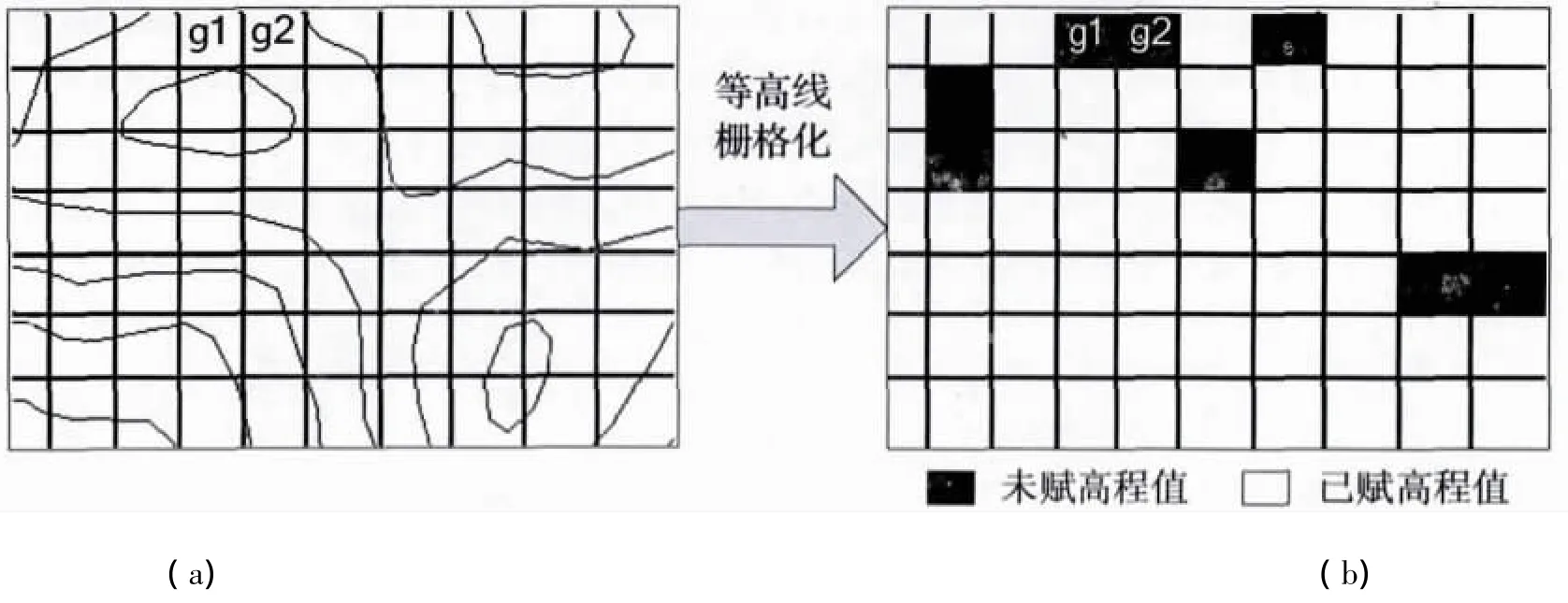
图2 等高线栅格化

3.3 未知高程网格内插

DGT算法的核心是确定动态网格模板，选择合适的权函数与插值函数来计算待定点高程值.

3.3.1 参考网格数量的确定

相对于政府一元独大的管理模式，多元主体合作共治的最大特点，在于它可以把多元主体置于社会治理系统之中，实现多元主体的优势互补，克服多元主体各自的局限，实现社会治理系统的整体优化。而从新时代构建共建共治共享格局的要求讲，它可以解决社会治理领域社会组织和公众参与发展不平衡、不充分问题，最大限度地激发社会组织活力和公众参与热情，促进社会进步，减少社会治理成本。

参考网格的数量通常是取4或8个，经过对内插效果的反复测试对比分析，DGT算法默认取8个参考网格进行计算.

3.3.2 插值函数与权函数的确定

DGT算法中插值函数采用式(3)，权函数采用与距离相关的权函数:

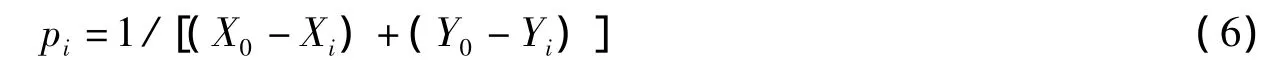
式中pi是参考点i的权，(X0，Y0)是待定点的X坐标和Y坐标，(Xi，Yi)是参考点i的X坐标和Y坐标.

3.3.3 确定动态网格模板

DGT算法中，动态网格模板需在一开始确定.图3为一个5×5的模板，黑色网格为待插值网格，其值通过搜索周围的24个网格内插计算而得(其中可能含有待插值网格).为了避免所选取的数据点集中在某个方向而造成参考点分布不均，DGT算法以待插网格为中心，将5×5平面分为1、2、3、4四个区，每个区有6个网格.内插计算时，DGT算法将从每个区取2个已知高程的网格作加权平均，这就克服了传统移动拟和数据点偏向的缺点.模板矩阵的大小是通过区的大小确定的.图4中区的大小是3×2，即Matrix(区的长轴)=3，所以模板的大小是5×5.如果区的大小是4×3，则模板大小是7×7，依此类推.

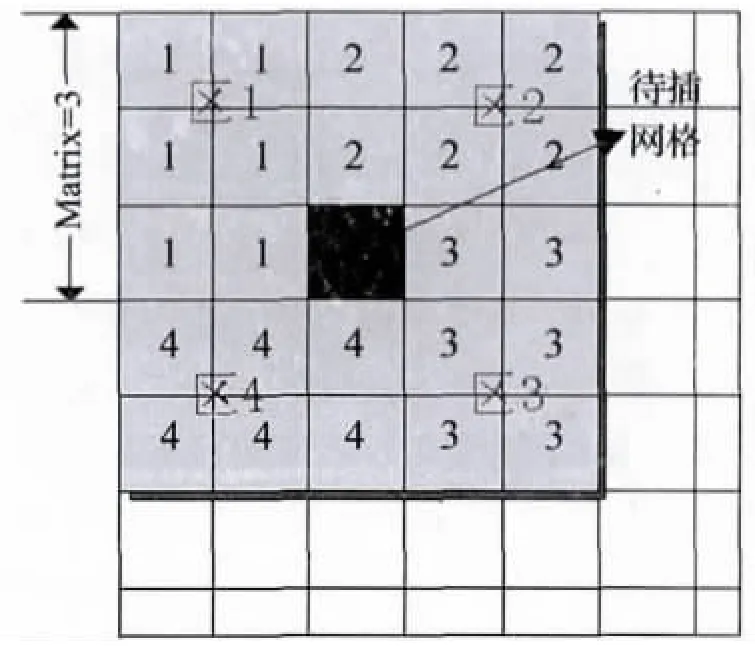
图3 动态网格模板

3.3.4 参考网格的搜索

在求解网格的高程值前，需要搜索到8个参考点.DGT算法首先从待插网格周围的(Matrix-1)圈的网格开始搜索，搜索的顺序是:区1，区2，区3，区4.每个区的搜索方式相同，其流程如图4所示.DGT算法在每个区取两个已知高程值的网格作加权平均，若在某个区域搜索不到2个已知高程值的网格做参考点，则模板在该区向外扩张1个网格，即在第Matrix++圈的网格中搜索参考点，直到取到2个已知高程值的参考点为止.当搜索超界即超出数据边界时，若仍未找到2个参考点，结束搜索.

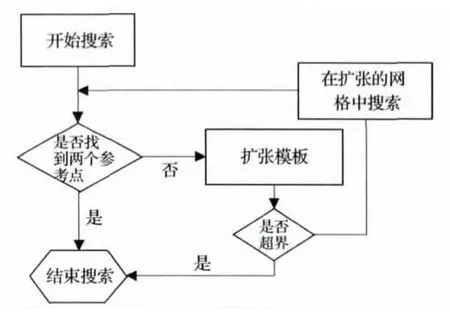
图4 参考网格的搜索

4 程序实现

4.1 DEM 数据结构

dtmDX:X方向的网格数

dtmDY:Y方向的网格数

minDGXx:高程模型原点即左下角X坐标

minDGXy:高程模型原点即左下角Y坐标

CellSize:格网间距值

NODATA_value:格网没有数值时的标记，用－999999表示

……

4.2 测试效果

为了能更直观地显示插值效果，本研究基于OpenGL图形库开发了一个三维可视化组件，将DGT算法采用C++语言进行程序实现后，集成到该三维可视化组件中.此处选择浙江省安溪流域1:10000比例尺地形图12幅，经扫描跟踪数字化生成Shapefile文件格式的等高线数据.图5中等高线数据经DGT算法内插，生成ARC/INFO ASCII GRID格式的DEM数据，经简单着色处理，以栅格图像方式显示如图6所示.图7为DEM数据在三维可视化组件中以网格方式显示的三维效果.

5 结语

DGT算法采用动态网格模板的方式进行参考点搜索，不用进行离散点值的求解，也不用采用搜索圆来搜索内插所需要的参考点，提高了插值的运算效率.该算法已被成功运用于安溪流域，测试结果显示:对于较为连续和平滑的地形，DGT算法计算效率较为理想;但对于尖锐变化或极不规则的地形区域，该算法会出现数据平滑性“低频滤波”现象，有待以后不断改进和完善.

［1］叶爱中，夏军，王纲胜，等.基于数字高程模型的河网提取及子流域生成［J］.水利学报，2005，36(5):531-537.

［2］张彩霞，杨勤科，段建军.高分辨率数字高程模型的构建方法［J］.水利学报，2006，37(8):1009-1014.

［3］王家耀.空间信息系统原理［M］.北京:科学出版社，2001:158-160

［4］张超.地理信息系统实习教程［M］.北京:高等教育出版社，2000:190-193

［5］邱卫宁.根据等高线建立数字高程模型［J］.武汉测绘科技大学学报，1994，19(3):199-203.

［6］余鹏，刘丽芳.利用地形图生产DEM数据的研究［J］.测绘通报，1998(10):16-18.

［7］李志林，朱庆.数字高程模型［M］.武汉:武汉大学出版社，2001.