基于突变理论的列车脱轨机理研究
2013-11-27李竹文戴焕云
李竹文,戴焕云
(西南交通大学牵引动力国家重点实验室,四川成都 610031)
有关列车脱轨的理论与试验研究成果丰硕[1],最早研究脱轨问题的法国科学家Nadal根据车轮出现爬轨趋势的静力平衡条件,定义了车轮爬轨所需的最小脱轨系数,即著名的 Nadal公式[2]。尽管 Nadal准则一直被广泛采用,但它较保守,求得的脱轨系数不能很好地反映车轮脱轨的安全性[3-5]。试验中发现,即使运行车辆脱轨系数大大超过了Nadal脱轨评判标准,但车辆也未出现明显的脱轨现象;而对脱轨事故的调查中,发现脱轨车辆和事故发生地点的线路状态往往符合现有安全标准。
脱轨系数的推导是基于单轮对准静态条件,这与当今车辆的实际运行状况有很大差别。高速车辆轮轨间的动态作用效应较强,难以仅用一个简单的脱轨系数来揭示动态脱轨机理。由于轮轨关系非常复杂,影响脱轨的因素较多,至今人们对脱轨的机理并未完全掌握。因此,有必要对现行的脱轨评判标准和方法重新认识和分析,寻求更为合理和直观的评判方法。突变理论为脱轨理论的研究提供了新思路,本文应用突变理论中的突变模型,综合考虑影响列车脱轨的几个因素,建立列车脱轨突变模型对脱轨问题进行分析。
1 突变理论简介
突变理论(Catastrophe Theory)是法国数学家Thom于20世纪70年代提出的一种拓扑学理论[6],用于研究动态系统在连续发展过程中出现突然变化的现象,解释突然变化与连续变化因素之间的关系,能直接处理不连续性的问题,适用于内部作用机理未知系统的研究。它以拓扑学、奇点理论和结构稳定性理论等数学理论为主要工具,建立突变模型,描述现实世界某些事物形态、结构突然变化的规律。突变理论认为突变与渐变的本质区别是系统势函数在临界点的附近有无“不连续”,通过分析分叉集的性质来实现对突变现象的界定与控制[7-8]。Thom在突变理论中研究了初等函数的分类问题,通过建立微分方程与函数之间的联系,对梯度系统中的奇点进行了分类。在最近几十年学者不仅将突变理论应用于数学、力学和物理等自然科学领域中,还将它应用于医学、生物学、经济学、社会科学以及人文科学等领域,均取得了丰硕成果[9-11]。
随着科学技术的发展,系统规模的扩大、数目的增多造成了系统之间的关系复杂化,因此对系统之间关系的研究也变得越来越困难。突变理论在解决类似的问题时具有一定的优势。根据突变理论的研究对象、发展历史及其应用领域来看,突变理论在非线性科学中是一种很有用的数学工具。
1.1 突变特征
突变现象通常有几个基本的特征:①多模态。系统状态空间中可能出现两个或多个稳定状态,因而在改变参数时,系统才可能发生突变。②不可达性。在不同稳定状态中存在着不稳定的状态,系统从一个稳态向另一个稳态跃迁的过程中直接跨过了这个态,不稳定的状态在实际中是不可达的。③发散。控制参数数值的有限变化会导致状态变量平衡位置数值的有限变化。不同控制参数的取值使系统发生变化,而从一个稳态向另一个稳态的转变是突然完成的。通常,控制参数数值的一个小摄动只引起状态变量的初值和终值的微小变化,但在退化临界点附近,控制参数初值的微小变化却可能导致状态变量终值的很大变化。物理过程的这种对控制参数路径摄动的不稳定性称为发散。④突跳。系统的突跳性是最常观察到也是最容易使人想到的可以应用突变理论的突变指征。突跳意味着系统势能在很短时间内有一个很大的改变。⑤滞后。突变的发生与控制变量变化的方向有关,控制变量从一个方向变化和控制变量从另外一个方向变化发生突变的状态是不相同的,有滞后现象。在分岔曲线附近,控制参量变化路径的微小不同会引起系统产生完全不相同的状态。
1.2 突变模型
系统中出现两个以上突变特征时,可以考虑采用突变模型对系统进行分析,通过选取状态变量和控制变量,建立突变模型对问题进行求解。具体的突变模型及使用参数如下:
1)折叠突变系统模型
势函数V(x)=x3+ux,1个状态变量x,1个控制变量u,突变流形
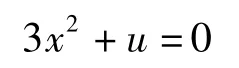
2)尖点突变系统模型
V(x)=x4+ux2+vx,1个状态变量,2个控制变量u,v,突变流形

3)燕尾突变系统模型
V(x)=x5+ux3+vx2+wx,1个状态变量,3个控制变量 u,v,w,突变流形

4)蝴蝶突变系统模型
V(x)=x6+tx4+ux3+vx2+wx,1 个状态变量,4个控制变量 t,u,v,w,突变流形

5)双曲脐点突变模型
V(x,y)=x3+y3+wxy-ux-vy,2个状态变量 x和y,3个控制变量,突变流形

6)椭圆脐点突变模型
V(x,y)=(1/3)x3- x2y+w(x2+y2)- ux+vy,2个状态变量,3个控制变量,突变流形

7)抛物脐点突变模型
V(x,y)=y4+x2y+wx2+ty2-ux-vy,2个状态变量,4个控制变量,突变流形
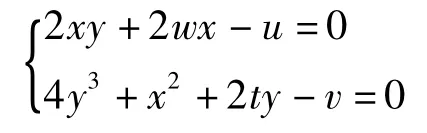
式中,V(x)表示一个系统的状态变量x和y的势函数,状态变量的系数u、v、w、t表示该状态变量的控制变量(更复杂的系统一般不适用此方法)。
2 列车脱轨突变模型
动态系统的势函数表示系统具有某种趋向的能力,可以描述为V=V(x,c),其中x为系统状态变量(系统输出变量),c为系统控制变量(系统外部输入变量)。当势函数一阶导数为0,其 Hessen矩阵不等于0时的点称为孤立临界点(Morse点),系统的状态呈连续光滑的变化;当势函数一阶导数及Hessen矩阵均为0时的点称为非孤立临界点(非Morse点),系统的状态可能发生突变。因此突变理论的关键便是寻求非孤立临界点构成的集合(分叉集),对其进行分析以揭示系统突变的形式及发生的机制。
列车运行过程中脱轨是一个复杂的变化过程。按照系统论观点,一方面,列车在轨道运行过程中持续受到脱轨系数和冲角两个因素的共同作用,这两个要素和列车运行状态一起组成了一个动态系统;另一方面,列车脱轨是一个连续性与突变性相统一的发展过程。连续性指系统内部“列车运行状态—脱轨系数—冲角”各要素的不安全状态变化是一个连续积累渐变的过程,具有一定的规律性;而导致的结果(列车脱轨)却是直接由安全状态到危险状态的不连续突变结果。由此可见,列车脱轨的发生可以理解为系统内部参数脱轨系数和冲角(控制参数)的连续变化引起系统状态的突然质变,系统从安全运行状态转化为脱轨状态实际上是一种突变现象。因此,将突变理论应用于列车脱轨成因机理分析中,建立列车脱轨突变模型来解释和描述列车脱轨的发生过程是可行和必要的。
2.1 列车脱轨尖点突变模型的建立
基于以上分析,列车在运行过程中主要受到脱轨系数与冲角的共同作用,此时列车的运行状态是非控制的。列车脱轨势函数V=V(x,c),其中V表示列车运行系统保持稳定运行趋势的能力;x表示列车运行系统安全状态变量,表示系统总体是否安全,为一维变量;c表示影响列车运行系统安全状态变化的控制变量即前面提到的列车脱轨系数和冲角,为二维变量。因此列车脱轨事故系统是通过二维控制变量(脱轨系数和冲角)以及一维状态变量(列车运行系统安全状态)来共同反映列车运行系统的势能。根据前文中提到的各突变模型的维数分析,应选用尖点突变模型对列车脱轨事故进行模拟。在用突变控制理论研究列车在轨道运行状态时,脱轨系数与冲角为控制变量,分别设为u和v,已知列车运行状态x为状态变量,则列车在运行中的突变特性可以通过尖点突变模型来描述,尖点突变模型的势函数为
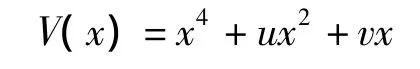
状态空间是三维的(x,u,v),状态变量为 x,控制变量有两个,即u和v。由势函数对状态变量求导得平衡曲面M的方程

它在三维空间(x,u,v)中的图形称为突变流形,这是一个有褶皱的曲面,列车运行系统的所有临界点都在该曲面上,而在不同的区域内平衡位置也是不同的。系统的安全状态变量x受到控制变量u和v的约束,随控制变量的变化而变化。在突变理论中,当系统处于稳定状态时,安全状态变量取得唯一极值,此时对应于上下叶的平衡位置是稳定的;当系统的安全状态变量x多于一个极值时,系统就处于不稳定的状态,此时对应于中叶的势函数取得最大值。
对平衡曲面方程M求导,得到的非孤立奇点集S满足方程
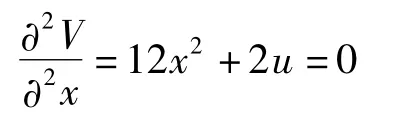
且是平衡曲面M的一个子集。
联立

消去 x,得

此式即为分叉集B,是奇点集S在控制平面u—v上的投影。由于分叉集是同时满足平衡曲面方程和平衡曲面对状态变量的导数方程,故分叉集在控制平面上的表达式为

写成分解的形式为

把列车运行状态系统的平衡曲面M和分叉集B绘制出来,得到列车脱轨尖点突变模型,如图1所示。

图1 列车脱轨尖点突变模型
2.2 突变分析
综上所述,列车运行过程中在脱轨系数和冲角作用下的突变机制可以通过尖点突变模型图进行定性描述。列车运行的状态由坐标空间中的点表示,故相点必在平衡曲面上。图1中的曲面表示列车运行过程中系统平衡曲面,底平面是脱轨系数和冲角两个控制变量所在的平面,控制平面上的曲线即为分叉集。平衡曲面的上下两叶是稳定结构,中叶是不稳定的。平衡曲面的上叶代表列车运行过程中在受脱轨系数和冲角作用前的稳定状态;中叶带有褶皱部分为不可达区域,为一对多区域,表示系统发生突变现象,即发生列车脱轨;下叶代表列车运行过程中在受脱轨系数和冲角作用后姿态发生突变脱轨后的另一稳定状态。中叶褶皱投影到底面控制平面,便得到分叉集,它形象地表明列车脱轨的发生条件,即当列车运行系统中的两控制变量(脱轨系数和冲角)落入分叉集时,系统状态变量x突变引发列车脱轨。所以稳定的列车运行状态应在曲面上叶或在曲面的下叶上,中叶对应于不稳定状态,也就是列车运行状态发生突变的那一刻的状态。
当控制轨迹越过分叉点集,若相点恰好在曲面终止的边缘上(曲面回折形成的中叶处),则它必定跳跃到另一叶上,这样就导致了列车运行状态x的突变。也就是当点P在控制空间上移动时,势函数V(x)值为最小值,对应于状态的稳定平衡;当P在尖点范围(分叉集B)里时,势函数V(x)有两个极小值,它们互相牵引,由Maxwell约定,系统总是转移到使它的势全局极小的稳定平衡位置。故在此不稳定状态下,列车运行状态变量x不是跳回到平衡曲面上叶就是跳到平衡曲面的下叶,最终导致了系统状态的突变。
将分叉集分为两部分,如图2所示。左半部分为列车由稳定运行状态向脱轨状态变化,右半部分为列车由突跳状态向稳定运行状态变化。列车脱轨突变从起动到发展的过程就是从上叶到下叶跃迁的过程。图2中分叉集的阴影部分为引发突变发生列车脱轨的危险区域。脱轨系数和冲角为控制变量,它们的运动轨迹在控制空间内,为一个平面。随着控制变量u和v的变化,(u,v)点划出一条控制轨迹。同时,相点沿着控制轨迹上方的平衡曲面上的一条轨迹移动。u和v的平稳变化几乎总引起x的平稳变化。

图2 分叉集
由图2可以得到:随着冲角的增大,危险区域变大,脱轨的危险性增大;对应一个较小的脱轨系数值,在冲角很大时,脱轨的危险性依然存在;在冲角很小时,危险区域边界对应的脱轨系数比冲角大时对应的脱轨系数值要大;减小冲角,从而减小危险区域,有利于防止列车脱轨。
分叉集右半部分表示列车运行状态变量x跳回到平衡曲面的上叶,即为列车跳起轨道运行一段时间后没有脱轨,而是车轮掉落回轨道,重新继续稳定运行,也就是说列车在脱轨系数和冲角作用下回到了初始的稳定状态,称此突变为有益突变,即列车在运行过程中经受住了脱轨系数和冲角的共同作用而运行状态未发生变化。这样就解释了在调查列车脱轨时发现列车在轨道上表面运行一小段距离又掉落回轨道的现象。
3 实例仿真分析
本文选用某型列车应用Simpack动力学软件进行多体系统建模,应用突变理论分析列车脱轨现象。考虑车体质量、构架和轮对的质量、转动惯量、质心几何位置、悬挂参数等,建立车辆系统动力学仿真模型。对该模型在一定的运行速度工况下施加轨道激励谱后,分别对其脱轨系数、冲角等特性分3种工况进行计算。工况一、二、三对应速度等级分别为150,200和250 km/h。各工况脱轨系数时间历程和冲角时间历程见图3~图5。
对图3~图5在不同的速度级别下运行的脱轨系数值和冲角进行分析,得到脱轨系数随冲角的变化分布情况,见图6~图8。

图3 工况一

图4 工况二

图5 工况三

图6 工况一

图7 工况二

图8 工况三
由图6~图8可得:对应于不同速度等级,脱轨危险区域主要集中分布在正冲角部分,负冲角有利于防止脱轨;对于较小的冲角,脱轨系数超过临界脱轨系数标准时列车脱轨危险性不大;对于较大的冲角,虽然脱轨系数未超过脱轨系数临界值,列车脱轨危险性却很大。在相同脱轨系数下,减小冲角有利于防止脱轨。
4 结语
本文利用突变理论中的尖点突变模型,以脱轨系数和冲角为控制变量,建立列车脱轨突变模型,研究列车在行驶过程中受到控制变量作用运行状态发生突变的情形。通过建立车辆动力学模型,分析了在不同速度下列车脱轨系数和冲角的分布,以验证突变分析结果。
本文所建立的列车脱轨突变模型,是列车脱轨机理研究的一种新方法,同时也将突变理论开拓性地应用到列车脱轨分析中,提出一种全新的列车脱轨解释。由于轮轨问题的复杂性,影响列车脱轨的因素众多,列车脱轨突变过程十分复杂,建立更为具体的列车脱轨评判标准将是以后重点研究的目标。
[1]俞展猷,李富达,李谷.车轮脱轨及其评价[J].铁道学报,1999,21(3):33-38.
[2]肖新标.轨道运动对列车脱轨影响的研究初探[D].成都:西南交通大学,2005.
[3]曾京.轮对稳态脱轨准则的研究[J].铁道学报,1999,21(6):15-19.
[4]薛弼一.轮对脱轨机理的研究[D].成都:西南交通大学,1998.
[5]王峰,曾树谷.以统计概率为基础的列车脱轨系数安全限值研究[J].铁道建筑,2012(1):110-112.
[6]凌复华.突变理论及其应用[M].上海:上海交通大学出版社,1987.
[7]P.T.桑博德.突变理论入门[M].凌复华,译.上海:上海科学技术文献出版社,1983.
[8]阿诺尔德.突变理论[M].周燕华,译.北京:高等教育出版社,1990.
[9]赵松年,于允贤.突变理论及其在生物医学中的应用[M].北京:科学出版社,1987.
[10]王文俊.基于突变理论的IP网络异常行为检测机制研究[D].成都:电子科技大学,2009.
[11]郭君,刘清.基于突变理论的航运事故发生机理[J].水运管理,2008,30(4):25-28.
