模糊逻辑的程度化紧致性

杨国微

（天津城市建设管理职业技术学院，天津 300134）

在完备格的框架下讨论模糊语义的紧致性及其导出的模糊结论算子的紧致性之间的关系是模糊逻辑研究中的重要问题。［5］证明了在是党的条件下两种之间的等价性，在［1］中证明了模糊逻辑与二值逻辑类之间的等价关系。［4］中提出了以模糊逻辑代替二值逻辑作为模糊逻辑研究的元逻辑，并分析和研究了Pavelka逻辑［3］的程度化紧致性。本文首先给出了程度化模糊语义的二值表现形式以及程度化模糊语义的各种紧致性与二值模糊语义的紧致性之间的关系，最好从程度化模糊语义导出合适的程度化模糊语义结论算子。

（1）σ（X）X，

（2）如果X!Y，则σ（X）!σ（Y），

（3）σ（X）＝σ（σ（X）），

则称σ为F上的模糊结论算子。

X∈LF，GF，定义X｜G∈LF为：x∈G，（X｜G）（x）＝X（x），否则（X｜G）（x）＝0。λ∈L，定义λX为：x∈F，λX（x）＝λ。X∈LF称为有限的，如果supp（X）＝｛x：X（x）＞0｝是有限的。

定义2 （1）F上的模糊语义结论算子σ称为紧致的，若X∈LF，x∈F，存在有限的GF，使得σ（X）（x）＝σ（X｜G）（x）。

（2）F上的模糊语义结论算子σ称为是程度化紧致的，若X∈LF，x∈F，σ（X）（x）＝∨｛σ（X｜G）（x）：有限的GF｝。

命题1 紧致的模糊结论算子是程度化紧致的。

定义3 （1）ΠL（LF），若F≠Π，则Π称为F上的程度化模糊语义。（2）设m，v∈LF，则m是v的模型的程度为

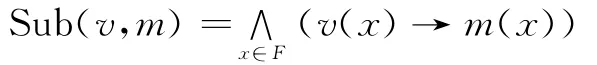
（3）Π－可满足初始赋值之模糊集Sat（Π）∈L（LF）为

（4）程度化模糊语义Π称为紧致的，如果v∈LF，x∈F，存在有限的v＇v使得

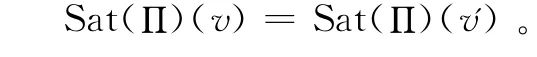
（5）程度化模糊语义Π称为程度化紧致的，如果v∈LF，有

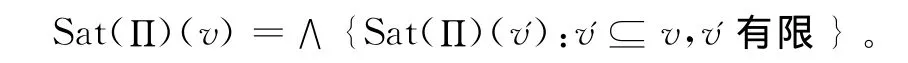
（6）程度化模糊语义Π称为程度化逻辑紧致的，如果对任意定向集族VLF，有

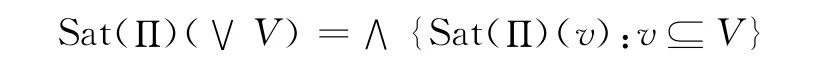
命题2 Sat（Π）关于Π是闭包算子。

定义4 设T∈L（LF），如果m，v∈LF，均有

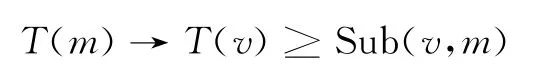
则称T关于可满足性封闭。

命题3 设T＝｛T：T关于可满足性封闭｝，T对任意交封闭。

定理1 对任意Π∈L（LF），Sat（Π）＝∧｛T：TΠ，T关于可满足性封闭｝。

证明 令D＝Sat（Π）＝∧｛T：TΠ，T关于可满足性封闭｝，v∈LF，首先证Sat（Π）（v）!D（v），设TΠ，T关于可满足性封闭，则m∈LF有

由条件TΠ知

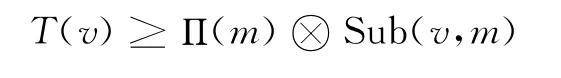
因为m是任意的，所以

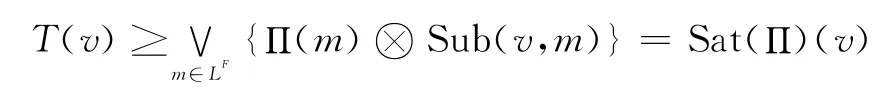
由T的任意性，有Sat（Π）!D。

其次证明Sat（Π）D，由Sat（Π）关于Π是闭包算子知Sat（Π）Π，又m，v∈LF

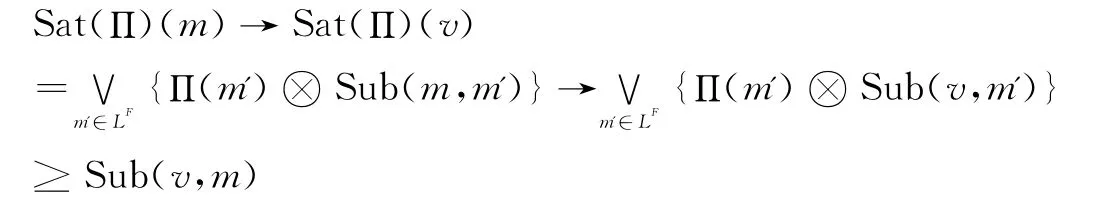
因此有Sat（Π）D，综上有D＝Sat（Π）。

定义5 设Π∈L（LF），α∈L，定义Πα＝｛v∈LF：Π（v）α｝。

命题4 Π∈L（LF），

F上的一个L－推理规则指的是一个序对r＝（r＇，r″），其中r＇是F上的n元偏函数，r″是上的按每个变元保任意并的n元运算。若v∈LF且对任意（x1，…，xn）∈Dom（r＇），

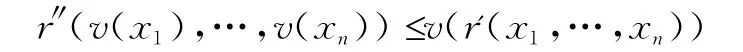
则称v对于规则r封闭，设R是F上的一集L－推理规则，如果对任意r∈R，v都关于r封闭，则称v对于R封闭。F上的语法指的是一个序对Σ＝（A，R），其中A∈LF称为公理集，R是L－推理规则集。

命题5 设Σ＝（A，R）是F上的L－语法，定义ΓΣ：LF→LF如下：X∈LF

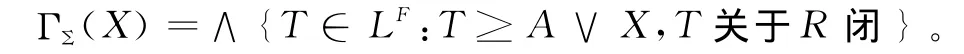
则ΓΣ是F上的闭包算子，称为由Σ导出的模糊结论算子。

Σ导出的模糊结论算子可以用程度化证明来刻画：

定理3［3］设Σ＝（A，R）是F上的L－语法，X∈LF，x∈F，

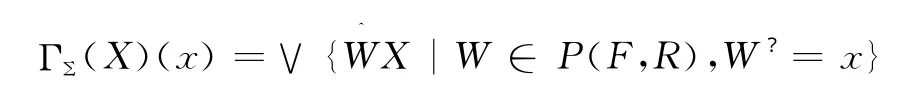
关于程度化证明的详细论述可参看［6］。

定义6 若有抽象公式Contra∈F，Π是抽象语义，对任意v∈Π，有v（Contra）＜1，则称Π是C－正则的；若Σ＝（A，R）是F上的L－语法，设A（Contra）＝0，则称Σ是C－正则的，Contra称为抽象矛盾公式。

设Contra∈F，X∈LF，令ΔΣ（X）＝ΓΣ（X）∨X（Contra）F.

定理4［4］若Σ是和谐的且对任意r∈R

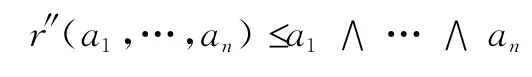
则ΔΣ是上的模糊推论算子。

定义7［4］ΔΣ的不动点称为F中的Σ理论，若它不等于F，则称为一致的；（2）F上的所有一致的Σ理论之集ΠΣ称为在F中的自然语义。

定义8［4］设Σ是模糊语法，则它在F上的程度化自然语义Π＇Σ∈L（LF）定义如下：对任意v∈LF，当ΔΣ（v）＝v时，Π＇Σ（v）＝Sub（v，F）→0，否则Π＇Σ（v）＝0。

命题6 如果Σ满足定理4的条件，并对任意的r∈R及a1，…，an，b1，…，bn∈L，

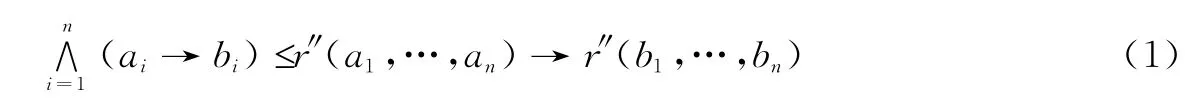
定义T0∈L（LF）为T0（v）＝Π＇Σ（Δ（v）），则T0关于可满足性封闭且T0Π＇Σ。

定理5［4］如果Σ满足定理4的条件以及（1），则Π＇Σ是程度化紧致的。

下面定义新的可满足性模糊集，并讨论其紧致性。

定义9 设Π∈L（LF），对任意X∈LF，令

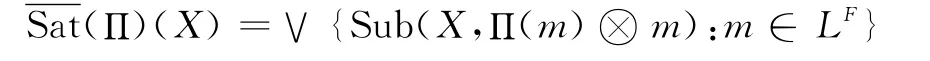
命题7 如果剩余蕴涵x→y对保任意并，则是闭包算子。

定义10 设Contra∈F，Σ是模糊语法，则它在F上的程度化自然语义给出如下：对任意v∈LF，当ΔΣ（v）＝v时，否则

定理6 如果C－正则的和谐模糊语法Σ满足定理4中的条件，以及（1）和对任意r∈，b，a1，…，an∈L

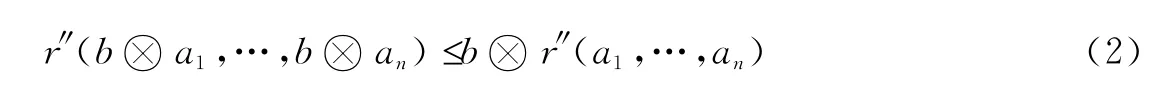
（II）注意到Σ的C－正则性及（2），施归纳法于程度化证明w的长度可知，对任意λ∈L，m∈LF，ΔΣ（λm）（Contra）!λΔΣ（m）（Contra）.

如果ΔΣ（m）＝m，则

如果ΔΣ（m）≠m，则所以

定义11 设ΠL（LF）是模糊语义，令σ：LFLF为称σΠ为由Π导出的程度化模糊结论算子。

命题8 σΠ是闭包算子。

命题9 如果L是紧的，则σΠ是程度化紧致的当且仅当σΠ是紧致的。

证明X∈LF，

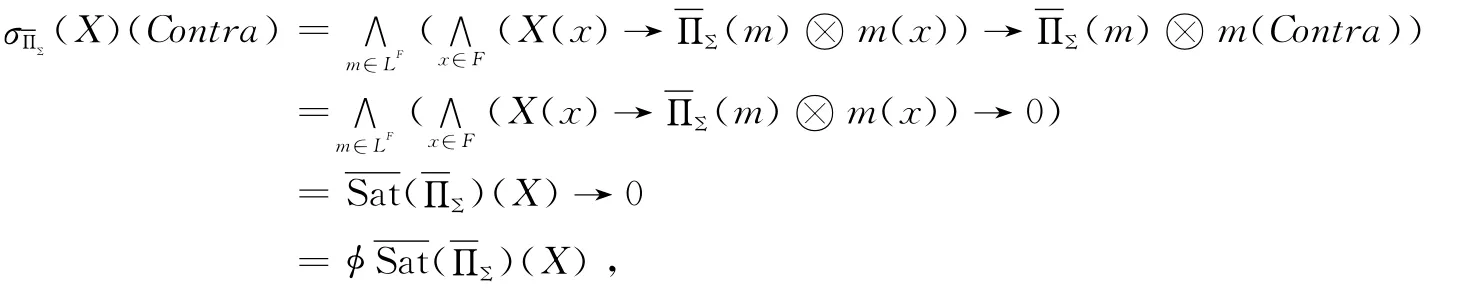
［1］Castro J.L.Fuzzy logics as families of bivaluated logics，Fuzzy Sets and Systems，1994，64：321－332.

［2］Gerla G.An extention principle for fuzzy logic.Mathematical Logic Quarterly，1994，40：357－380.

［3］Pavelka J.On fuzzy logic I，II，III，Zeischr.f.Math.Logik.und Grundlagen d.Math，1979，25：35－52，119－134，447－464.

［4］应明生.模糊逻辑的紧致性［J］.科学通报，1998，43（4）.

［5］王国俊.关于模糊语义的若干定理［J］.科学通报，1999，44（12）.

［6］王国俊.非经典数理逻辑与近似推理［M］.北京：科学出版社，2000.