空气动力学临界隧道交会理论与仿真研究＊

何德华，陈厚嫦，张 岩，黄成荣

（1 中国铁道科学研究院 机车车辆研究所，北京100081；2 铁道部运输局，北京100844）

我国高速铁路各速度级线路隧道的截面积和线间距已经确定，而隧道长度分布在几十米至数十公里的一个极大范围内。由于列车在不同长度隧道内运行和交会时压力波变化会有较大差别，尤其是隧道内交会呈现出很强的不确定性，因此，探索临界交会（包括隧道长度和动车组进入时差）与列车长度、速度等变量的关系，对于列车运行安全评估、车辆和隧道设计等都有非常重要的意义［1］。国外对于该问题的研究采用针对不同长度的隧道按均匀长度差值和进入隧道时差，仿真计算出各隧道长度和进入隧道时差列车上的气压波动曲线，然后再找出影响瞬变压力的临界隧道长度及时差［3］。此方法需每个速度级、每一隧道长度、每一列车进入隧道时差计算一条压力变化曲线，计算量大；国内梅元贵［4］等学者在各自专著中给出了定性的结论，王建宇等人［5-6］根据压力波的传播、反射和叠加规律，提出了单线隧道相应于压力上升和下降等情况的"最不利隧道长度"的计算图表及公式。

针对情况更为复杂的隧道交会情况，首先分析了影响隧道压力波峰值的因素，并根据压力波叠加原理，研究产生最大压力变化幅值临界交会的隧道长度和进出时差关于列车长度、运行马赫数的计算方法；并通过三维隧道交会数值仿真模型，对在京沪线大量运营的16辆编组某型动车组350km／h等速临界隧道交会工况进行了模拟，获得了该型动车组350km／h等速临界隧道交会时不同部位压力波波形以及变化幅值的量值。

1 临界交会隧道长度计算方法

在隧道内交会时，两列动车组的头部和尾部进入隧道时，会分别产生压缩波和膨胀波并在隧道内叠加。根据低速空气动力学中马赫波的传播规律和叠加原理，列车在隧道内交会时，动车组外表面压力波由以下几部分构成：①两列动车组头部进入隧道产生的压缩波及其在隧道另一端反射形成的膨胀波；②两列动车组尾部进入隧道产生的膨胀波及其在隧道另一端反射形成的压缩波；③两列动车组交会时邻线动车组引起的表面压力变化，由于单列动车组在隧道内运行时头尾车变截面之间的中间部位均为负压，因此交会时外表面压力主要呈下降趋势［1，3，7］。因此，影响隧道交会压力波大小的主要因素有隧道长度、动车组长度、列车速度、阻塞比和动车组头型等［1，2，7］。

对于以某一速度运行的两列确定长度动车组，选择一个合适的时差进入特定长度的隧道，将产生相同类型压力波碰在一起显著叠加的临界情况（压缩波与压缩波相叠加，膨胀波与膨胀波相叠加）。动车组交会产生的压力波在隧道内传播与叠加的机理如图1所示。图中Δt为两列动车组进隧道时差；实线表示压缩波，虚线表示膨胀波。由图1可知为使两列动车组在隧道内交会产生的压缩波得到完全叠加，需满足一列动车组头部进入隧道产生的压缩波在传过整个隧道后另一列动车组的尾部才进入隧道，即：

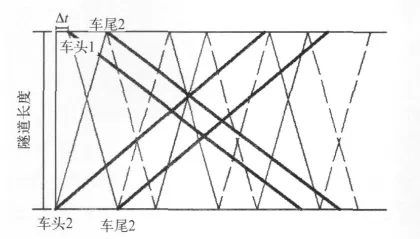
图1 导致车外压力变化最大幅值的临界隧道交会压力波理论图

同时，为使两列动车组在隧道内交会产生的膨胀波得到完全叠加，需满足动车组1头部进入隧道产生的压缩波在传过整个隧道时动车组2的尾部刚好进入隧道，即：

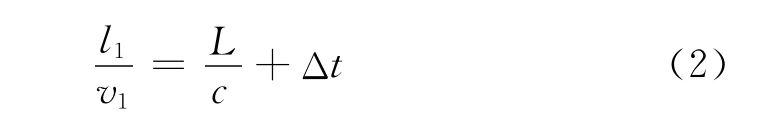
联立式（1）和（2）可得，在隧道内交会时，产生车外压力变化最大的两列动车组进入隧道的时差及隧道长度按式（3）和（4）计算。

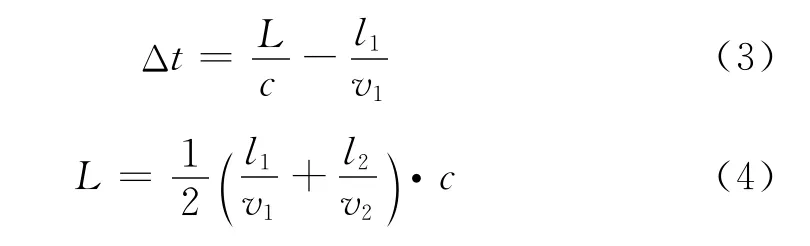
式中l2（m）和v2（m／s）为对面来动车组车长和车速；l1（m）和v1（m／s）为动车组车长和车速；L（m）为临界交会隧道长度；c（m／s）为声速。

通常，压力最大值出现在车头，是由两列动车组车头分别进入隧道产生的压缩波叠加而成；压力最小值出现在车尾，是由两列动车组车尾分别进入隧道产生的膨胀波，以及先进入隧道的动车组车头进隧道产生的压缩波经隧道端口一次反射后形成的膨胀波，以及两列动车组交会时的负压相叠加而成，因此，临界交会车外压力波曲线的最大负压往往会在数值上大于最大正压。

为方便使用，将我国常用动车组可能出现的导致车外压力变化最大幅值的等速临界隧道交会隧道长度计算出来，见表1。

表1 临界隧道交会隧道长度表

2 临界隧道交会三维仿真模拟

在导致车外压力变化最大幅值的临界隧道交会情况下，动车组车体表面所受到的气动载荷为极端气动载荷，该极端气动载荷的量值可以用来指导动车组的车体强度和车体密封性能设计，以及隧道结构及其附属设施的布置等。但式（4）所得的临界隧道长度计算方法仅限于确定临界隧道的长度，无法得到临界隧道交会过程中动车组表面的压力分布以及压力波的变化情况，更无从得到动车组头型、横截面形状等的影响，因此，对京沪高速铁路上运营的某型长编组动车组采用三维数值仿真方法临界隧道交会时车体表面的压力分布及变化幅值进行定量分析。

2.1 仿真模型

动车组模型16辆编组，长约400m，隧道长度1 400m，隧道断面积为100m2，并根据计算情况和符合真实物理模型的原则对动车组和隧道几何模型进行了表面光滑等合理简化。为考量极限情况纯粹临界交会的压力波大小，本计算模型未考虑隧道竖井、横通道和缓冲结构的影响。本次的计算区域为：车头前200m，车后350m，车身上方和左右各200m。隧道内交会的网格划分采取根据计算需要尽量提高网格效率的变网格密度方法，除动车组局部复杂区域外均采用结构化网格，并依据y+等参数对动车组、地面和隧道壁面等划分边界层，网格总量约1 800万个，集成后交会网格如图2所示。

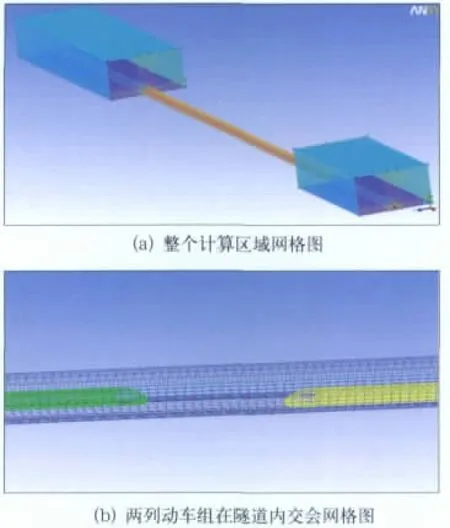
图2 动车组在隧道交会时网格图

交会计算采用地面不动，两动车组以350km／h速度相对运行的方式设定计算条件。动车组为无滑移壁面，地面为固定无滑移壁面，明线交会外场为压力出口，给定标准大气压101 325Pa。本次计算采用商业软件fluent进行，湍流模型为标准k-ε，并使用标准壁面函数对壁面进行处理，控制方程选用可压缩的Navier-Storks方程：

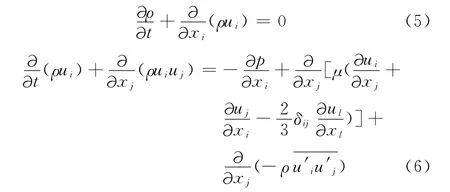
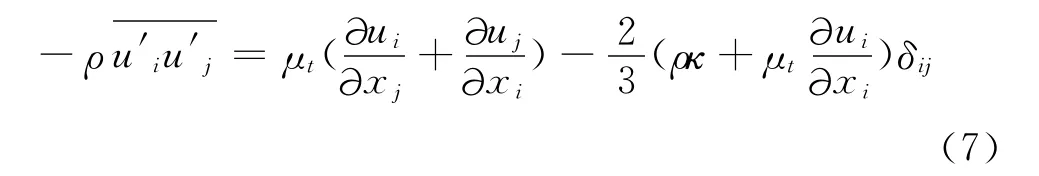
对于标准k-ε模型，增加的湍流动能k和ε湍流耗散率的输运方程如下：

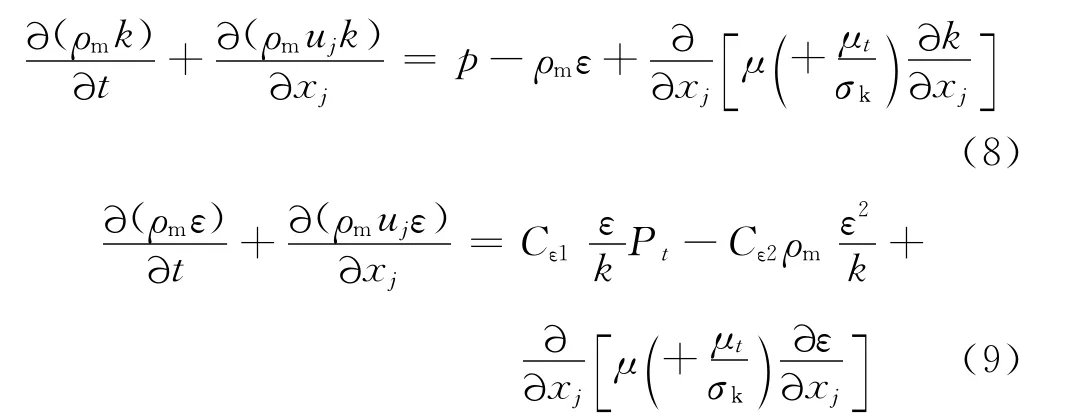
结合公式（6）和（7），涡黏系数可表示为：

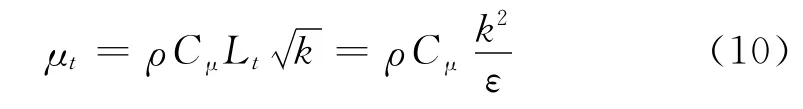
式中k和ε分别为湍动能和湍流耗散率，Pt为湍动能生成项，μt为湍流粘性系数，Cε1、Cε2、σε、σk、Cμ等为模型常数。

2.2 模型验证

为了验证所建立的动车组隧道通过空气动力学计算模型，包括模型选取和参数设置等，将武广试验中CRH3C型高速动车组以350km／h通过石门岭隧道的测试数据与数值计算结果进行比较。实车试验与数值计算尾车中间窗边的压力变化曲线如图3所示。从实车试验结果与数值计算的比较结果可见，压力波变化趋势、变化幅值等基本一致。实车试验中，压力变化曲线波动比较大是因为受到转向架、复杂形状和不光滑表面，以及动车组振动等因素的影响。仿真计算与实车试验的对比结果表明，仿真计算的计算方法基本上能准确地反映动车组隧道内交会时的压力波变化规律。从而验证了物理模型、计算方法和计算程序的正确性，可用于接下来的临界交会计算。

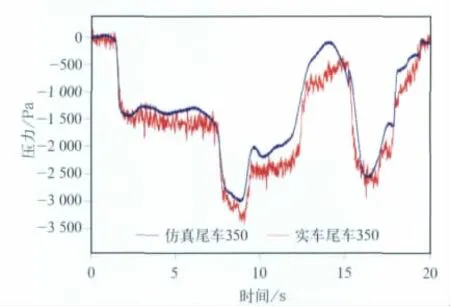
图3 实车试验与数值计算中尾车中部压力变化曲线比较图

3 数值模拟结果与分析

为了获得列车典型位置的压力变化情况，并对动车组压力变化沿纵向的变化规律进行分析，在动车组几何模型上布置40个监控点（从尾车至头车对称布置在动车组外表面，如图4所示）进行压力时域变化数据的输出。

图4 压力输出监控点布置图

图5为动车组头车，8车和尾车测点的压力波曲线，由图可知无论是头车、中间车、还是尾车，各测点中相同类型的压力波都得到了充分的叠加，从而使得压力变化最大值、最小值和变化幅值都很大。表2给出了动车组导致车外压力变化最大幅值的临界隧道交会过程中部分监控点压力变化最大值、最小值和变化幅值。由表2所列的检测结果可知，导致车外压力变化最大幅值的临界隧道交会过程中车外压力变化最大幅值高达9 885Pa。因此，极有可能造成车体可承受的载荷限值超出相关标准，有必要深入分析临界交会问题，以避免安全隐患。

图6～图8分别为动车组进入隧道头尾车压力、交会出现的最大正压和最大负压时刻的压力云图，由图6可知：车头部位和一些干扰部件处为正压、司机室上方弧顶为负压，动车组中间部位压力分布均匀。由于司机室前窗与车体存在小幅倾角，因此，在车头位置形成次高压区，该压力分布与明线运行一致，这进一步验证了计算模型的正确性；由图7可知最大正压为10 100 Pa；由图8可知最大负压为-8 180Pa，分别比进入隧道前的5 311Pa和-4 305Pa大了几乎一倍，表明压力波得到了充分叠加。

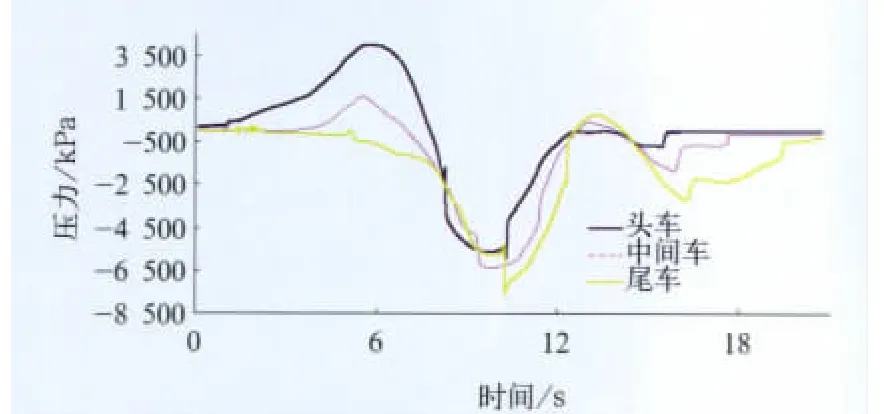
图5 临界交会模拟计算压力波曲线

表2 监控点压力变化极大值、极小值和变化幅值

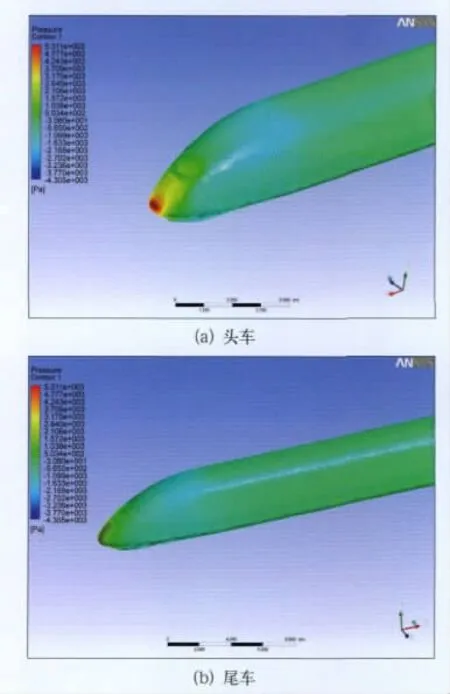
图6 进入隧道前头、尾车压力云图

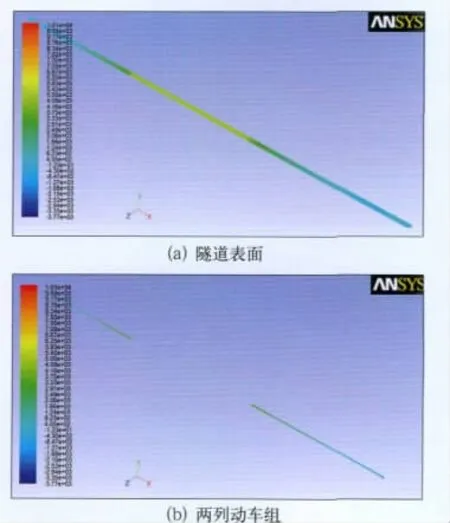
图7 交会出现最大正压时刻压力云图

由于计算条件所限，文章未对临界隧道长度附近的隧道按均匀长度差，以及临界隧道长的不同进入隧道时差进行计算，得出各工况下列车上的气压波动曲线，再找出瞬变压力的临界隧道长度及进入时差，从而进一步验证临界交会计算方法。

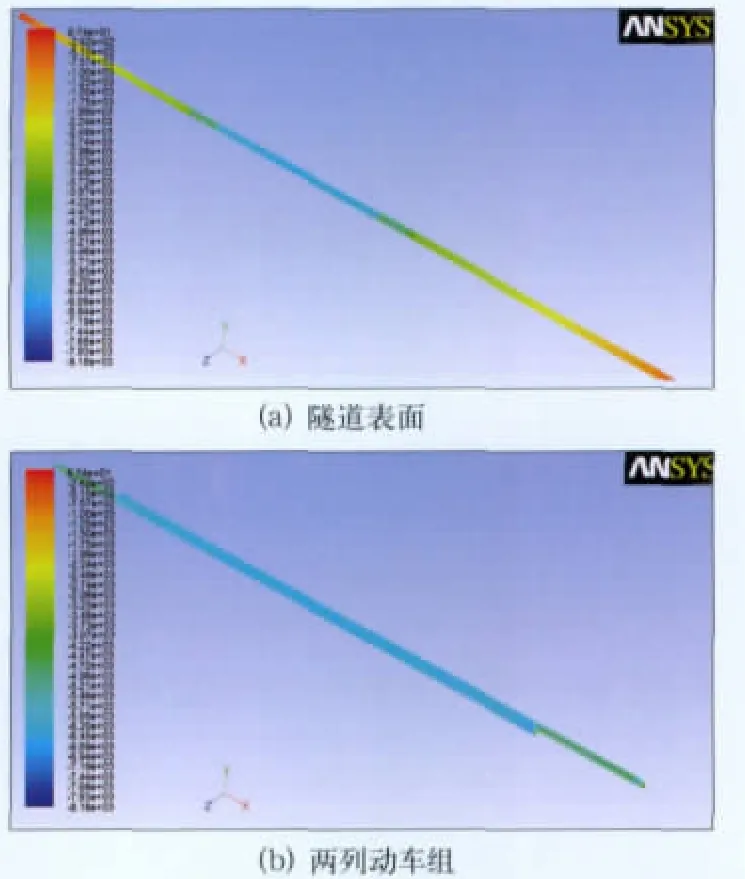
图8 交会出现最大负压时刻压力云图

4 结 论

（1）首先通过对列车隧道会车的影响因素进行理论分析，推导出了基于交会压力波最大变化幅值的隧道临界交会隧道长度和两列动车组进入隧道时差快速计算方法。对于京沪线常见的16辆编组350km／h等速会车，两列车同时进入隧道的情况下压力最大最小值对应临界隧道长度均约为1 399m。

（2）建立了CRH3型动车组隧道通过和交会的数值模拟计算模型，并用实车试验压力波数据对动车组隧道通过的模型进行了验证，结果表明，仿真计算的计算方法基本上能准确地反映动车组通过隧道的压力波变化规律，验证了物理模型、计算方法和计算程序的正确性。

（3）通过实车试验数据验证过的三维数值仿真模型，对京沪线常见的16辆编组350km／h等速会车进行了计算，从监控点的情况可知各位置的压力波得到了充分的叠加，车头部位的压力变化幅值为9 885Pa。该结果在验证了基于交会压力波最大变化幅值的隧道临界交会隧道长度和两列动车组进入隧道时差快速计算方法的正确性的同时，也表明需对临界交会问题进一步深入分析，并在以后的动车组车体强度和车体密封性能优化设计以及隧道结构优化设计、隧道内附属设施的布置中，充分考虑极端工况下的特殊气动载荷。

［1］京沪综合试验研究总报告之空气动力学分报告TY字第3074-1号［R］.北京：中国铁道科学研究院，2011.

［2］武广客运专线隧道气动效应试验研究报告TY字第2704号［R］.北京：中国铁道科学研究院.2009.

［3］EN 14067-5，Railway Applications-Aerodynamics-Part 5：Repuirements and Test Procedures for Aerodynamics in Tunnels［S］.2003.

［4］梅元贵，周朝晖，许建林.高速铁路隧道空气动力学［M］.北京：科学出版社2009.

［5］王建宇，万晓燕，吴剑.隧道长度对瞬变压力的影响［J］.现代隧道技术，2008，45（6）：1-4.

［6］TB1003-2005.铁路隧道设计规范［S］.北京：中国铁道出版社，2005.

［7］Schetz J A.Aerodynamics of High-Speed Trains.Annu Rev Fluid Mech［J］.2001，33：371-414.