等效锥度的计算及验证＊

2013-11-27董孝卿林凤涛王悦明

铁道机车车辆 2013年1期

吴宁，董孝卿，林凤涛，文彬，王悦明

（1 中国铁道科学研究院机车车辆研究所，北京100081；2 华东交通大学载运工具与装备省部共建教育部重点实验室，江西南昌330013）

轮轨几何接触是解释铁道车辆动力学性能的基础，等效锥度是轮轨几何接触中的重要参数。当铁道车辆运行在直线线路或大半径曲线线路上时，等效锥度决定着轮轨之间的匹配程度［1-2］。

对我国多条线路上的动车组振动状态及车轮磨耗跟踪研究的结果表明，轮轨匹配等效锥度的大小与动车组运行过程中的动态响应密切相关。如等效锥度过小导致动车组运用过程中出现晃车现象［3-4］，等效锥度过大引起动车组车辆构架横向振动报警［5］。因此，定期获取运用动车组车轮廓形并准确计算等效锥度是很必要的。

在关于轮轨关系的研究领域内，等效锥度是一个重要参数。等效锥度与铁道车辆的动力学性能有着密切的联系，欧洲标准UIC518［6］将等效锥度作为车辆型式试验的关键参数并规定了试验过程中等效锥度的范围。国内铁道车辆领域内很多研究工作探讨了等效锥度和车辆动力学性能的关系［7-11］。文献［12］比较了几种等效锥度计算方法的差别。

对于确定的轮轨廓形和参数，等效锥度的计算结果应该是确定的。等效锥度算法并不局限于一种，且计算结果受轮轨廓形平滑插值方法影响较大。因此需要有相关验证标准对等效锥度算法进行验证，一种等效锥度算法只有在完全通过相关标准验证后其计算结果才能被认可。欧洲标准EN 15302用于等效锥度算法的验证［1］，UIC519给出了等效锥度的计算方法［2］。

1 等效锥度的定义

锥形踏面轮对在线路上具有相对固定的正弦运动轨迹，Klingel理论指出这一运动轨迹的波长取决于轮对踏面的锥度角以及左右轮轨接触斑之间的距离，即Klingel公式：

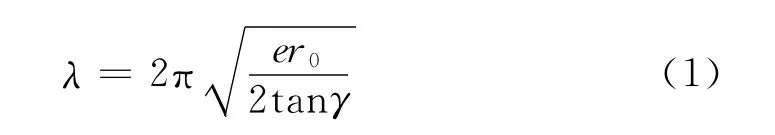
式中λ为轮对运动轨迹的波长，m；e为左右轮轨接触斑之间的距离，即为跨距，m；r0为轮对处在对中位置时的车轮滚动圆半径，m；γ为车轮踏面的锥度角，弧度。

实际运用中的车轮踏面具有变化的锥度角，可以采用对左右车轮滚动圆半径差（取决于轮对横移量）进行积分的方法获得轮对的运动波长，再将该波长与Klingel理论中的相应波长对照，得出轮对等效锥度。即：

式中tanγe为等效锥度。

等效锥度定义为给定轮对运动波长相同的锥形车轮轮对的车轮锥度角正切值。如图1所示。

图1 等效锥度定义

等效锥度的实质是非锥形踏面轮对在每一横移幅值下均等效于一个锥形踏面轮对。其等效的依据是两者的运动轨迹波长相等。

2 等效锥度的计算方法

等效锥度计算的流程见图2。主要分为以下几个步骤：（1）对轮轨廓形进行平滑和插值处理；（2）根据轮轨廓形和位置参数计算得到轮轨接触点；（3）根据轮轨接触点得到与轮对横移量对应的左右车轮滚动圆半径差；（4）基于左右车轮滚动圆半径差计算结果，计算等效锥度。

图2 等效锥度计算流程

以上4个步骤中，每一步均可采用不同的计算方法。步骤（1）可选择采用通用的数学平滑插值处理方法，步骤（2）和步骤（3）采用的计算方法均为一般意义上的解析几何方法。以下简要由滚动圆半径差计算等效锥度步骤（4）的2种方法（图3）。

方法1：半径差函数线性回归算法。根据滚动圆半径差积分确定轮对横移幅值和横移量的对应关系，再由横移幅值对应的横移量确定滚动圆半径差的线性回归范围，对该范围的滚动圆半径差进行线性拟合，拟合后的斜率之半即为对应轮对横移幅值下的等效锥度。

方法2：非线性微分方程积分算法。根据滚动圆半径差积分确定轮对横移幅值和横移量的对应关系，再由边界条件（即横移幅值对应的最大横移量和最小横移量对应的摇头角Ψ均为0）计算求解摇头角Ψ时的常数C，得到常数C后积分确定摇头角Ψ与横移量y的函数，之后再进行积分，确定出轮对横移幅值对应的轮对运动波长λ，最后由公式（2）得到等效锥度tanγ。

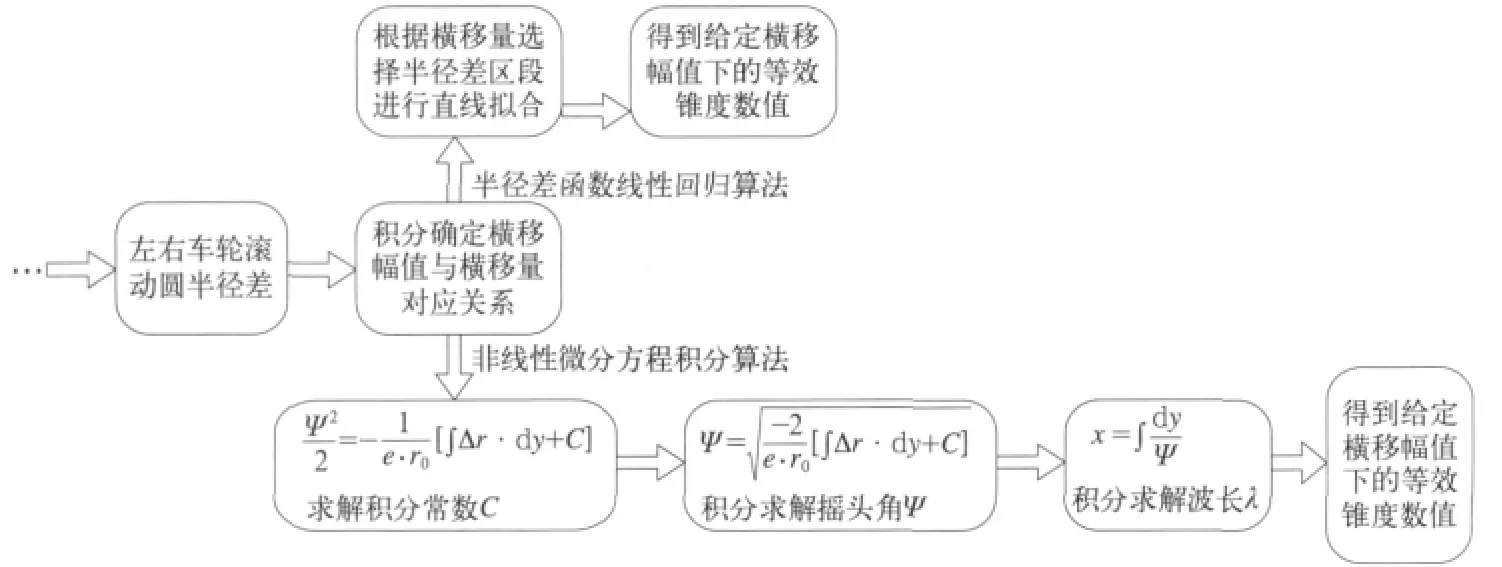
图3 由滚动圆半径差计算等效锥度的2种算法

3 等效锥度算法编程实现

根据上面介绍的等效锥度计算方法，采用方法1实现了等效锥度计算的算法编程，以适应批量计算实测轮轨廓形等效锥度的需要。

（1）轮轨廓形的插值平滑处理

轮轨廓形的插值平滑处理主要根据轮轨廓形坐标数据及轮轨几何参数（轨距，轮对内侧距，轨底坡等）实现轮轨廓形坐标的插值、平滑及轮轨位置定位。采用两次插值处理，一次平滑处理实现轮轨廓形坐标插值平滑处理：先对初始轮轨廓形坐标值进行插值处理，接着对插值处理后的坐标进行平滑处理，最后再对平滑处理后的坐标进行插值。其中平滑处理采用滤波的方法实现。插值平滑处理完成后根据最终的轮轨廓形坐标及轮轨几何参数输出用于计算轮轨接触点的左右侧轮轨廓形坐标。

（2）计算轮轨接触点

采用左右侧轮轨垂向距离最小极值的方法计算轮轨接触点，具体的计算流程见图4。轮对横移量一般从-20mm计算到20mm。左右侧轮轨最小垂向距离之差绝对值的控制变量ε是一个很小的正数，其值越小，轮轨接触点的计算精度越高。但若ε过小，则可能得到错误的轮对侧滚角，从而得到错误的轮轨接触点。ε的选择与轮轨插值点横向坐标间距有关，如轮轨插值点横向坐标间距取0.1mm时，ε可取0.01mm。图5为计算得到的轮轨接触点示意图。

（3）计算左右车轮滚动圆半径差

在得到轮轨接触点后，根据轮对横移量对应的左右车轮上接触点可直接得到左右车轮滚动圆半径差。

（4）根据左右车轮滚动圆半径差计算等效锥度

等效锥度的实质是非锥形踏面轮对在每一横移幅值下均等效于一个锥形踏面轮对，等效锥度是轮对横移幅值的函数，因此首先要确定轮对横移量和轮对横移幅值的对应关系。

确定半径差为0时对应的横移量yem，该横移量对应的轮对位置即为轮对相对于轨道的平衡位置。对半径差进行积分，积分S（y）=-∫Δr·dy分别从yem向横移量正方向y+和负方向y-各进行一次，确定出在轮对横移振幅ym下轮对的最小横移量yemin和最大横移量yemax。对最小横移量yemin和最大横移量yemax之间的半径差进行直线拟合，拟合得到的斜率之半即为轮对横移振幅ym下的等效锥度。

图4 轮轨接触点及计算流程

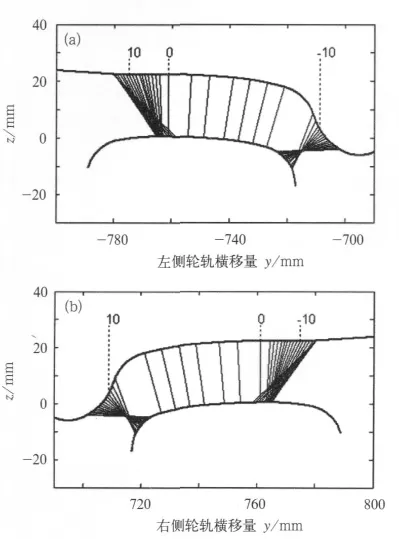
图5 轮轨接触点示意图

如果Δr=f（y）特征在区间［yemin，yemax］内关于原点对称性较差，应对每部分（正和负）分别进行回归得到两个等效锥度值tanγe，p和tanγe，n，等效锥度可通过下式得到：

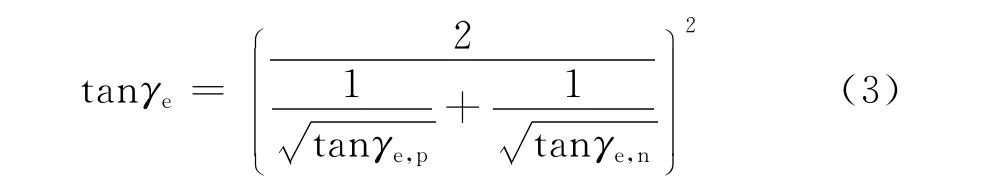
4 等效锥度算法的验证

由于计算等效锥度可采用不同的计算方法，且计算等效锥度的每一步均可选取不同的数学算法。对于确定的轮轨廓形及轮轨参数，等效锥度计算结果应是确定的、稳定的。因此必须采用相关标准对整个等效锥度算法进行验证。一个具体的等效锥度算法只有完全通过相关标准验证后才能用于实测轮轨廓形等效锥度的计算。

欧洲标准EN 15302：2008规定了验证等效锥度算法的过程、验证采用的基准轮轨廓形及采用基准轮轨廓形计算得到的等效锥度基准结果和容许误差。采用EN 15302：2008对整个等效锥度算法程序进行验证。整个验证过程共分为3步。

（1）采用EN 15302：2008附录中给出的基准轮轨廓形数据及匹配参数作为输入，考核被验证的算法程序的计算结果是否在规定的容许误差界定范围内。其目的是考核计算程序能否准确地计算出等效锥度，即验证计算程序的准确性。图6给出了一个验证结果示例，本例中左侧车轮廓形为标准附录中的车轮B廓形，右侧车轮为标准附录中的车轮A廓形，轨道廓形为标准附录中的轨道A廓形。图中同时给出了ADAMS软件轮轨接触计算模块的计算结果。

图6 等效锥度算法程序验证第1步图例

（2）将EN 15302：2008附录中定义的随机误差添加到基准轮轨廓形数据中，考核被验证算法程序的计算结果是否在规定的容许误差界定范围内。其目的是当考核轮轨廓形有一定误差时计算程序的计算结果是否稳定，即验证计算程序的稳定性。图7给出了一个验证结果示例，本例中车轮廓形为标准附录中的车轮A廓形，轨道廓形为标准附录中的轨道A廓形。

图7 等效锥度算法程序验证第2步图例

（3）将EN 15302：2008附录中定义的栅格误差添加到基准轮轨廓形数据中，考核被验证的算法程序计算结果是否在规定的容许误差界定范围内。其目的是考核轮轨廓形数字化过程中引入栅格误差后计算程序的计算结果是否稳定，即验证计算程序能否用于实测轮轨廓形等效锥度的计算。图7给出了一个验证结果示例，本例中车轮廓形为标准附录中的车轮A廓形，轨道廓形为标准附录中的轨道A廓形。