用于强震记录仿真地动位移的高精度累积数值积分方法研究1
2013-11-26曲保安刘希强范晓勇于庆民赵银刚
曲保安 刘希强 蔡 寅 范晓勇于庆民 赵银刚 张 明 李 峰 孙 豪
1)山东省地震局泰安基准地震台,泰安 271000
2)山东省地震局,济南 250014
3)中国地震局地球物理研究所,北京 100081
4)山东省地震局安丘地震台,潍坊 262100
5)山东省地震局烟台地震台,烟台 264000
引言
地震预警用P波前3s记录波形估算震级和烈度需要用到卓越周期和峰值位移等参数(Wu等,2006;2008),卓越周期的计算和峰值位移的量取都需要位移记录,而目前的数字地震计为速度或加速度记录,如何将速度记录和加速度记录积分为位移记录是一个必须面对的难题,尤其是对于需要两次积分的加速度记录,其积分后的位移记录的正确性和精确性一直被怀疑(Chen等,2007;Emore等,2007)。
关于利用强震加速度记录积分为位移记录的研究,早在20世纪40年代就已经开始。自1933年在加州长滩地震中记录到第一条强震动加速度记录以来,关于用强震加速度记录估算近断层同震位移的研究得到了深入的发展。但是,由于强震动记录受到地面倾斜、环境噪音等各种因素的影响,直接使用强震动加速度记录积分计算得到的速度和位移通常会出现严重的漂移失真现象,因此需要对加速度记录进行专门的校正处理以便估算比较真实的同震位移,对于此方面的研究已经得到深入而广泛的认同和长足的发展(金星等,2005;于海英等,2009;彭小波等,2011)。但是关于用于地震记录数值积分方法本身的研究,却未受到足够的关注。
本文从数值积分方法本身的研究着手,首先对记录进行分段三次Hermite插值,客观上相当于用类似上采样的方式将采样率变为原始数据采样率的4倍,之后采用积分区间四等分的Newton-Cotes积分公式进行积分(李庆扬等,2000),并对实际强震动加速度记录进行了应用验证。
1 积分方法
在对强震动记录波形特征进行幅频分析并对数值计算方法和数值积分以及累积数值积分的多种方法进行学习分析的基础上,在目前对于累积数值积分只有梯形积分算法被广泛应用的现状,以及 Simpson、Romberg等多种数值积分算法和复合型数值积分方法得到深入研究的推动下,作者首先考虑采用n=4时的Newton-Cotes公式作为计算累积数值积分的方法,但是考虑到强震仪频带的高频截至 80Hz以及近场强震动记录信号覆盖高频部分,所以直接对原始强震记录进行累积数值积分计算可能导致信号高频损失过多,并且根据强震动记录波形的性质(郑君里等,2011),选择分段三次Hermite插值(李庆杨等,2000;2008;刘彬清等,2002;龙爱芳等,2013)。
1.1 插值
目前应用较为普遍的一维插值方法有四种:最近邻插值;线性插值;三次样条插值;分段三次Hermite插值(李庆扬等,2008)。作者用周期为2π的正弦函数,选择从0到10间隔为1的11个点,分别采用四种插值方法,插值后从0到10之间为41个点,绘制了四种插值方法的效果图(图1)。其中,圆圈为原始的11个点,菱形点为插值后的 41个点,线是为了直观展示而将41个点连接的连线。图1(a)为最近邻插值;(b)为线性插值;(c)为三次样条插值;(d)为分段三次Hermite插值。
根据强震动记录波形的性质(郑君里等,2011),选择对原始数据保真性较强而且平滑较好的分段三次Hermite插值。
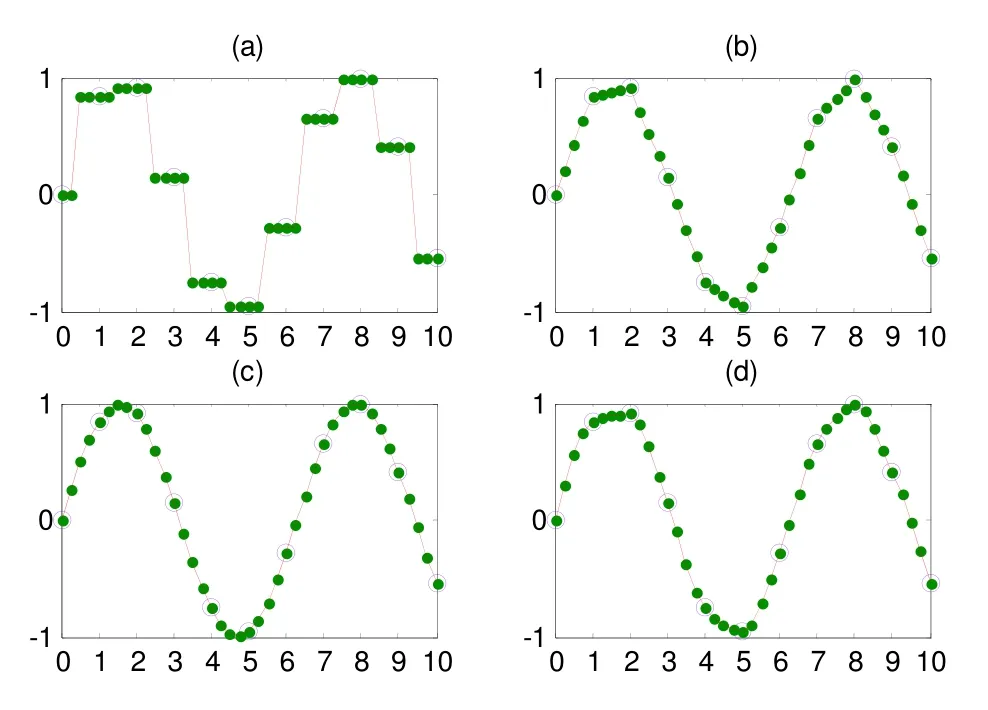
图1 四种插值算法插值效果图Fig. 1 Comparison of four interpolation algorithms
1.2 积分公式(李庆扬等,2008)
根据Newton-Cotes公式:
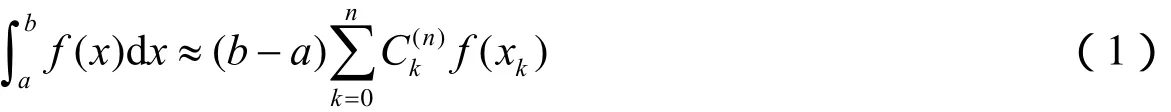
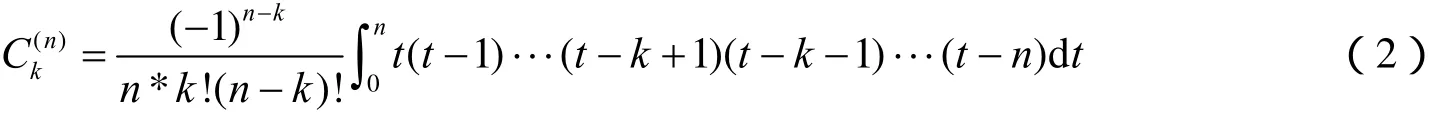
从计算精度和计算量两方面综合分析,本文选择n=4时的Newton-Cotes公式:
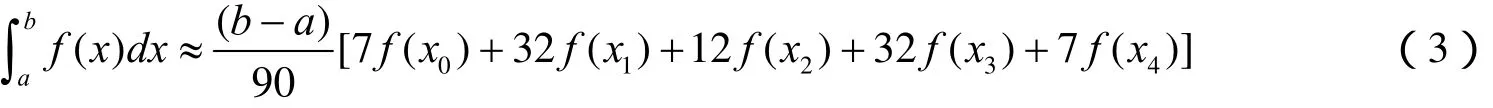
1.3 误差分析
当n=4时,Newton-Cotes公式计算结果具有5次代数精度,截断误差为:
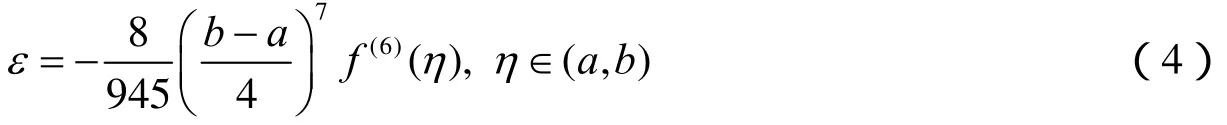
而当n=1时,Newton-Cotes公式为:
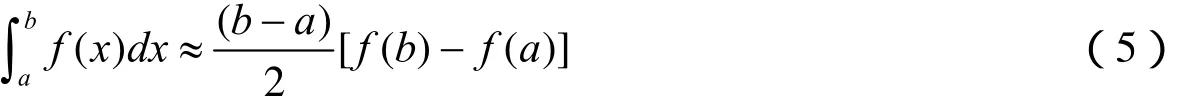
即为梯形积分公式,计算结果具有1次代数精度,截断误差为:

从公式(5)和(6)来看,n=4时,Newton-Cotes公式积分方法的误差比梯形积分精度高4个数量级。所以,梯形公式代数精度较低,Newton-Cotes公式的代数精度比梯形公式代数精度高,能更好地近似积分值(王少英,2012)
2 方法验证
为了验证本文提出方法的积分效果,采用构造的正弦信号和实际的强震动加速度记录分别进行积分效果分析。
2.1 构造正弦信号
构造周期为2π,采样率为10,长度为4π的正弦信号,按照本文方法的处理步骤,首先对构造信号进行插值,见图 2。其中,蓝色为原始构造信号,红色为插值后的信号,为了能够清楚分辨插值前后的变化,图2(b)对横轴[1,2]区间的信号进行了放大。
图3为构造信号经过一次和两次积分后产生的信号对比。其中,蓝色信号为构造信号,红色信号为经过一次积分后的信号,绿色为经过两次积分后的信号。对正弦信号进行一次积分,积分后信号为余弦信号,进行两次积分,积分后信号仍为正弦信号,但是变为负值。图3的结果与此吻合。
2.2 强震动加速度记录
为了验证本文累积数值积分方法对实际强震记录的适用性,选取2013年4月20日雅安芦山地震和2008年5月12日汶川地震的强震动加速度记录,采用原始梯形积分方法和本文方法分别对强震动加速度记录进行积分,分别比较二者两次积分的结果。
图4为宝兴地办强震台记录的2013年4月20日雅安芦山地震P波初至的前3s波形,对此强震加速度记录先去除均值,再插值,见图5。其中,蓝色为原始强震记录信号,红色为插值后的信号。图5(b)为更加清楚分辨插值前后变化,截取了图5(a)前0.2s的数据。
图6为分别用本文方法和梯形积分方法对强震记录进行一次积分的结果对比。蓝色为本文方法,红色为梯形积分方法。图6(b)为选取图6(a)末尾0.2s数据进行了局部放大。
图7为分别用本文方法和梯形积分方法对强震记录进行两次积分的结果对比。蓝色为本文方法,红色为梯形积分方法。图7(b)为选取图7(a)末尾0.2s数据进行了局部放大。
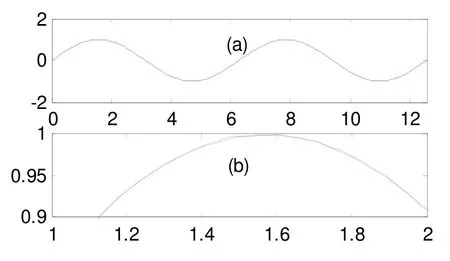
图2 构造信号插值前后对比Fig. 2 Comparison of constructed signal before and after interpolation
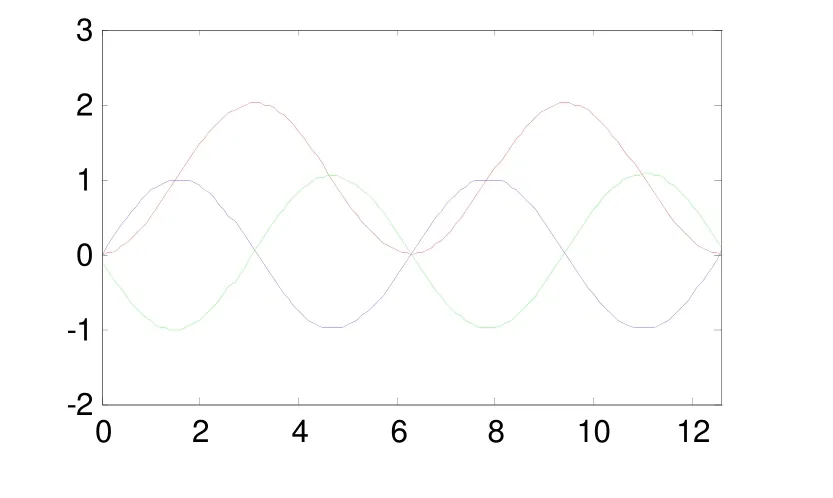
图3 构造信号与一次和两次积分后信号Fig. 3 Original structured signal and its integration signals after 1st and 2nd integration
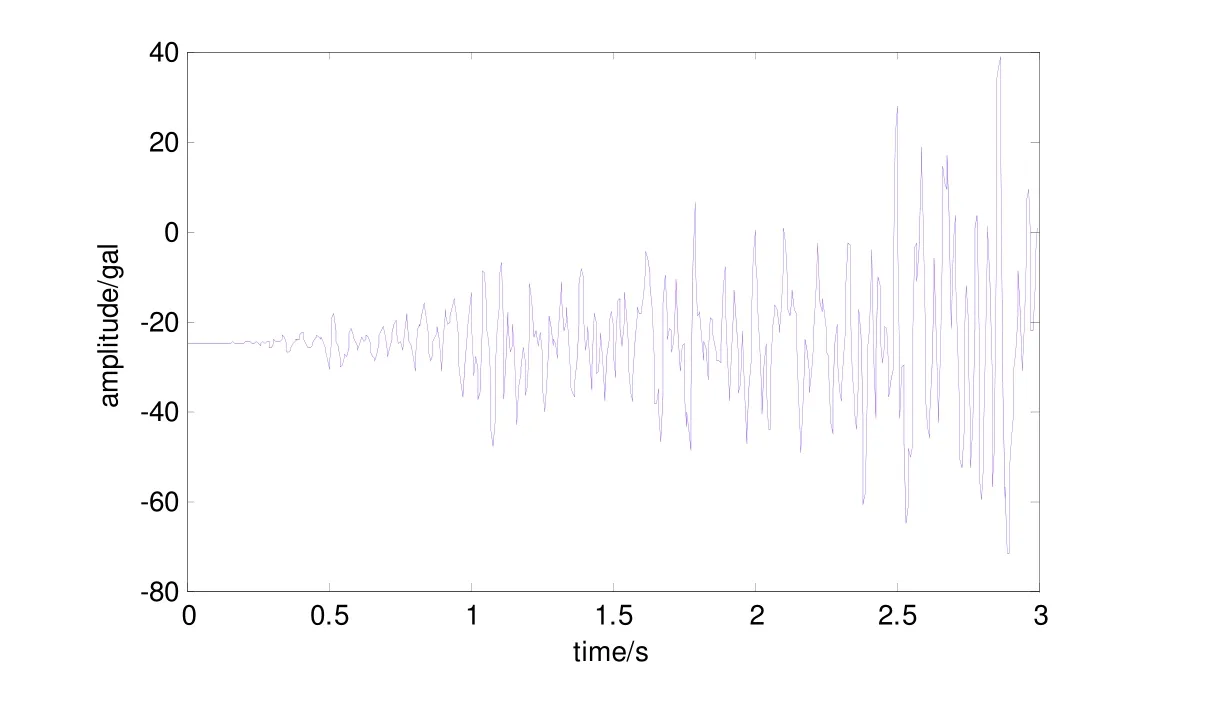
图4 宝兴地办强震台记录的2013年4月20日雅安芦山地震P波初至的前3s垂直向波形Fig. 4 The first three-second vertical component record of Yaan Lushan earthquake on Apr. 20, 2013 recorded at BXDB strong motion station
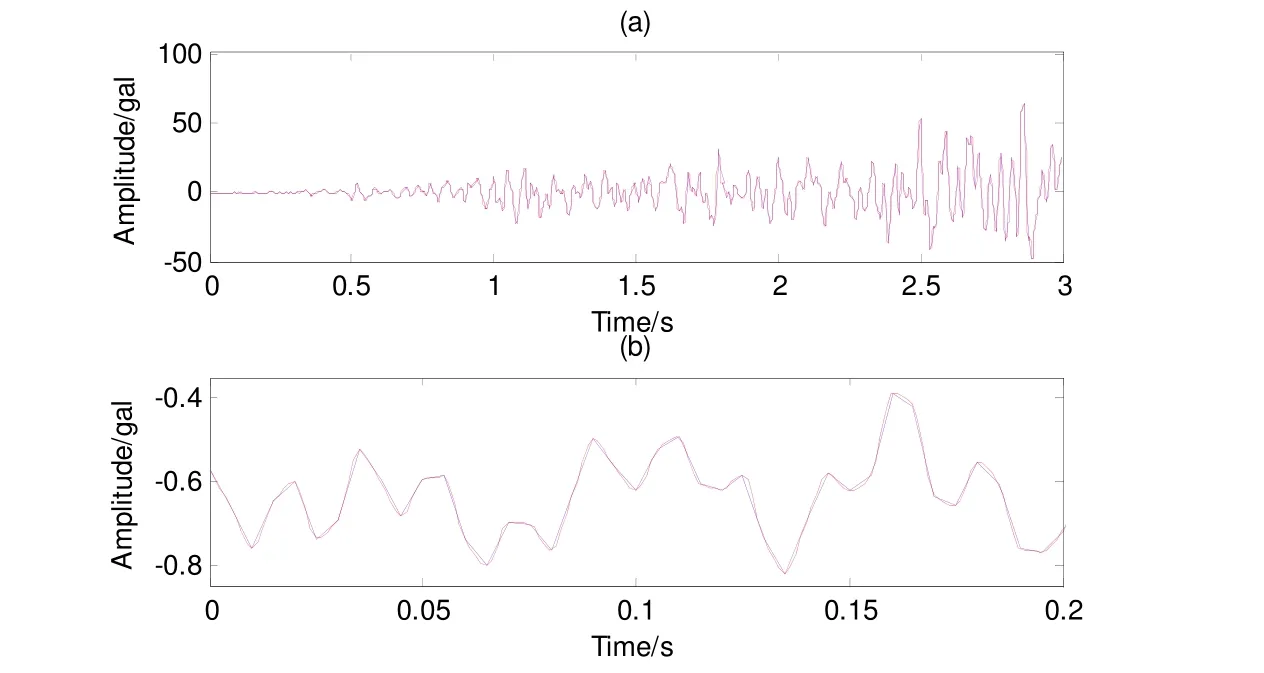
图5 雅安芦山强震加速度记录插值前后对比Fig. 5 Comparison of Yaan Lushan strong motion record before and after interpolation
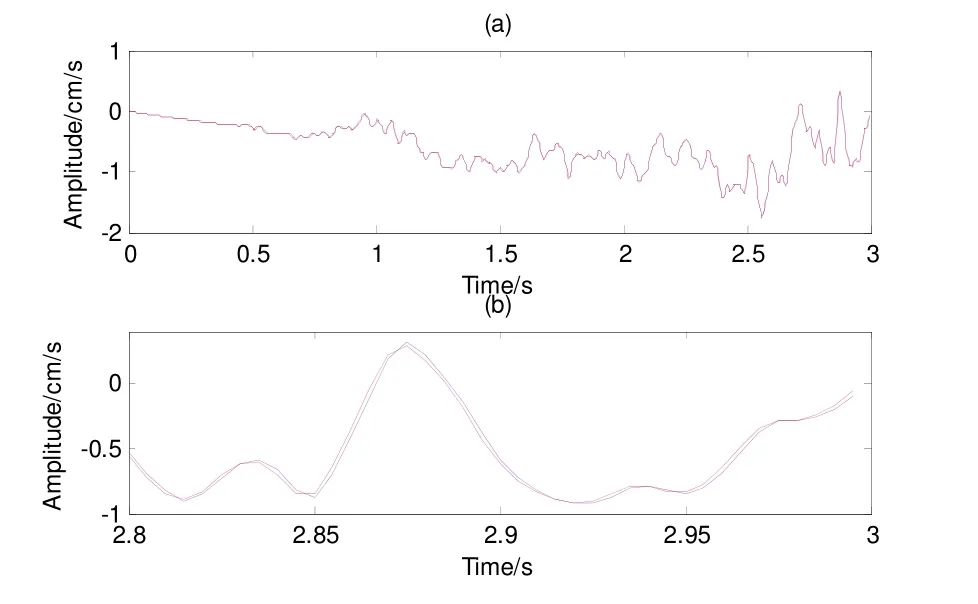
图6 两种积分方法对雅安芦山强震记录一次积分结果Fig. 6 The 1st integral results of strong motion records of Yaan Lushan earthquake with two different integration methods
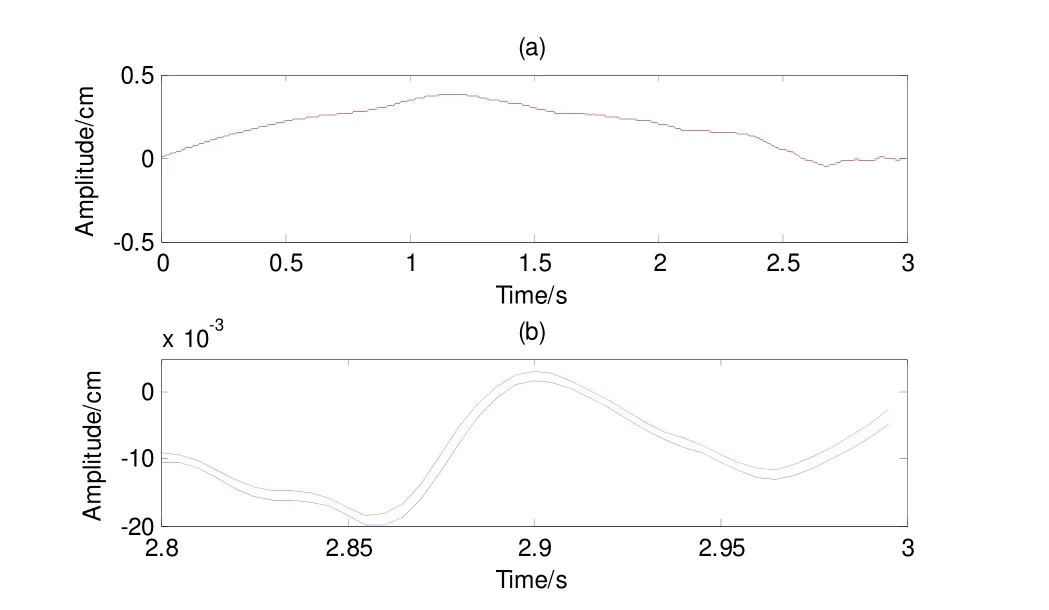
图7 两种积分方法对雅安芦山强震记录两次积分结果Fig. 7 The 2nd integral results of strong motion records of Yaan Lushan earthquake with two different integration methods
图8 为汶川卧龙强震台记录的2008年5月12日汶川地震P波初至的前3s波形,对此强震加速度记录先去除均值,再插值,见图 9。其中蓝色为原始强震记录信号,红色为插值后的信号。图9(b)为更加清楚分辨插值前后变化,截取了图9(a)前0.2s的数据。
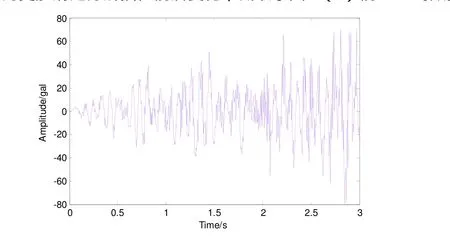
图8 汶川卧龙强震台记录的2008年5月12日汶川地震P波初至的前3s东西向波形Fig. 8 The first three-second horizontal east-west component record of Wenchuan earthquake on May. 12, 2008 recorded at WCW strong motion station
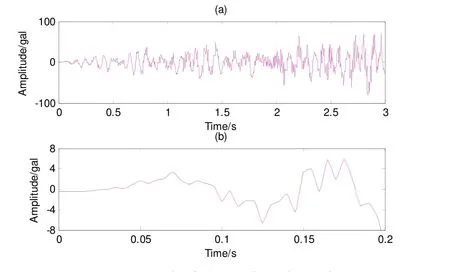
图9 汶川强震加速度记录插值前后对比Fig. 9 Comparison of strong motion record of Wenchuan earthquake before and after interpolation
图10 为分别用本文方法和梯形积分方法对强震记录进行一次积分的结果对比。蓝色为本文方法,红色为梯形积分方法。图10(b)为选取图10(a)末尾0.2s数据进行了局部放大。
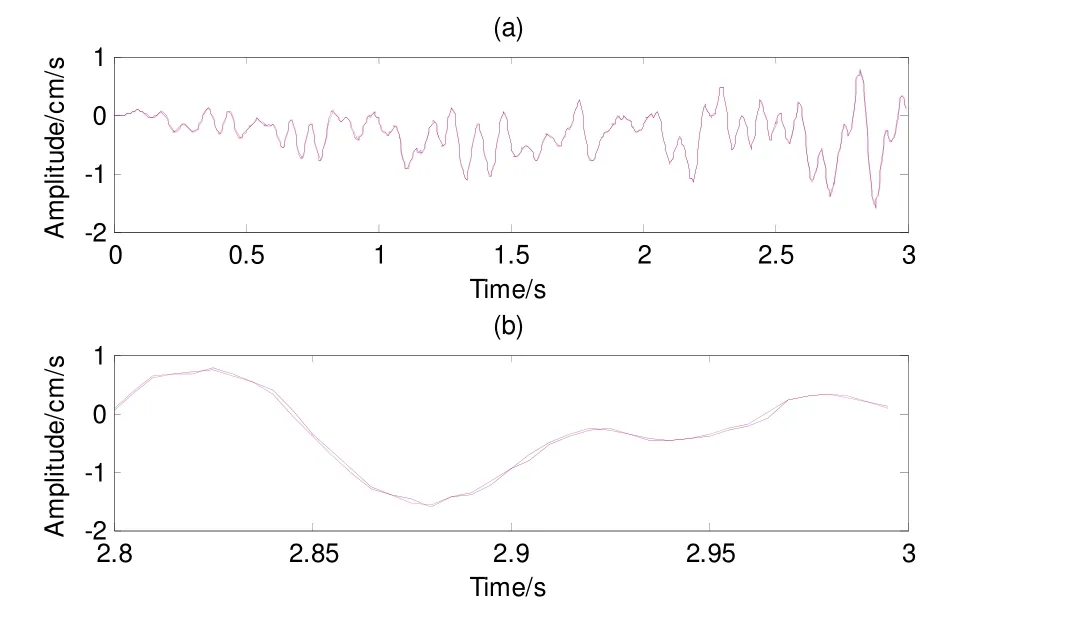
图10 两种积分方法对汶川强震记录一次积分结果Fig. 10 The 1st integral results of strong motion records of Wenchuan earthquake with two different integration methods
图11 为分别用本文方法和梯形积分方法对强震记录进行两次积分的结果对比。蓝色为本文方法,红色为梯形积分方法。图11(b)为选取图11(a)末尾0.2s数据进行了局部放大。
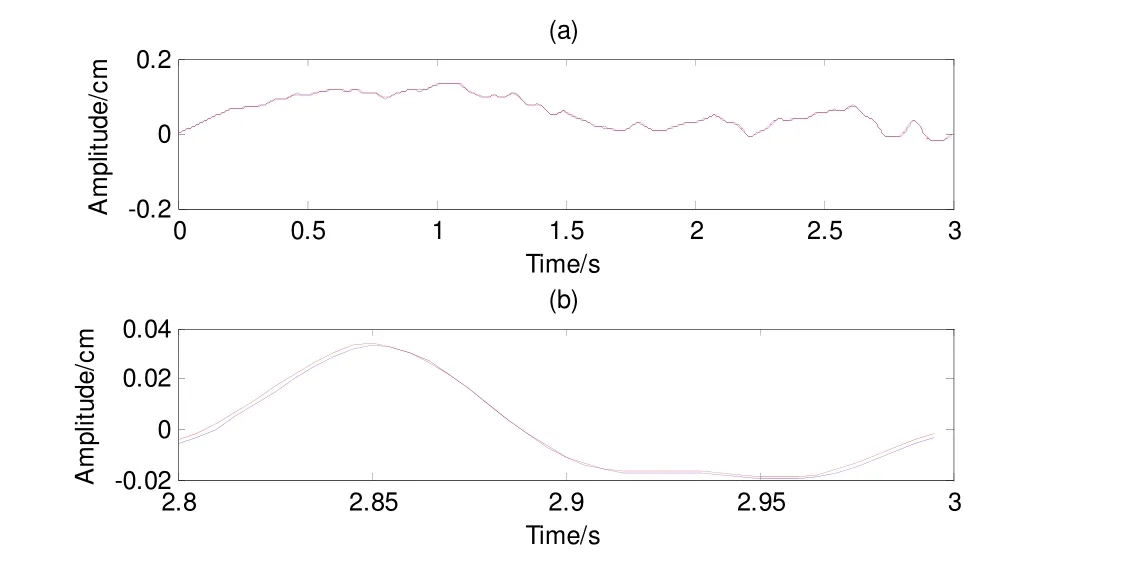
图11 两种积分方法对汶川强震记录两次积分结果Fig. 11 The 2nd integral results of strong motion records of Wenchuan earthquake with two different integration methods
从图6(a)、图7(a)、图10(a)和图11(a)来看,本文积分方法与梯形积分方法积分结果基本一致。但从图6(b)、图7(b)、图10(b)和图11(b)来看,两种积分方法的结果有一定的差值,但是差值较小。我们认为差值来自两个方面:一是插值所引入的;二是积分方法的精度不同造成的。
经过用两种方法对11个强震台站记录的2013年4月20日雅安芦山地震33个通道的加速度记录和3个强震台站记录的2008年5月12日汶川地震9个通道的加速度记录的两次积分的结果对比,我们发现本文的积分方法与梯形积分方法积分结果均有一定差值,但差值较小。
3 讨论
本文仅限于积分算法本身的研究,然而从强震加速度记录积分为位移记录需要去除漂移,导致零线漂移的原因多种多样,去除漂移的方法也各有不同,这些内容本文均未涉及。
用本文方法计算的结果与传统梯形积分方法有一定的差值,但是由两种积分方法的差值引起的卓越周期和峰值位移的差值大小,以及根据峰值位移和卓越周期计算的震级的差值大小尚未知,需要通过积累大量强震加速度记录震例进行计算统计分析验证。
4 结论
本文提出了一种累积数值积分方法,首先对被积信号进行分段三次Hermite插值,将插值后的信号长度变为原信号长度的4倍,之后采用积分区间四等分的Newton-Cotes积分公式进行积分。
经过误差分析以及对构造信号和实际强震加速度信号的验证,本文积分方法的精度高于梯形积分方法,而且正确可靠,适用于将强震动加速度记录积分为位移记录。
金星,马强,李山有,2005. 利用数字强震仪记录实时仿真地动位移. 地震学报,27(1):79—85.
李庆杨,关治,白峰杉,2000. 数值计算原理. 北京:清华大学出版社,251—282.
李庆扬,王能超,易大义,2008. 数值分析. 北京:清华大学出版社.
刘彬清,任亚娣,2002.Newton-Cotes数值求积公式的渐近性. 上海大学学报(自然科学版),8(6):503—506.
龙爱芳,胡军浩,2013. 基于Hermite插值的高精度数值积分公式. 华侨大学学报(自然科学版),34(3):349—352.
彭小波,李小军,刘启方,2011. 基于强震记录估算同震位移的研究进展及方法. 世界地震工程,27(3):73—80.
王少英,2012. 数值积分若干方法的比较分析. 德州学院学报,28(6):14—19.
于海英,江汶乡,解全才等,2009. 近场数字强震仪记录误差分析与零线校正方法. 地震工程与工程振动,29(6):1—12.
郑君里,应启珩,杨为理,2011. 信号与系统. 北京:高等教育出版社.
Chen S.M., Loh C.H., 2007. Estimating permanent ground displacement from near-fault strong-motion accelerograms. Bulletin of the Seismological Society of America, 97 (1): 63—75.
Emore G.L., Haase J.S., Choi K. et a1., 2007. Recovering seismic displacements through combined use of 1-Hz GPS and strong-motion accelerometers. Bulletin of the Seismological Society of America, 97 (2): 357—378.
Wu Y.M., Kanamori H., 2008. Development of an earthquake early warning system using real-time strong motion signals. Sensor, 8:1—9.
Wu Y.M., Zhao L., 2006. Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning. Geophysical Research Letters, 33 (L16312): 1—4.
