一种改进的蚁群聚类算法在客户细分中的应用

宋中山，周 腾，周晶平

(中南民族大学计算机科学学院，武汉430074)

人们通过对大自然中社会性动物有组织的行为进行数学建模，提出了群体智能算法［1］，如猴群算法、鱼群算法及蚁群算法等，这些群体智能算法使得人类的研究摆脱了固定的模式，大胆地用于解决复杂的组合优化问题，为人工智能的发展开辟了一条新的道路.

20世纪90年代，Dorigo M等人提出了蚁群算法［2］，最早被应用于解决旅行商问题［3］，还运用于二次调度问题，并结合数据挖掘中的聚类算法，应用于很多复杂的实际问题中［4-6］.但是，蚁群算法中参数的设置往往凭借于经验，时常出现易陷入局部最优等问题.人们通过对蚁群算法的研究，发现蚁群算法的很多特性与聚类分析问题的求解方式都比较相似，当把蚁群算法和聚类分析结合使用用于求解问题时，往往比单一使用聚类分析技术所得到的结果好很多［7，8］.

本文针对传统的蚁群聚类算法中参数设置依赖于经验的指导以及蚂蚁移动随机性大等问题，提出一种改进的自适应蚁群聚类算法，该算法与标准的蚁群聚类算法相比，去除了参数对聚类结果的影响，降低蚂蚁移动的随机性以加快聚类的速度.银行存在大量的客户数据，将蚁群聚类算法应用于银行客户细分，有利于对客户关系进行管理.

1 蚁群聚类算法

蚁群聚类算法可分为4类:以信息素为指导，根据蚂蚁觅食行为来聚类;根据蚂蚁习性，以自身形成一堆为指引的行为实现聚类;依据蚂蚁尸体堆积原理聚类;根据可以相互识别并创建不同巢穴的原理实现聚类.

Lumer和Faieta把Deneubourg等人提出的基本模型进行推广，运用到数据分析领域，使用实值元素来聚类数据向量，提出了LF算法模型［9］，主要思想是:首先将待处理的数据随机散放在一个Z×Z的2维网格中，同样也产生一些虚拟的蚂蚁，每个网格单元中只能分布一个数据对象.d(Oi，Oj)表示网格中的两个对象Oi和Oj之间的距离，也称为相似度，一般使用欧式距离，若这两个对象为同一个对象，则d(Oi，Oj)=0，否则 d(Oi，Oj)=1，进而可以得到一个相似度矩阵.设N只蚂蚁在此网格上运动，都是随机捡起或放下某个数据对象，若在某时刻在r位置蚂蚁找到了数据Oi，则它的局部密度表示为:

其中Neights×s(r)为单元r的邻域面积，α为相异度因子，它决定了数据对象之间的区分度，α越大区分度越小，反之亦然，s2表示蚂蚁可以观察到以r为中心的s×s范围内分布的所有数据对象.若蚂蚁没有负载，则随机捡起一个邻近单元中的数据对象，其概率为公式(2);若蚂蚁有负载，则随机选择邻近一个空的单元中，将该数据对象放下，其概率为公式(3).

其中k1，k2为阈值常量.

相似密度的大小制约着蚂蚁捡起或放下的概率，当相似度小时，放下的概率小，捡起的概率大，蚂蚁容易将数据转移;反之亦然.

从而判断背负的对象与观察到的对象是否相似，对象Oi在地点r处通过相似度计算，从而不断拾起或放下对象.重复这一过程，直到达到算法最初设置的最大迭代次数，算法结束.而数据对象最终在2维网格中的分布情况就是聚类的结果［10］.

2 自适应蚁群聚类算法

蚁群聚类算法在求解的过程中，主要存在两个问题:随机选择策略大大减缓了算法的进化速度;正反馈原理的根本是为了得到更好的解，但是容易出现停滞现象.人们对蚁群聚类算法中随机参数的状态转移和信息素进行研究，主要可以通过以下策略进行自适应调节.

(1)随机参数q0的自适应调节.为了避免出现停滞现象，在蚂蚁移动过程中动态调整转移概率.就是让蚂蚁以q0选择距离长度短或者信息素浓度较高的节点，以1－q0来进行概率式搜索.

(2)信息素挥发度ρ的自适应调节.信息素挥发度ρ的设置影响到蚁群算法搜索时间的长短以及能否得到全局的最优解.使用1－ρ表示信息残留因子，它间接衡量蚂蚁个体间相互影响大小的尺度.若将ρ的最初大小置为1，即ρ(0)=1，使用ρmin表示ρ的最小值，如果蚁群算法某个时刻已经求得了一个解，而这个解在后面的N次循环内没有较大变化时，即当0.95ρ(t－1)≥ρmin时，将此时的 ρ置为 0.95ρ(t－1);否则将ρ置为ρmin.通过这种方式对信息素挥发度不断进行自适应调节.在算法求解过程中，为了提高蚁群算法的查找速度，加大全局搜索的能力，在每次循环结束后，求出此时的解，并保存.

(3)通过比较某处蚂蚁与其周围8个邻居的相异度，记录蚂蚁前一个运动状态，所处的坐标及附属的类号，可以通过公式(4)定义自适应度函数:

其中d(ai，aj)表示蚂蚁代表的数据对象i和j之间的距离，一般使用欧几里德距离，而参数αij可由公式(5)确定.

蚂蚁所属的类可根据以下规则进行更新.

(1)当某个蚂蚁到达一个合适的位置而转变成睡眠态时，将它所属的类号更改为与它相异度最小的类号;

(2)若蚂蚁由睡眠态变为活跃态，则将其类号改为它在移动过程中的类号;

(3)若蚂蚁保持睡眠态不变，则其类号不变.

3 改进的蚁群聚类算法

为了解决传统蚁群聚类算法中容易出现停滞现象和易陷入局部最优的问题，本文从以下3个方面对算法进行改进.

(1)公式(1)说明了相似度衡量的方式，其中参数α的值对聚类的结果具有较大的影响，它表示相异度因子，它的值没有范围，可以达到任何值，因此参数α值的设置往往依赖于经验指导，如果缺乏相关的经验，很难保证聚类结果的准确.由于相似度衡量的标准主要由各模式间的距离决定，由公式(1)可以看出，相似度的大小与模式间的距离成反比，当各模式间的距离越小的，所得的相似度越大，反之亦然.依此，本文采用一种更直接的方法，去除α，直接使用公式(6)来表示模式Oi与其局部环境中其他模式的相似度.

通过公式(6)可以看出，f(Oi)与模式间的距离成正比，即f(Oi)的值越大，说明模式Oi与模式Oj间的距离越大，表明模式Oi与其它模式的相似度越小.公式(6)去除了参数α对聚类结果的影响，使得模式的相似度与距离的关系更加明显，并且不需要经验的指导.

(2)在标准蚁群聚类算法中，蚂蚁的前进方向是随机选择的.这种随机选择的方法，当某只蚂蚁长时间承载一个模式，如果找不到合适的位置，会使它一直承载而不放下，或者当蚂蚁放下一个模式后再次选择时，一直没有模式可以选择而长时间处于空闲状态.研究发现，当对待处理数据进行主成分分析后，发现整体的聚类效果已初步形成.如果蚂蚁再次选择随机移动，很可能导致蚂蚁后面的多次移动都是无效的，因为蚂蚁移动的下一个位置，极有可能该邻域内模式数据极少甚至没有模式，这将严重阻碍蚂蚁放下或拾起模式进度，对聚类结果造成影响.针对这些问题，本文采用一种基于网格化的运动方式，通过前后坐标对比，判断蚂蚁的状态，如果处于运动，并且需要丢弃模式时，使蚂蚁有选择性地往较多模式的地方运动，从而降低蚂蚁移动的随机性，加快收敛速度.

(3)去除概率转换函数的使用，引入相似度阈值F，通过对f(Oi)与阈值F比较，判断蚂蚁下一步的运动状态是移动还是静止.这种处理方式简单而且容易实现，可以避免概率转换函数中因参数设置不准确而对聚类的结果造成较大的影响.随机移动会增加算法的处理时间，在这里使用一种局部最近邻移动原则来改善蚂蚁的移动.一只蚂蚁Oi的局部最近邻就是在其局部环境中，与该蚂蚁最相似的蚂蚁，用Ok表示，则它们之间的关系可以表示为:

蚂蚁的移动具有方向性，使得它始终朝着信息素强度高的地方移动.由于阈值F直接影响蚂蚁下一步的状态，因此在实际运算中，必须取合适的值.如果F过大，会导致蚂蚁一直处于静止状态，如果过小，又会导致蚂蚁一直移动，找不到合适的位置休息.在这里采用一种自适应调整阈值的方法.

蚂蚁只有移动和静止2种状态，用m1表示移动状态下蚂蚁的数量，用m2表示静止状态下蚂蚁的数量.通过记录前一次迭代时蚂蚁的位置和再次迭代后蚂蚁的位置的比较来判断蚂蚁是移动还是静止.假设总的蚂蚁数量为N=m1+m2，N也可以表示聚类模式的个数，如果处于移动状态的蚂蚁与处于静止状态的蚂蚁比例几乎持平，表明阈值合适，如果m1比例比较大(大于总数的85%)，则阈值设置过小，应该适当加大，反之，如果m2比例比较大，则阈值设置过大，应该适当减小.在本文中，每迭代50次，统计移动了的蚂蚁的数量值，而F的大小通过公式(9)进行调整.

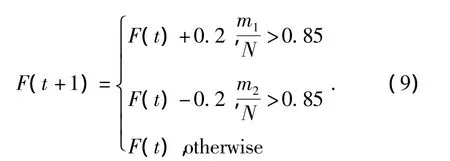
改进后算法的具体步骤如下.

步骤1:初始化各个参数，包括最大循环次数T_MAX，蚂蚁的个数N，邻域半径r，相似度阈值F等.

步骤2:对待聚类模式进行主成分分析，然后对选取其中的两个主成分进行一定的处理并作为投影坐标［11］.这两个主成分必须保留模式的大部分信息，以便经过投影后，相近的模式之间的距离较小而挨得比较近.投影完毕后将所有的蚂蚁投影到2维网格上，并赋给每个蚂蚁一个初始的坐标.

步骤3:循环以蚂蚁Oi的此处坐标为中心，r为半径，按照公式(6)计算相似度的方式，计算该蚂蚁在当前所处的环境中的相似度.对比此时阈值F(t)与当前相似度f的大小，如果F(t)大于或等于f，蚂蚁静止;否则，按公式(8)中表示的局部最近邻原则，重新将蚂蚁置为新的坐标值.

步骤4:计算每50次迭代后计算m1和m2的值，然后再按照公式(9)调节相似度阈值F(t).再回到步骤3，直到达到最大迭代次数退出.

步骤5:根据所得的结果计算各类的聚类中心，输出各聚类的模式.

4 在客户细分中的应用

客户细分是指依照客户的属性进行划分的客户集合，它不仅是客户关系管理的重要理论组成部分，也是其重要管理工具之一［12］.它在管理客户的分类、预测有价值的客户、有效分配人力或物力以及成功执行相关政策等基本原则中发挥着重要的作用，并使得企业能够充分清晰地了解客户，从客户的需求出发，制定相应的决策.总的来说，客户细分就是指企业根据现有的发展方向和市场的定位与走势，依据企业对客户个人资料的分析，按照某种或某些属性对客户的种类进行划分，并提供个性化的商品和服务的过程［13］.

银行客户细分的原理是首先对现有的客户信息收集和整理，然后依据客户的属性，按照某一条件对客户进行分类，最后银行管理者针对不同类别的客户制定不同的策略和服务，如图1所示.

图1 银行客户细分原理Fig.1 Theory of bank customer segmentation

本文所使用的数据来源于某银行对客户的数据记录，该数据库中存在大量个人存款及消费记录，每条记录都代表了持卡人的基本资料，例如:客户编号，姓名，年龄，证件号码，手机，工作单位名称，住址，月薪及存款等.对数据进行预处理，删除一些缺失或错误的信息，并从中抽取1000条记录，去除与实验无关的数据属性，例如姓名，性别，证件号码，手机号等属性，只保留几项重要属性如年龄、工作年限、客户月薪、存款及借贷情况，将1000条记录分成5类，结果分配如表1所示.

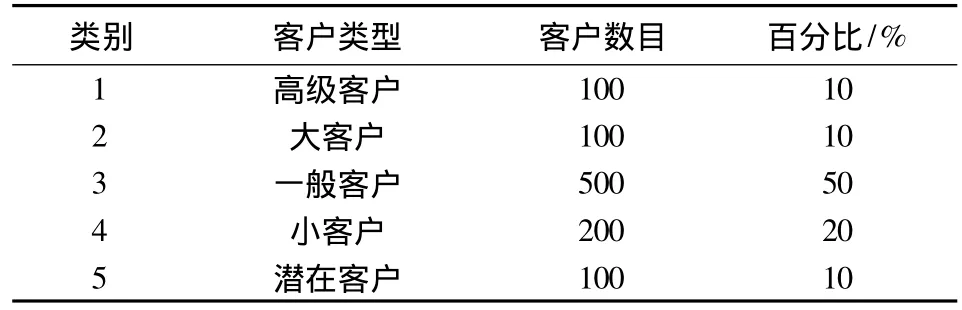
表1 客户类别分配Tab.1 Distribution of customer categories

K均值聚类算法是数据挖掘中一种比较健壮的算法，因其处理速度快，常被用于处理客户细分，在此运用K均值聚类算法对刚分配的数据集进行识别，处理结果如表2所示.

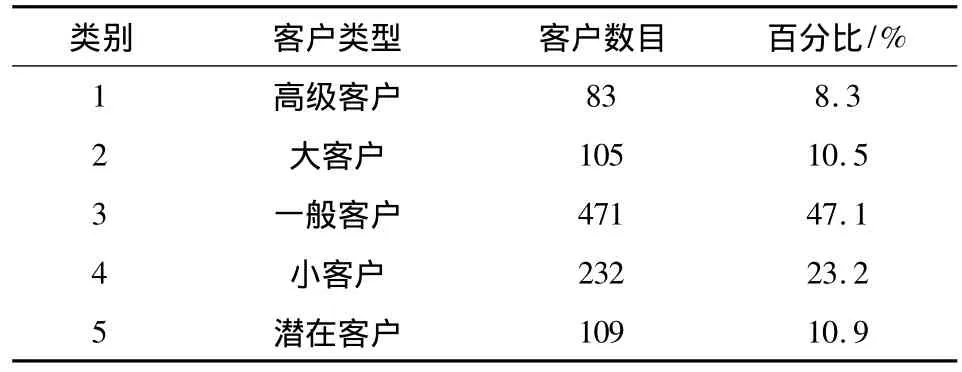
表2 K均值聚类算法识别客户类别Tab.2 Customer segmentation through K-means clustering algorithm

利用MATLABR2009a作为开发软件，运用改进后的算法对数据集进行识别，处理结果如表3所示.

表3 改进算法识别客户类别Tab.3 Customer segmentation through the improved clustering algorithm

统计K均值聚类算法与改进算法对银行客户细分的处理时间和结果，可得到如表4所示的对比结果分析.

表4 两种算法的对比结果Tab.4 Comparison of the results through two algorithms

从表4可以看出，使用K均值聚类算法对银行客户进行细分时，时间要优于改进算法，通过对K均值聚类算法的原理进行分析发现，发现它的处理时间短缘于它过早陷入了局部最优，不能发现全局的最优，通过各类客户中数据的统计，改进后的算法在正确率方面明显优于K均值聚类算法，表明该算法可以用于处理银行客户细分问题.

5 结束语

本文提出的改进算法简化了参数，避免了参数对聚类结果造成的影响，在聚类过程中，通过引入自适应策略，动态调整蚂蚁的状态，减少蚂蚁移动的随机性，加快了聚类的过程.同时，蚂蚁在移动过程中通过阈值调整相似度的大小，有效避免了陷入局部最优，使得最终的聚类结果更理想.改进后的算法在迭代次数和半径的选择上都要优于标准蚁群聚类算法和自适应蚁群聚类算法，在聚类的速度方面得到了较大的提升.实验结果表明改进后的算法在迭代次数上更少，算法的收敛速度更快，效率更高.将改进后的算法用于客户细分，实验结果与K均值聚类算法对比分析发现，改进后的算法识别客户的正确率明显高于K均值聚类算法.

［1］高 尚，杨静宇.群智能算法及其应用［M］.北京:中国水利水电出版社，2006.

［2］Dorigo M，Maniezzo V，Colorni A.The ant system:optimization by a colony of cooperation agents［J］.IEEE Transaction Systems，Man and Cybernetics，Part B，1996，26(1):29-41.

［3］Dorigo M，Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem［J］.IEEE Transactionson Evolutionary Computations，1997，1(1):53-66.

［4］宋中山，陈建国，郑波尽.一种多项指标全提升的多目标优化演化算法［J］.中南民族大学学报:自然科学版，2011，30(3):89-93.

［5］宋佩莉，祁 飞，张 鹏.混合蚁群蜂群算法在旅行Agent问题中的应用［J］.计算机工程与应用，2012，48(36):33-38.

［6］陈庆全，张栋楠，张永平.基于蚁群算法的动态人员疏散模拟［J］.微计算机信息，2012，28(10):424-426.

［7］周 腾，基于MATLAB的自适应蚁群聚类算法研究与仿真［J］.软件，2012，33(7):105-107.

［8］张春凯，王丽君.基于遗传算法的一种改进的K-均值聚类算法［J］.计算机工程与应用，2012，48(26):144-147.

［9］Faieta B，Lumer E.Exploratory database analysis via selforganization［C］//RIAO.4th International Conference on Computer-Assisted Information Retrieval(RIAO 1994).NY:Rockefeller University，1994:570-584.

［10］Swee Chuan Tan，Kai Ming Ting，Shyh Wei Teng.Simplifying and improving ant-based clustering［C］//ICCS.Proceedings of the International Conference on Computational Science.Tsukuba:Elsevier，2011:46-55.

［11］张 蕾，曹其新，李 杰.一种基于群体智能聚类的设备性能横向比较算法［J］.上海交通大学学报，2006，40(3):439-443.

［12］周晶平，宋中山.旅行社客户关系OLAP系统的设计与实现［J］.中南民族大学学报:自然科学版，2012，31(4):101-104

［13］张建萍，刘希亚.基于聚类分析的K-means算法研究与应用［J］.计算机应用研究，2007，24(5):166-168.