湖北省CPI和PPI关系的实证分析

张利斌，刘龙飞，冯 益

(1北京大学光华管理学院，北京100084;2中南民族大学经济学院，武汉430074;3华中科技大学管理学院，武汉430074)

CPI(居民消费价格指数)和PPI(工业品出厂价格指数)是我国价格指数体系中最重要的两种价格指数，它们较好地显示了社会经济运行状态，代表了一定时期商品市场和生产要素市场中供求关系的变化情况.从供给角度，PPI的涨跌会顺着产业链传导到零售价格和服务项目上;从需求角度，CPI的涨跌也会通过市场和投资心理因素反馈给PPI.由于对CPI与PPI之间相互关系的研究结论能用于解释物价指数下降或者上升的经济现象，并能对经济未来走势进行预测，为政府制定宏观调控政策(如价格政策和居民消费政策)起到重要的指导作用.因而，在经济发展的不同时期，两者之间可能存在的多种关系也引起了理论界和实务界的广泛关注，尤其是两者的“传递”问题［1-3］.学者大多以PPI向CPI的价格传递为假定，从理论和实证角度探讨了PPI向CPI的传递效率和时滞问题.刘敏等(2005)采用1990年以来的山东省月度同比价格指数利用相关矩阵和相关系数考察了CPI与PPI及其各构成部分的相关关系，认为PPI与CPI之间具有带有明显滞后期影响的线性关系，PPI的变动在滞后一段时期后一定会影响CPI的变动［4］.贺力平(2008)采用全国2001年1月至2008年7月数据得出了不同的结论，指出，CPI是PPI的格兰杰原因，后者经过1～3个月左右的时滞对前者的变动做出反应［1］.姜义美(2006)采用全国1997年1月至2005年10月数据，指出，不同时期两者之间的传递关系不一样:自1997年以来，PPI波动4个月后对CPI影响最为显著;而从2002年11月到2005年10月的数据表明，CPI对 PPI有短期和中长期影响［5］.还有学者进行了双向检验，张延群(2007)根据全国1999年1月至2005年12月数据对消费价格指数、商品零售价格指数、原材料燃料动力购进价格指数和工业品出厂价格指数建立协整向量自回归模型，指出，从长期看，消费价格指数的走势决定商品价格指数走势;从短期看，原材料价格指数的上涨会引起消费价格指数的上涨［6］.近期的研究多采用建立VAR模型等计量方法对CPI和PPI的相互关系及其影响因素进行了探讨(方燕，尹元正，2009［7］;杨宇，陆奇岸，2009［8］)，得到了CPI与 PPI保持相互影响的正向时滞关系.

通过文献回顾，我们发现，目前研究有以下特点:第一，采用的数据大多是全国数据，样本区间并不一致;第二，现有结论缺乏一致性;第三，对行政省数据进行检验还很鲜见.虽然我国各省并不是独立的经济体系，但是，目前不少省份的经济规模已超过许多独立经济体，同时，不同省份的CPI和PPI具有较大差别.例如，通过对2001年1月至2011年12月湖北省和广东省CPI、PPI数据的比较，我们发现绝大部分时间内湖北省两个指标的数值均高过广东省.本文以湖北省为例，探究我国行政省CPI和PPI之间的传递规律.结果表明:在考察期内，湖北省的PPI与CPI互为格兰杰原因，它们两者都倾向于两个月时滞后引起对方的同方向变动，而在全国水平上，大多数研究结论都认为PPI对CPI的影响较小，即PPI与CPI的倒挂现象，因此本文的研究结果从一个侧面反映了湖北省区别于全国的经济发展特点.

1 辨析CPI与PPI

CPI主要反映消费者购买商品和服务的价格变化情况，由8项分类指标构成，由国家每5年修定一次权重进行计算.PPI主要反映工业产品在出厂时的价格变动趋势和变动程度的相对数.CPI与PPI的“商品篮子”的构成有所不同，存在重合和区别.

CPI与PPI的联系:统计范围具备重合性，即生活资料这一部分.就这部分商品而言，它们是CPI与PPI的比较直接的联系纽带，但同时也存在差别，主要在于商品计价的方式，如批发价格与零售价格，以及它们在计算时所占的权重.

CPI与PPI的区别:第一，PPI较少包含服务项目，而CPI则包括很多服务项目在内;第二，在农副产品上，PPI仅涉及进入工业加工环节的那部分，而CPI则还涉及未进入工业加工环节的农副产品;第三，PPI涉及许多其最终用途为出口的产品，即不进入国内消费市场的部分，而CPI则涉及许多进口的工业品.

因此，在客观上并不能保证CPI与PPI的变动幅度总能保持一致.本文使用2001年1月至2010年11月湖北省月度同比数据对PPI和CPI大类构成的权重进行了一个快速和近似的估算.这个快速估算基于这些产品类别权重在样本期间保持不变的假定.这里采用OLS法，依据公式CPI(PPI)βi=1(βi为各产品类别的权重，Xi为各构成项目).表1给出两个指数各构成类别的估算权重系数.

从上述估算结果可看到，湖北省PPI中生产资料和生活资料的权重分别约为75.6%和24.4%;CPI中物品和服务的权重大约分别为77.9%和22.1%.生活资料在PPI和CPI中所占的权重的差别是比较大的.

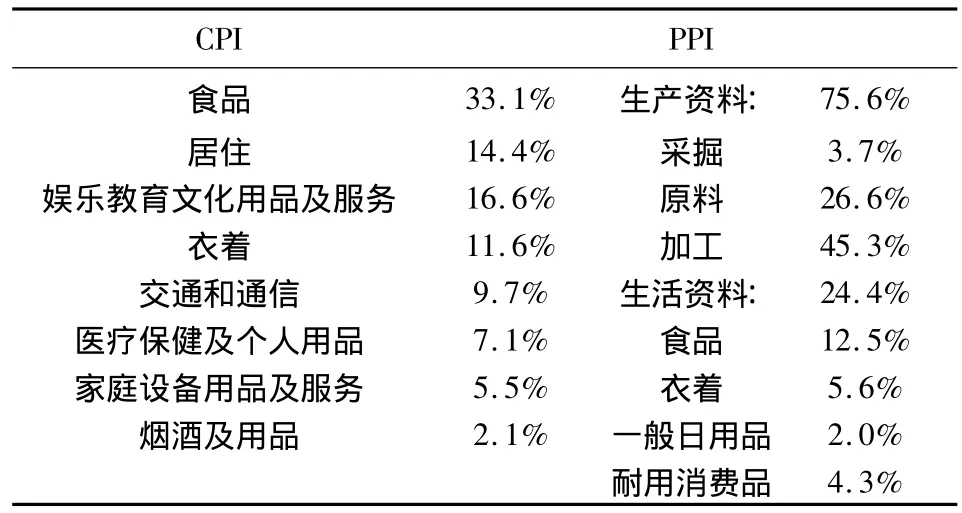
表1 CPI与PPI权重系数Tab.1 Weight coefficient of CPI and PPI

2 对湖北省CPI和PPI的格兰杰因果关系检验

格兰杰因果关系检验方法对因果关系的定义是:如果一个变量的滞后值能有效的帮助预测另一个变量，那么这个变量就是另一个变量的格兰杰原因.这意味着CPI与PPI的关系存在4种可能:(1)CPI是PPI的格兰杰原因，PPI不是CPI的格兰杰原因;(2)CPI不是PPI的格兰杰原因，PPI是CPI的格兰杰原

因;(3)CPI是PPI的格兰杰原因，PPI也是CPI的格兰杰原因，即双向格兰杰因果关系;(4)CPI不是PPI的格兰杰原因，PPI也不是CPI的格兰杰原因，即CPI和PPI之间不存在格兰杰因果关系，是相互独立的.格兰杰因果关系检验的表达式为:

在两个公式中，下标i表示时滞长度(本文使用月度数据，因此它们为滞后月度数);k表示滞后阶数;αi和βi分别是因变量滞后值和自变量滞后值的系数;μt和εt为满足统计要求的随机误差项.这是一个未设限制的检验模型，这个检验模型的原假设为:βi组整体系数为0，即:

其中i为选取的滞后数.若H0假设成立，即因变量的滞后值对自变量没有预测力，即因变量不是自变量的格兰杰原因.检验过程就是根据这个模型构建并计算F统计量的值，和F统计量的P值，然后与显著性进行比较，最后得出因果关系检验的结果.

图1 湖北省CPI与PPI走势图(数据来源:中经网)Fig.1 Trend of CPI and PPI in Hubei Province

本文采用湖北省2001年1月到2010年11月的CPI与PPI的月度数据进行计量检验，共有108个观察值，如图1所示.选取这段时期数据的原因在于:一是因为2001年以前的数据不完整，不便于数据的调整;二是从我国经济发展历史来看，由于经济体制的转变和开放政策的变化导致不同时期CPI与PPI的情况不同，所以选择相对较近时期是比较合适的.图1显示:在观察期，两者总体起伏趋势既有一定程度的类似性，但也存在着明显的差异，例如在一些年份中，出现了“剪刀差”走势，值得注意的是，从2002年底到2007年中期，以及2008年底都表现出PPI超过CPI的情况.

为了保证检验的准确程度，本文对数据进行了调整:一是调整为以2000年为基期的月度同比数据序列，使用同比数据可以在很大程度上剔除季节因素的影响;二是进行对数化处理，减少异方差性的影响，但对于经济意义分析没有影响;三是采用Census X12方法，从数据上看，在采用同比数据后仍然具有明显的季节特征，所以进一步采用了国际通用的X12方法进行季节调整.

第一步，数据序列的平稳性检验.协整检验和格兰杰因果关系检验的检验条件都要求事先进行数据的单位根检验，前者是需要保证两个数据序列具有相同的单位根个数，也称单整的阶数，后者则要求数据序列是平稳的.这里采用ADF单位根检验方法.从表2可以看到检验结果为:CPI与PPI数据的对数序列都是一阶单整的，即I(1).意味着CPI与PPI序列都是不平稳的，但单整阶数相同，所以可以进行协整检验，同时，在进行一阶差分处理后都可以达到平稳，从而可以进行格兰杰因果关系检验.

表2 ADF单位根检验结果Tab.2 Results of the ADF unit root test

第二步，协整检验.因为只有两组数据序列，所以采用E-G两步法:首先对两个变量采用OLS法进行回归估计，然后检验得到的残差序列的平稳性，如果残差序列平稳则说明存在协整关系.

协整方程表达式:

残差ε1和ε2的单位根检验结果如表2所示，在5%显著水平上都通过了检验，所以可以认为CPI与PPI之间存在协整关系.

第三步，格兰杰因果关系检验.采用Eviews6.0进行格兰杰因果关系检验结果如表3.A代表零假设:DLNPPI does not Granger Cause DLNCPI，B 代表零假设:DLNCPI does not Granger Cause DLNPPI.通过建立VAR模型获取AIC、SC和似然对数值进行检验我们可以得到1或2为最优滞后阶.

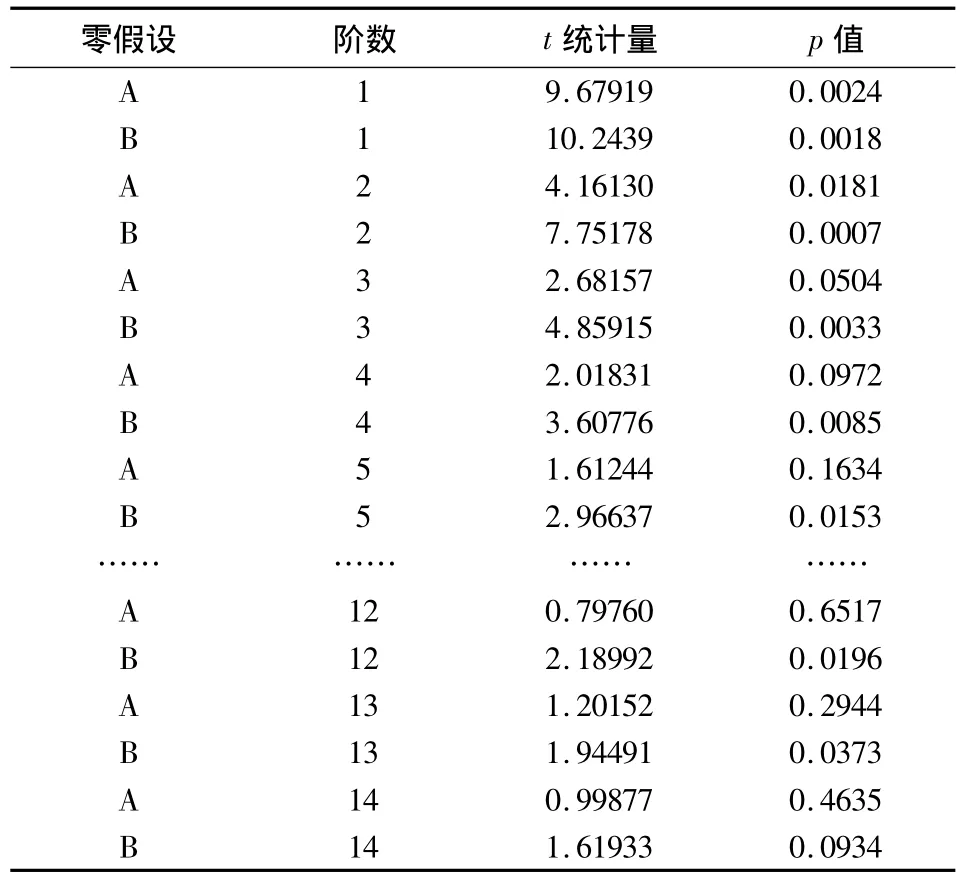
表3 格兰杰检验结果Tab.3 Results of the Granger test

综上，2001年1月到2010年11月的湖北省的CPI与PPI月度同比数据对数序列为一阶单整序列;E－G两步法检验结果表明两者存在协整关系;在考察期间，滞后1～3期的CPI和PPI互为格兰杰因果关系，互相都有预测帮助;4～13期PPI不是CPI的格兰杰原因，但CPI一直是PPI的格兰杰原因;14期之后双方互相不为格兰杰原因.

3 PPI关于CPI滞后项的二次拟合回归分析

鉴于以上分析结果，考虑到1～13期CPI一直是PPI的格兰杰原因，下面建立PPI关于CPI的函数关系.

即使PPI和CPI原数据均不是平稳序列，但经检验他们之间存在协整关系，而具有协整关系的经济变量具有长期的稳定关系，因此可以使用经典回归模型方法建立PPI和CPI滞后项的回归模型.

运用OLS回归分析的方法，讨论 PPIt关于CPIt－1，CPIt－2，CPIt－3的回归函数，考虑到CPIt－1，CPIt－2，CPIt－3可能存在多元共线性的影响，这里采用逐步回归的方法对数据进行拟合，由于 CPIt－2，CPIt－3的系数估计值均没有通过t检验，不显著，予以剔除，得到的回归结果如表4所示.

表4 回归结果Tab.4 Result of the regression

由以上回归结果分析可知，拟合优度达到0.6518;回归方程的显著性检验显示，在显著性水平α为0.05的情况下，由于概率p值近似为0，小于显著性水平α，应拒绝回归方程显著性检验的零假设，认为各回归系数不同时为零，被解释变量与解释变量全体的线性关系是显著的，可建立线性模型.而回归系数显著性t检验的概率p值均小于显著性水平α，因此应该拒绝原假设，认为回归系数显著不为零.

对 PPI和 CPIt－1，CPIt－2，CPIt－3的相关分析结果如表5所示.

表5 相关分析结果Tab.5 Result of the correlation analysis

由表5可以明显看出，PPI与CPIt－1的相关系数最大，达到0.809;而 CPIt－1，CPIt－2，CPIt－3之间也确实存在着高度的相关性，因此这也说明了 CPIt－1，CPIt－2，CPIt－3之间确实存在着多元共线性，在逐步回归的过程中将变量 CPIt－2，CPIt－3剔除出去，仅剩下变量 CPIt－1.

综上得到的回归方程为 PP∧It=－16.467+1.16CPIt－1+εi，但经对残差 εi的单位根和 QLB统计量检验发现，其是平稳的非白噪声序列，残差的自相关图呈拖尾性，而偏自相关图显示其可能是1、9、13阶截尾的，因此，我们分别采用AR(1)、AR(9)、AR(13)模型对残差结果进行分析，得到的AIC和SC值如表6所示.

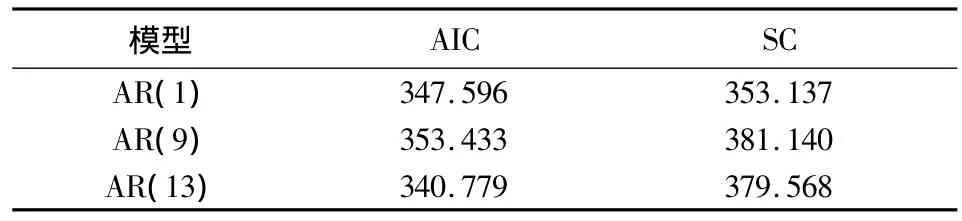
表6 AR(i)模型的AIC和SC值Tab.6 Values of AIC and SC of the model of AR(i)

根据AIC和SC越小越好的原则，这里最终选取了AR(1)模型对残差序列进行分析，得到的拟合结果为 εt=0.117+0.87εt－1+υt，υt～N(0，1.082).

检验结果显示回归模型显著成立，参数显著非零，残差序列为{υt}白噪声序列.

综合以上两个函数分析结果得到PPIt关于CPIt回归 结 果 为:PP∧It=－16.467+1.16CPIt－1+～N(0，1.082)，其中 B 为延迟算子.

利用以上方程对PPI序列进行预测得到的拟合序列图和真实序列图如图2所示.

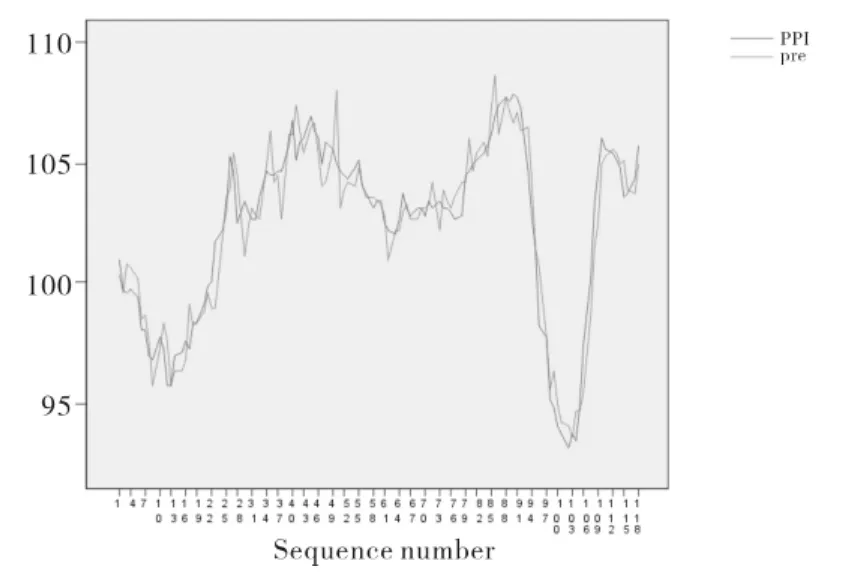
图2 PPI真实值和一元线性回归预测值的拟合图Fig.2 Fit chart of the real values of PPI and forecast values of the unary linear regression

根据图2可以看出，拟合函数对PPI的原数据具有较好的拟合效果.

由拟合函数结果可以看出PPIt关于CPIt的长期弹性为1.16，也就是说当 CPIt－1增加 1%，那么 PPIt也相应的增加1.16%，存在显著的正相关关系.

为了对模型进行验证，我们利用所得模型对2010年12月份的PPI数值进行预测，得到的预测值和真实值的比较结果如表7所示.

表7 2010年12月PPI真实值和一元线性回归预测值Tab.7 Real value of PPI in December of 2010 and forecast value of the unary linear regression

考虑到只有一个解释变量，一元线性回归分析结果的拟合优度0.6518也不是很高，而预测相对误差达到1.02%也不是很理想，因此我们尝试用一元多项式回归，结果得到PPI关于CPIt－1的回归最优多项式是二次的.因为对随机干扰项的White异方差检验结果显示，随机干扰项之间确实存在着异方差性，所以这里采用加权最小二乘法(WLS).这里的权重取，w，于是得到的拟合结果如表8所示.

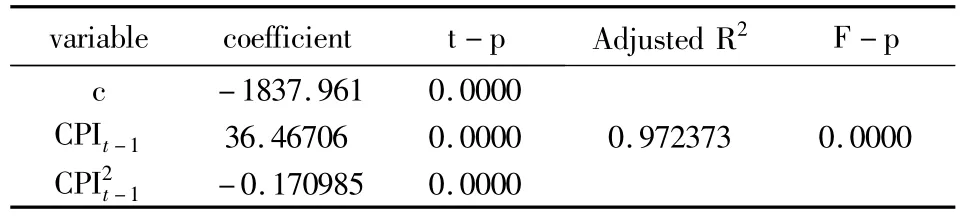
表8 一元二次回归结果Tab.8 Result of the quadratic regression

方程拟合优度达到0.97，接近于1，拟合优度较高，高于一元线性回归分析结果的拟合优度0.6518;方程整体性和各系数的显著性检验均通过检验，参数显著不为零.而采用普通最小二乘法进行一元二次多项式回归得到的回归的经过调整的拟合优度为0.765393，可见，采用加权最小二乘法对一元二次方程拟合的结果显著优于一次的和未加权的二次的拟合结果，综上得到的回归方程为:PPIt=－1837.961+36.467CPIt－1－0.171CPI2t－1+ εt经对残差 εt的单位根和QLB统计量检验发现，其是平稳的非白噪声序列，残差序列的自相关图呈拖尾性，偏自相关图显示其可能是1、13阶截尾的，因此，我们分别采用AR(1)、AR(13)模型对残差结果进行分析，得到的AIC和SC值如表9所示.

表9 AIC和SC值比较Tab.9 Comparison of the value of AIC and SC

根据AIC和SC越小越好的原则，这里最终选取了AR(1)模型对残差序列进行分析，得到的拟合结果为 εt=0.7553εt－1+υt，υt～N(0，1.3737).

检验结果显示回归模型显著成立，参数显著非零，残差序列{υt}为白噪声序列，有效剔除了异方差性和自相关性.

综合以上两个函数分析结果得到PPIt关于CPIt－1回归结果为:PPIt=－1837.961+36.467CPIt－1－+～N(0，1.3737)，其中B 为延迟算子.利用以上方程对PPI序列进行预测得到的拟合序列图和真实序列图如图3所示.

图3 PPI真实值和一元二次回归预测值的拟合图Fig.3 Fit chart of the real values of PPI and forecast values of the quadratic regression

根据图3可以看出，拟合函数对PPI的原数据具有较好的拟合效果.

为了对模型进行验证，我们利用所得模型对2010年12月份的PPI数值进行预测，得到的预测值和真实值的比较结果如表10所示.

表10 2010年12月PPI真实值和一元二次回归预测值Tab.10 Real value of PPI in December of 2010 and forecast value of the quadratic regression

由表10可以看出相对误差较小，在误差允许范围内可以接受预测的函数结果.同时，我们发现利用一元二次多项式回归得到的函数所获得的预测值比利用一元线性回归分析得到的预测值要更加接近实际值，相对误差更小，预测的准确性更高.

需要说明的是:由于滞后1到3期的CPI和PPI互为格兰杰因果关系，互相都有预测帮助，而函数关系是相互的，这里仅建立了PPI关于CPI滞后项的函数模型，而CPI关于PPI滞后项的函数模型也可以建立，限于篇幅，在此不详述.

4 对检验结果和模型的进一步说明

实证结果表明，湖北省CPI与PPI在考察期间存在着长期均衡关系和双向的格兰杰因果关系，可以利用这两个指标进行相互的预测分析，并且能够构建PPI关于CPI滞后项的回归模型用于预测.但CPI和PPI都会受到复杂多样因素的冲击，从而对这一价格传递的机制产生不同的作用，并影响到对结果的预期.比如投资需求的波动引起生产资料价格变动，从而促使PPI发生变动;而另一方面，消费需求的变化将带来商品市场价格的波动，进而导致CPI产生波动.也有实证研究探讨了货币供应增长率对CPI的影响(方燕，尹元生，2009)［7］、股票收益对 CPI和 PPI都产生了影响(陈践，梅梅，2009)［9］.政府对部分物资和商品价格的作用力较大，特别是原材料和能源价格都在政府的有效监控下，受市场机制和国际环境的影响较小，即价格没有完全放开，这对于价格的传递效率亦产生了重要的影响.全球次贷危机对我国及我省经济产生的冲击，亦可能造成对协整关系的不利影响.

5 结论

(1)湖北省PPI与CPI存在着多种密切的联系和重要的区别，从湖北省经济数据的计量检验结果来看，二者之间的确存在长期的均衡关系.PPI关于CPI滞后项的二次拟合回归分析表明，t期PPI是(t－1)期CPI的一元二次函数.它们之间存在相互影响，但同时也各自受到众多其他因素的影响.

(2)在1到3期湖北省CPI和PPI互为格兰杰原因.即CPI可以帮助预测PPI.而后者亦能对前者起到预测帮助的作用.

(3)在湖北省PPI向CPI传递的同时，CPI也在发生着向PPI的价格传递，并且在4到13期，CPI是PPI涨跌的主导因素.PPI关于CPI滞后项的二次拟合函数也较好地指出，在双向传递中，湖北省经济结构中需求方面因素发挥着显著影响.

(4)湖北省CPI与PPI的实证结论与基于全国数据的检验结果不一致.这里可能存在的原因包括:首先，湖北省虽然相对于全国并非是一个非常完整的经济体系，但从规模来说已经存在一定研究价值，这也是各个省市经济发展不一致的部分原因之所在;其次，湖北省的经济运行情况受全国经济状况影响，与其有关联，但受市场分隔的影响，也存在着差异，随着全国各地市场一体化程度的不断提高，可能会发生趋同现象.相关研究表明产生差异的是价格指数的波动幅度和个别省市运行上的领先或者滞后.

［1］贺力平，樊 纲，胡嘉妮.消费者价格指数与生产者价格指数:谁带动谁［J］.经济研究，2008(11):16-26.

［2］贺力平，樊 纲，胡嘉妮.消费者价格指数与生产者价格指数:对徐伟康商榷文章的回复意见［J］.经济研究，2010(5):149-154.

［3］徐伟康.对《消费者价格指数与生产者价格指数:谁带动谁》一文的质疑［J］.经济研究，2010(5):139-148.

［4］刘 敏，张燕丽，杨延斌.PPI与CPI关系探析［J］.统计研究，2005(2):24-27.

［5］姜义美.我国价格传导链的实证分析［J］.甘肃农业，2006(4):48.

［6］张延群.商品价格指数是消费价格指数的前导变量吗——基于二阶单整向量自回归模型的实证研究［J］.数量经济技术经济研究，2007(12):140-149.

［7］方 燕，尹元生.基于VAR模型的居民消费价格指数传导机制研究［J］.北京工商大学学报，2009(1):70-74.

［8］杨 宇，陆奇岸.CPI、RPI与 PPI之间关系的实证研究——基于VAR模型的经济计量分析［J］.价格理论与实践，2009(5):57-58.

［9］陈 践，梅 梅.股票收益与消费者价格指数、工业品出厂价格指数之间价格传导关系的研究［J］.新西部，2009(4):38-39.