单框架控制力矩陀螺构型分析与奇异可视化

魏孔明 吴忠 刘涛

（北京航空航天大学仪器科学与光电工程学院，北京100191）

1 引言

单框架控制力矩陀螺 （SGCMG）系统的构型包括两层含义，即系统中采用SGCMG的个数以及各SGCMG的空间安装形式。构型不仅决定了SGCMG系统角动量包络的大小和形状，而且还决定了奇点在空间中的分布。良好的构型不但可以充分利用SGCMG系统的力矩输出能力，而且可以降低奇点分布的复杂度，从而利于操纵律的设计。因此，构型分析与设计是SGCMG应用的基础和前提。

对于控制力矩陀螺系统构型，国内外学者从多种角度进行了研究。文献[1]针对控制力矩陀螺在空间站中的应用，考虑了质量、功率、体积、安全性、可维护性和寿命等指标，对各种典型构型进行了对比分析，给出了构型选择依据。然而，该研究主要考虑了控制力矩陀螺个数的影响，并未考虑安装形式的影响以及构型与奇异的关系。文献[2]以航天器姿态控制精度为指标，对构型参数进行了优化，使得在该构型参数下姿态控制精度最高，然而该研究同样没有考虑构型对奇异的影响。在文献[1]的基础上，文献[3]采用构型效率、奇异面复杂度作为评价指标，文献[4]则采用构型效益、可控效益、奇异点损失率和失效效益作为评价指标，对SGCMG系统的典型构型进行了对比分析。构型评价指标虽然考虑了安装形式以及构型对奇异的影响，但是数字指标不能很好地刻画不同构型下系统奇点的分布情况。

本文分析了构型效益和可控效益对构型性能描述的不足，并进行了改进，引入了两个新的构型评价指标，用于典型构型的对比与分析。同时，利用可视化方法对SGCMG系统在不同构型下的奇异角动量曲面分布情况进行了对比研究，分析了构型对系统奇点分布的影响，为构型设计提供了依据。

2 构型描述及评价指标

2.1 构型描述

为使SGCMG系统具有冗余和奇异回避能力，应采用3个以上的SGCMG。然而，当SGCMG超过6个时，系统奇异面的复杂度不会再显著降低，而且过多的SGCMG会使系统的质量及功耗随之增加。因此，本文只研究由4个、5个或6个SGCMG组成的系统。

根据各SGCMG框架轴是否重合，可将SGCMG系统构型分为：对称安装构型和成对安装构型。在对称安装构型中，各SGCMG的框架轴垂直于正多面体或正棱锥的表面，该类构型具有较好的对称性，从而使系统具有较好的失效操纵相容性。在成对安装构型中，每两个SGCMG组成一对，框架轴同向，该类构型降低了SGCMG系统奇异面的复杂度，有利于操纵律的设计。因此，本文主要针对三类构型进行分析：第一类为正棱锥构型，各SGCMG的框架轴垂直于正棱锥的各侧面；第二类为正棱锥加轴构型，一个SGCMG的框架轴垂直于正棱锥的底面，其余各SGCMG的框架轴垂直于正棱锥的各侧面；第三类为成对安装构型，每个控制轴上有一对SGCMG共轴成对安装。

设SGCMG系统由n个相同的SGCMG组成，第i个SGCMG的角动量为hi，各SGCMG角动量大小相等，均为h0。设框架轴方向上的单位向量为gi，角动量初始方向上的单位向量为ai，bi与gi和ai构成右手正交坐标。hi在ai与bi组成的平面内绕gi转动，框架角σi为hi与ai的夹角。定义A、B为SGCMG系统的构型矩阵，则SGCMG系统的运动学方程可表示为

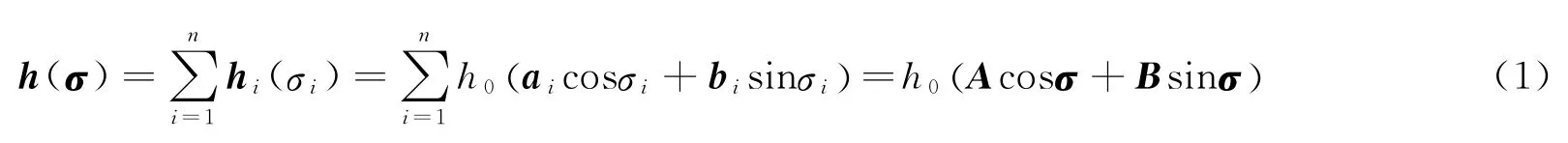
式中h为系统总角动量，σ＝ [σ1…σn]T为系统框架角组合，A＝ [a1…an]，B＝[b1…bn]，cosσ＝[cosσ1… cosσn]T，sinσ＝[sinσ1… sinσn]T。 已知系统构型矩阵，可根据式（1）方便地写出SGCMG系统的运动学方程。

2.2 构型评价指标

常用的构型评价指标包括构型效益、可控效益和失效效益等[4]，针对构型效益和可控效益的不足，在此引入角动量利用率和非奇异率，对SGCMG系统构型进行分析和评价。

（1）构型效益

构型效益是指角动量包络内切圆半径与各SGCMG角动量值代数和之比，可表示为

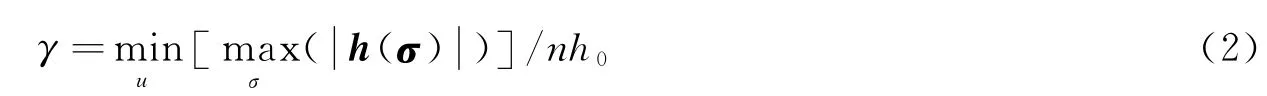
（2）可控效益

可控效益是指角动量空间中不包含椭圆奇点 （不能通过零运动脱离的奇点）的最大角动量球空间的半径与各SGCMG角动量值代数和之比，可表示为

式中σse表示系统椭圆奇点。可控效益是SGCMG系统奇点分布的一种度量，可控效益大，则不含椭圆奇点的角动量空间大，奇点分布离角动量包络近，SGCMG系统操纵律的设计也相对容易。

（3）失效效益

失效效益是指当SGCMG系统中某个SGCMG失效时系统的构型效益。失效效益反映了失效对SGCMG系统角动量包络的影响。对于对称构型，任意SGCMG失效时，失效效益相同；而对于非对称构型，不同SGCMG失效其失效效益可能不同。

（4）角动量利用率

从构型效益定义中可以看出，构型效益反映了构型对各SGCMG角动量的利用情况，构型效益越大，各SGCMG对系统角动量的贡献也越大。然而，由于SGCMG系统的特点，构型效益的最大值为γmax＝π／4，不能很好地表征构型的性能。因此，可将构型效益归一化，引入一新构型指标：角动量利用率η1。角动量利用率是归一化后的构型效益，为构型效益与最大构型效益的比值，可表示为

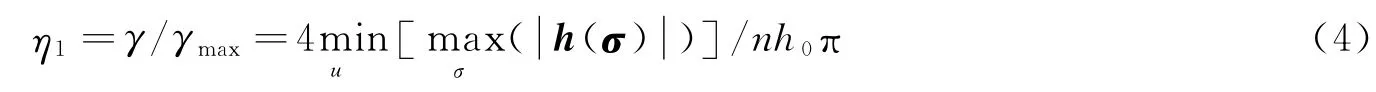
显然，角动量利用率是一个相对指标。与构型效益相比，角动量利用率能更好地反映不同构型对角动量的利用情况。

（5）非奇异率

根据可控效益的定义可知，可控效益反映了不同构型中非奇异空间的大小。由于非奇异空间中不存在严重困扰SGCMG应用的奇异问题，因此，非奇异空间的大小是衡量构型优劣的重要指标之一。然而，可控效益并没有考虑角动量包络的影响。如需比较不同构型的可控效益，应该在相同的角动量包络下比较才具有可比性。因此，可在可控效益的基础上，去除角动量包络的影响，引入一个新的构型指标：非奇异率η2。非奇异率是非奇异角动量空间半径与整个可用角动量空间半径的比值，可表示为

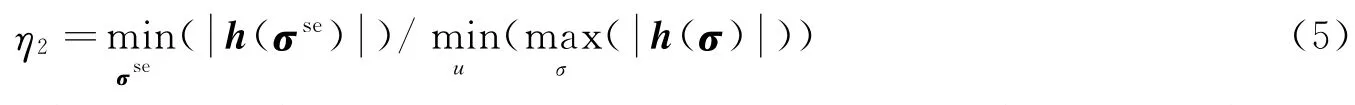
可见，非奇异率为可控效益与构型效益的比值，剔除了不同构型的构型效益对可控效益的影响，直接反映了构型对奇点分布的影响。

3 奇异可视化方法

构型评价指标虽然能够从总体上反映构型角动量包络的大小以及系统中奇点的分布情况，然而标量型的指标不能很好地反映不同构型下奇异角动量曲面在空间中分布的形态。因此，引入可视化手段[5-7]对不同构型奇异角动量曲面在空间的分布进行对比研究。

设h0＝1，则Ji＝dhi／dσi＝gi×hi为第i个SGCMG力矩输出方向上的单位向量。设SGCMG系统在u方向上奇异，当u≠±gi时，SGCMG系统的奇异角动量可表示为[5-7]

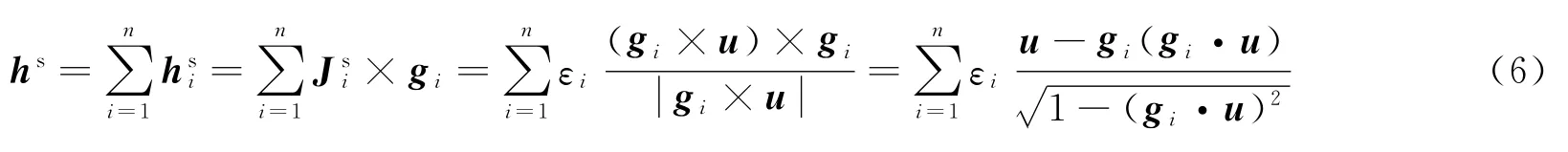
式中εi＝sign（hsi·u），上标s代表系统奇异，下同。当u＝±gi时，hi可为任意值，式（6）可改写为

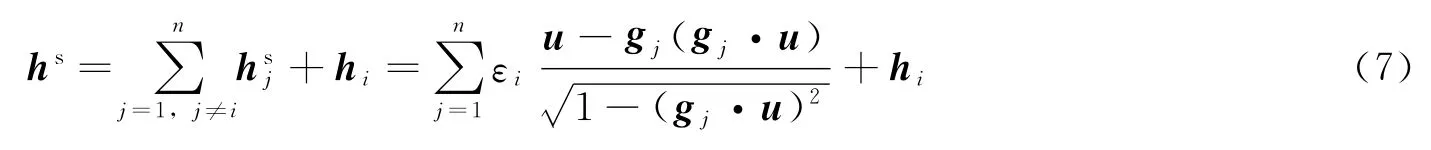
利用式（6）与式（7），根据奇异方向便可绘出指定构型的奇异角动量曲面。对于n-SGCMG系统，根据εi符号的不同，奇异角动量曲面可分为n＋型（εi全为正）、（n-1）＋型（εi为n-1正1负）等。当εi负号个数大于正号个数时，将这些符号取反后，也可归入以上类型。由文献[7]可知，对于由n个SGCMG组成的对称构型，其椭圆奇点只包含在n＋型和（n-1）＋型奇异角动量曲面上。故在以下的构型可视化分析中，只画出这两种类型的奇异角动量曲面。

4 构型分析

4.1 4-SGCMG系统构型分析

典型的4-SGCMG系统构型包括正三棱锥加轴构型、正四棱锥构型和双平行安装构型，如图1所示。为便于推导SGCMG系统的运动学关系，首先定义构型坐标系。z轴为正棱锥的体轴，x轴与棱锥的一面相对，y轴与x、z构成右手正交坐标系。

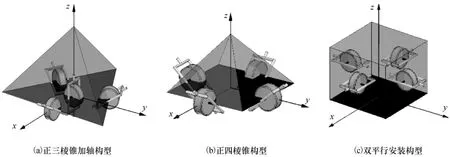
图1 4-SGCMG系统典型构型结构示意Fig.1 Sketch of typical 4-SGCMG configurations

（1）正三棱锥加轴构型

该构型中3个SGCMG的框架轴垂直于正三棱锥的3个侧面，初始角动量均沿正三棱锥的底边，以逆时针顺序排列；第4个SGCMG的框架轴垂直于正三棱锥的底面，初始角动量沿x方向。该构型的构型矩阵如下：

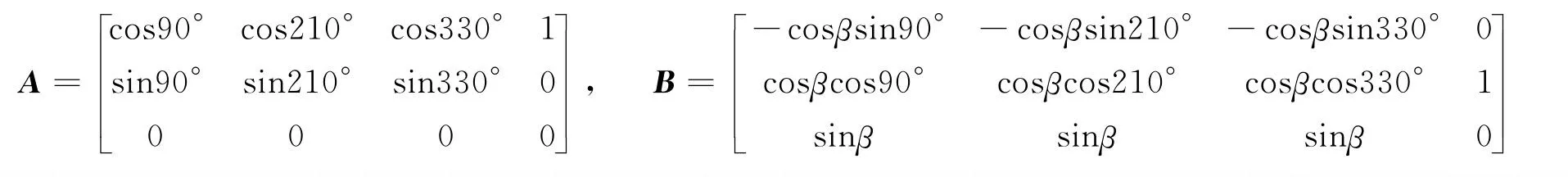
式中 构型参数β为棱锥侧面与底面的夹角。由于篇幅限制，之后的构型省略构型矩阵。当β＝arccos（1／3）时，正三棱锥为正四面体。根据构型矩阵，由式（1）可写出其运动学方程，由式（6）和式（7）可画出奇异角动量曲面如图2（a）所示。其中，外层角动量包络为4＋型奇异角动量曲面（占包络主体部分），包络中央为3＋型角动量曲面。3＋型奇异角动量曲面包含4个分支，4个分支在中心处交出一个纺锤体，该纺锤体内不含椭圆奇点，为非奇异角动量空间。设单个SGCMG的角动量为1，图2为归一化的角动量曲面，各轴的量纲为1。

（2）正四棱锥构型

正四棱锥构型又称金字塔构型 （Pyramid Type），各SGCMG的框架轴分别垂直于正四棱锥的4个侧面，初始角动量均沿正四棱锥的底边以逆时针顺序排列。当β＝arccos（／3）时，正四棱锥为正八面体的上半部分。该构型奇异角动量曲面如图2（b）所示。正四棱锥构型与正三棱锥加轴构型的奇异角动量曲面结构相似，只是空间指向不同。相对正三棱锥加轴构型，正四棱锥构型具有更多对称性，其中心非奇异空间相对较大。

（3）双平行安装构型

双平行安装构型又称为屋顶构型（Roof Type），相当于β＝90°时的正四棱锥构型。系统中两对SGCMG的框架轴共线，各框架轴分别指向x、y、-x、-y轴。初始角动量均沿正方体底边，以逆时针顺序排列。该构型奇异角动量曲面如图2（c）所示。双平行安装构型的3＋型奇异角动量曲面退化为曲线，为奇异角动量曲面随构型参数改变而变化的一种极限形式。双平行安装构型的2＋型奇异角动量曲面（图中未画出）也含椭圆奇点，不存在中心非奇异空间。但是，该构型奇异角动量曲面结构简单，有利于操纵律设计。

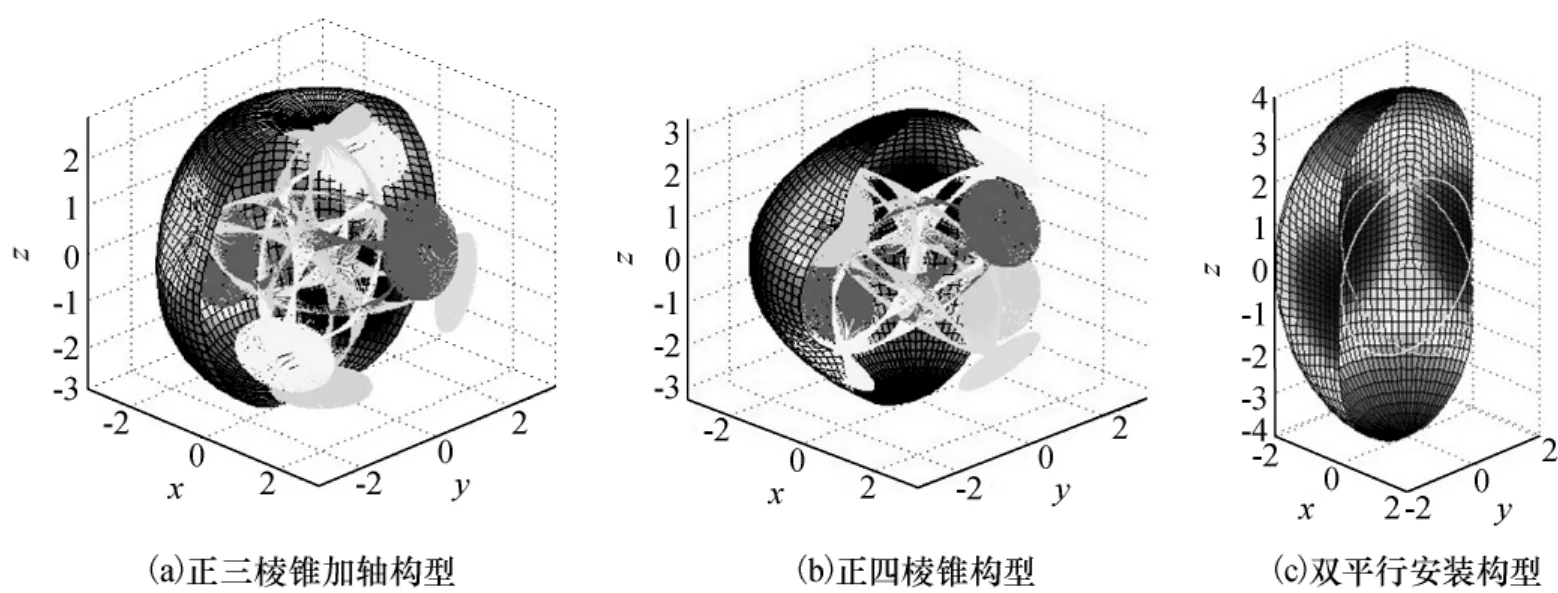
图2 4-SGCMG系统典型构型奇异角动量曲面Fig.2 Singular surface of typical 4-SGCMG configurations

（4）4-SGCMG构型指标对比

根据对三种4-SGCMG典型构型的分析，可以计算出构型评价指标如表1所示。显然，在构型效益、可控效益、失效效益和角动量利用率等指标上，正四棱锥构型明显占优。主要是由于相对于其他两种构型，正四棱锥构型对称性更好。

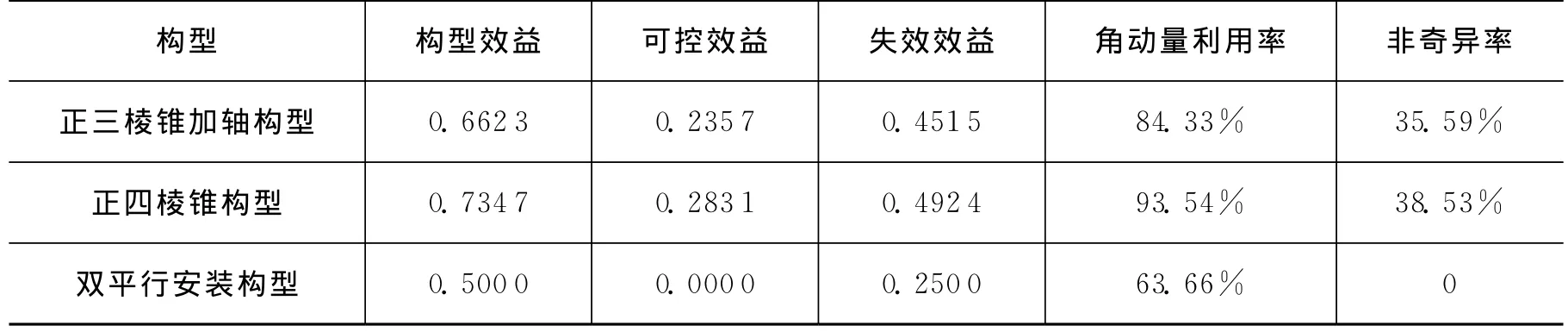
表1 4-SGCMG系统典型构型评价指标对比Tab.1 Configuration indices of typical 4-SGCMG configurations

4.2 5-SGCMG系统构型分析

典型的5-SGCMG系统构型包括正四棱锥加轴构型和正五棱锥构型，如图3所示。

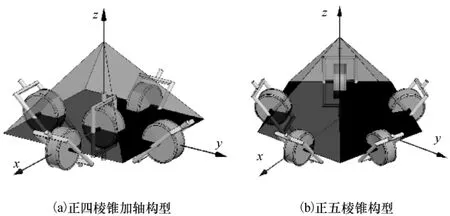
图3 5-SGCMG系统典型构型结构示意Fig.3 Sketch of typical 5-SGCMG configurations

（1）正四棱锥加轴构型

该构型中4个SGCMG的框架轴垂直于正四棱锥的四个侧面，初始角动量沿正四棱锥的底边，以逆时针顺序排列；第5个SGCMG的框架轴垂直于正四棱锥底面，初始角动量沿x方向。设构型参数，该构型奇异角动量曲面如图4（a）所示。由于4＋型奇异曲面含分支较多，不便于纸面表示，故图4（a）中只给出其角动量包络曲面。正四棱锥加轴构型的角动量包络为扁平型，与正四棱锥构型相比，其4＋型角动量曲面（图中未画出）所围成的非奇异空间占角动量空间比重较大。

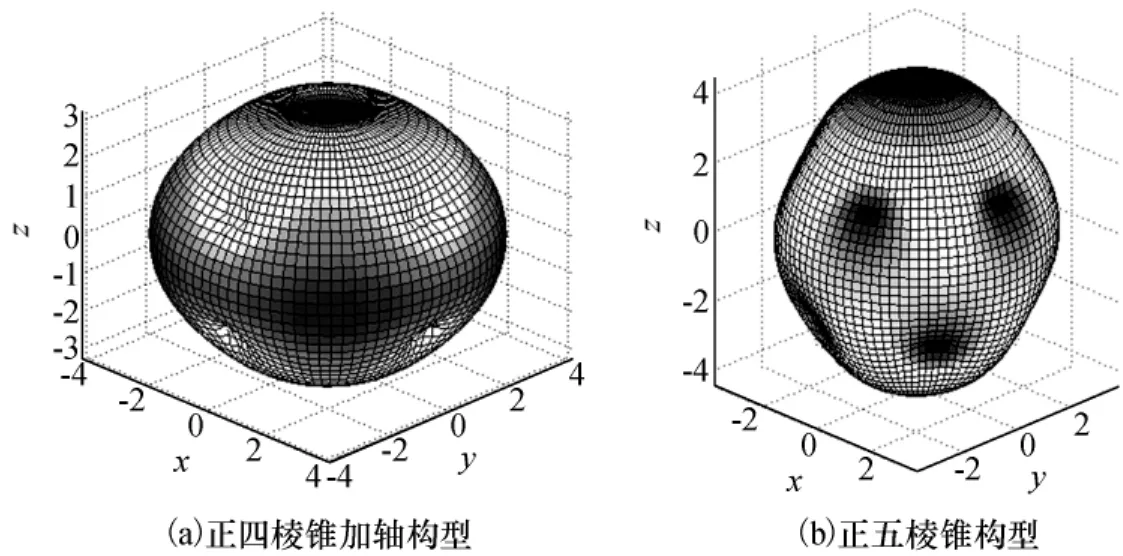
图4 5-SGCMG系统典型构型奇异角动量曲面Fig.4 Singular surface of typical 5-SGCMG configurations

（2）正五棱锥构型

该构型中5个SGCMG的框架轴均垂直于正五棱锥的5个侧面，初始角动量均沿正五棱锥的底边，以逆时针顺序排列。设构型参数该构型奇异角动量曲面如图4（b）所示。正五棱锥构型的角动量包络呈细长形，4＋型奇异角动量曲面在空间中关于z轴对称。与正四棱锥加轴构型相比，其非奇异空间也相对较大。

（3）5-SGCMG构型指标对比

根据对5-SGCMG系统典型构型的分析，可以计算出构型评价指标如表2所示。显然，在构型效益、可控效益、失效效益、角动量利用率、非奇异率等构型评价指标上，正五棱锥构型均优于正四棱锥加轴构型。从奇异角动量曲面的对比也可以看出，正五棱锥构型的奇异角动量曲面具有更多的对称性，也相对简单。与4-SGCMG系统相比，5-SGCMG系统构型评价指标全面占优。

表2 5-SGCMG系统典型构型评价指标对比Tab.2 Configuration indices of typical 5-SGCMG

4.3 6-SGCMG系统构型分析

6-SGCMG构型包括正五棱锥加轴构型、正六棱锥构型和三平行安装构型，如图5所示。

（1）正五棱锥加轴构型

该构型中5个SGCMG的框架轴垂直于正五棱锥的5个侧面，初始角动量均沿正五棱锥的底边，以逆时针顺序排列；第6个SGCMG的框架轴垂直于正五棱锥的底面，初始角动量沿x方向。构型参数）时，SGCMG各框架轴垂直于正十二面体表面，该构型奇异角动量曲面如图6（a）所示。

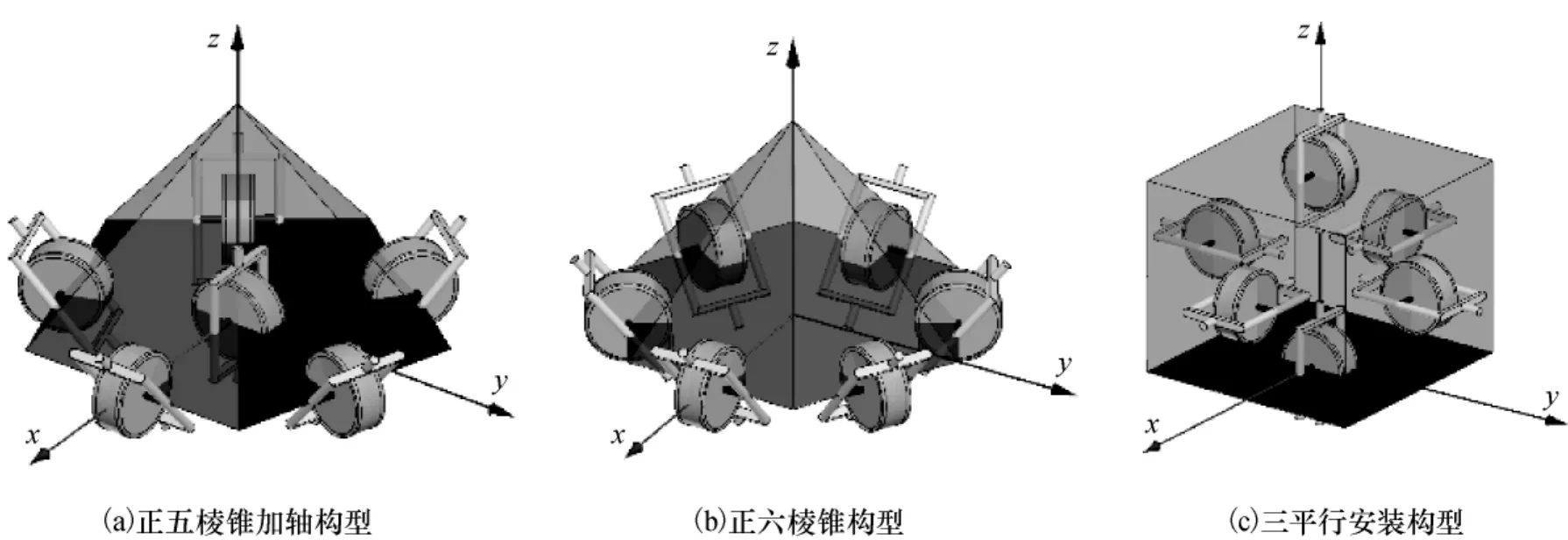
图5 6-SGCMG系统典型构型结构示意Fig.5 Sketch of typical 6-SGCMG configurations

该构型是 “和平号”空间站所采用的构型，从图6可以看出该构型不但具有较大的角动量包络，而且奇异角动量包络也接近角动量包络，是较理想的构型之一。

（2）正六棱锥构型

该构型中6个SGCMG的框架轴均垂直于正六棱锥的6个侧面，初始角动量均沿正六棱锥的底边，以逆时针顺序排列。构型参数β＝arccos（1／3）时，各SGCMG框架轴垂直于正六面体表面。该构型奇异角动量曲面如图6（b）所示。与正五棱锥加轴构型相比，正六棱锥构型的角动量包络较为细长，构型效益降低，奇异角动量曲面也相对较为复杂。

（3）三平行安装构型

该构型中，3对SGCMG的框架轴共线，各对SGCMG的框架轴分别垂直于正六面体的6个面，指向x、y、-x、-y、z、-z轴。初始角动量方向分别指向y、-x、-y、x、x、-x，该构型奇异角动量曲面如图6（c）所示。与正五棱锥加轴构型及正六棱锥构型相比，三平行安装构型的奇异角动量曲面形式相同，但其曲面结构已大为简化，5＋型奇异角动量曲面所包围的空间的形状也相对简单，其上不含椭圆奇点，为奇异角动量曲面结构随构型几何参数改变而变化的一种极限形式。

（4）6-SGCMG构型指标对比

根据对正五棱锥加轴构型、正六棱锥构型、三平行安装构型等典型构型的分析，可以计算出构型评价指标如表3所示。显然，在构型效益、可控效益、失效效益、角动量利用率等指标上，正五棱锥加轴构型明显占优。如果仅考虑构型的非奇异率，三平行安装构型则明显占优，其奇异角动量曲面分布较为简单，不存在不可回避的椭圆奇点。

表3 6-SGCMG系统典型构型评价指标对比Tab.3 Configuration indices of typical 6-SGCMG

5 结束语

本文综合运用构型效益、可控效益、失效效益、角动量利用率和非奇异率等构型指标以及奇异可视化手段对典型SGCMG系统构型进行了对比分析，具体结论如下：

1）随着SGCMG个数的增多，奇异角动量曲面结构趋于简单，不含椭圆奇点的中心非奇异角动量空间逐渐增大。

2）构型的对称性越好 （如正三棱锥加轴构型、正四棱锥构型、正五棱锥加轴构型和三平行安装构型等正多面体构型），角动量包络对称性越好，不含椭圆奇点的角动量空间越大，构型效益、可控效益、失效效益、角动量利用率和非奇异率等构型指标占优。

3）与其他构型相比，成对安装构型的构型效益较小，但其奇异角动量曲面结构较为简单，便于操纵律的设计。

[1]MEFFE M.Control Moment Gyroscope Configurations for the Space Station [C].11th AAS Guidance and Control Conference，Keystone，Colorado，USA，AAS 88-040，1988.

[2]LEVE FREDERICK A，BOYARKO GEORGE A，FITZ-COY NORMAN G.Optimization in Choosing Gimbal Axis Orientations of a CMG Attitude Control System [C].AIAA Unmanned Unlimited Conference.Seattle，Washington，USA，AIAA 2009-1836，2009.

[3]吴忠，吴宏鑫.单框架控制力矩陀螺系统的构形分析 [J].航天控制，1998（1）：19-27.WU ZHONG，WU HONGXIN.Configuration Analysis of Single Gimbal Control Moment Gyroscope Systems[J].Aerospace Control，1998（1）：19-27.

[4]张锦江.单框架控制力矩陀螺系统的构型分析和对比研究 [J].中国空间科学技术，2003，23（3）：52-56.ZHANG JINJIANG.Research on Configuration Analysis and Comparison of SGCMG System [J].Chinese Space Science and Technology，2003，23（3）：52-56.

[5]MARGULIES G，AUBRUN J N.Geometric Theory of Single Gimbal-Control Moment Gyro Systems [J].Journal of Astronautical Sciences，1978，26（2）：159-191.

[6]WIE B.Singularity Analysis and Visualization of Single-Gimbal Control Moment Gyro Systems [J].Journal of Guidance，Control，and Dynamics，2004，27（2）：271-282.

[7]TANG LIANG，XU SHIJIE.Geometric Analysis of Singularity for Single-Gimbal Control Moment Gyro Systems[J].Chinese Journal of Aeronautics，2005，18（4）：295-303.