空间机械臂系统总体技术指标确定方法

徐文福 杜晓东 王成疆 梁斌

（1哈尔滨工业大学深圳研究生院，深圳518055）（2深圳市数字化制造技术重点实验室，深圳518055）（3深圳航天东方红海特卫星有限公司，深圳518057）

1 引言

卫星由于故障、完全失效或任务结束而被放弃后，停留在空间将成为太空垃圾，不但占用了宝贵的轨道资源，还可能危及其他航天器的安全。因此，为了尽可能挽回由于卫星故障或失效造成的损失，并有效保护轨道资源，各国正在研究以卫星维修、生命延长及轨道垃圾清除为目的的在轨服务技术[1-2]。这些技术将能为未来的卫星延长5年、10年甚至15年的服务寿命[3]，空间机器人在其中将大有用武之地。总体设计是航天器系统（包括空间机器人）研制的顶层设计，即根据用户的特定任务要求，对航天器系统的功能和总体技术指标进行综合论证。为研制出满足任务需求、性能指标合理、实施方案优化的空间机器人系统，必须从系统工程的角度出发，开展总体方案的设计与仿真验证。文献[4]分析了空间机械臂与基座姿态协调控制中的关键指标，文献[3]根据轨道快车的飞行试验结果对航天器在轨捕获的任务及所达到的性能进行分析，文献[5]对用于非合作在轨服务的FREND系统的性能进行总结和评估。近年来，中国的空间机器人技术也取得了可喜的进展，文献[6]针对EMR系统进行了工作空间分析、自主规划方案设计等研究，文献[7]提出了一套小型智能飞行机器人系统的总体方案。纵观国内外的公开文献，仅有从子系统或部件角度开展的指标分析，在从系统角度开展的关键技术指标分析和论证方面，尚未形成系统的方法。本文从总体任务目标出发，结合相关的约束条件，对空间机器人系统的关键技术指标进行论证（包括机械臂的长度、末端位姿精度、末端运动速度、关节驱动力矩等），并建立动力学仿真模型，进行总体方案的仿真验证。

2 空间机械臂总体技术指标的确定

空间机器人总体方案的设计是一个反复迭代的过程，包括 “正向递推”和 “逆向迭代”过程。“逆向迭代”指当判断条件不为真时，返回对各影响判断条件的相关因素进行调整，直到该判断条件成立为止；对于无论如何调整均无法满足相关条件的情况，则需要修改任务目标或总体约束条件，即对上一级总体提出反要求。逆向迭代需要进行初步动力学仿真分析，详见后续内容。总体方案论证过程的输入为：1）总体任务目标，即对机械臂需要执行的任务、操作的对象、工作时间等提出总的要求。2）总体约束条件，包括：系统质量及功耗约束、基座姿态及轨道控制能力、结构基频要求，以及技术可实现性。而输出为机械臂系统的总体技术指标包括：机械臂长度、末端运动速度、末端位姿精度和关节驱动力矩。根据这些总体技术指标，即可开展空间机械臂的技术方案设计。

2.1 机械臂长度的确定

由于机械臂末端需要执行3D空间的位置、姿态跟踪控制，要求机械臂至少具有6个自由度（6-DOF），再考虑到奇异处理、障碍回避、关节受力优化、冗余备份等需求，因此，最好采用7-DOF冗余机械臂。对于各关节的配置，可采用在工作空间、灵巧度、奇异回避、运动学等方面具有综合性最优的S-R-S构型[8]，该构型由3-DOF的肩部、1-DOF肘部和3-DOF的腕部组成，其中肩部和腕部的3个关节轴线交于一点，等价于球关节，如图1所示。这种构型的逆运动学非常简单，适合于实时控制[9]，特别是对于空间应用，在星载机计算能力有限的条件下，采用此种臂型更显其优势。

机械臂的长度主要由机械臂工作时的操作范围决定，同时需要考虑机械臂结构基频满足总体提出的要求。图2所示为在轨执行任务时的臂型 （标称捕获状态），其中S、E、W分别表示肩部（前3个关节轴交点）、肘部、腕部 （后3个关节轴交点）。

图1 冗余机械臂最优关节配置Fig.1 Optimal joint arrangement of redundant manipulator

图2 空间机器人在轨操作示意Fig.2 Schematic diagram of space robot for on-orbit operation

由图2可知，机械臂的工作空间主要由臂杆l1和l2决定。因此，给定机械臂末端的操作范围，可初步设计两个臂杆的长度。以图2所示的标称捕获状态为例，此时机械臂肩部到腕部的位置矢量为 （Lx，Ly），两臂杆之间的夹角为θ，如图3所示，则有如下关系：

对于初步分析，为简单计，假定L1＝L2＝L／2，θ1＝θ2＝θ／2，则根据（Lx，Ly）以及θ，可计算机械臂杆件的长度。（Lx，Ly）由总体要求的操作范围确定，而θ的确定，至少需要考虑如下4个因素：1）远离肘部关节的奇异位置；2）机械臂关节处于受力比较中等的位置，即操作灵巧性较好；3）在肘部关节限位范围内，且离限位位置至少有30°的距离；4）尽可能使机械臂的工作空间较大。

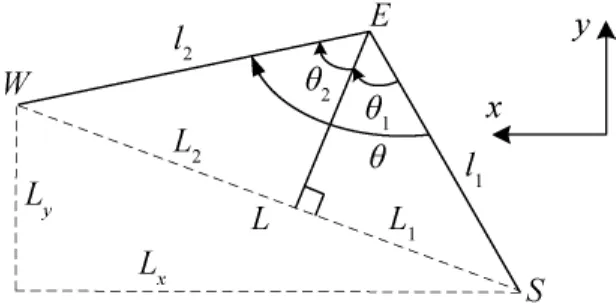
图3 机械臂杆件长度简化分析示意Fig.3 Schematic diagram for simplified analysis of the link length

上述条件为定性分析的指导性条件。以S-R-S构型的冗余机械臂为例，肘关节奇异位置为θ4＝0°和θ4＝180°[10]，相应的两臂杆夹角θ＝180°和θ＝0°；而灵巧性方面，一般认为45°和135°附近的受力条件较好。假设肘关节的运动范围为-180°～180°，则可根据θ的取值将机械臂的工作状态（在肩、肘、腕组成的平面内）表示为图4所示的情况，其中W45、W90、W135等分别表示θ＝45°、90°、135°时腕部的位置。另外，从满足抓捕条件的角度考虑，机械臂标称操作位置应该在图4中的第Ⅱ和第Ⅲ象限。综合上述4个条件，臂杆夹角在θ∈ [120°，150°]为宜，而θ＝135°为该范围的中间值。设机械臂标称操作时的条件为：Lx＝1.5m，Ly＝1m，则可求得由于机械臂肩部离其安装位置的距离为d1、腕部到机械臂末端的距离为d7，则机械臂的长度为larm＝d1＋l1＋l2＋d7，其中，d1和d7的长度分别由安装条件、球关节运动范围、末端工具尺寸等因素综合确定，若取d1＝d7＝0.5m，则larm＝d1＋l1＋l2＋d7＝2× （0.5＋0.975 7）＝2.951 3≈3m。最后设计的机械臂各部分长度为（其中l1、l2分别与图1中的d3、d5对应）d1＝d7＝0.5m，d3＝d5＝1m。

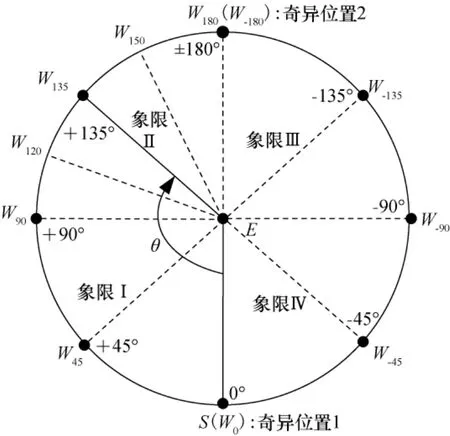
图4 机械臂两杆件夹角分区Fig.4 Partition of the angle between the two links

2.2 机械臂末端位姿精度的确定

机器人末端误差源[11]主要包括：1）关节变量Δθi引起的误差，占90%，产生Δθi的因素包括关节零位偏置、位置传感器检测误差、闭环控制误差等；2）结构参数偏差（Δdi，Δai，Δαi等），以及相邻杆件间的不垂直度或不平行度等引起的误差，占0.5%～1%；3）传动机构间隙、回差引起的误差，占0.5%～1%；4）关节及连杆柔性引起的误差，占8%～10%。

图5 机械臂末端位姿精度简化分析模型Fig.5 Simplified model for analyzing the pose accuracy of manipulator′s end-effector

由于关节变量Δθi所引起的末端误差占整个误差的90%，因此，在此主要分析Δθi产生的误差，再加上一定的裕度，可作为末端位姿误差的设计值。以如

图1所示的S-R-S臂型为例，其位置误差最大（单轴）出现在关节2、4、6或关节1、4、6同时往正向或反向均有偏差时，如图5所示。

根据几何关系可知，末端位置偏差在图5中所示坐标下可表示为

假设每个关节角的偏差为0.1°，即Δθ1＝Δθ2＝…＝Δθ7＝0.1°，代入式（2），有：

类似地，分析关节1、4、6同时往一侧有偏差时，产生的单轴最大误差也为7.9mm。由此可认为机械臂末端单轴最大位置误差为Δpm＝7.9mm，绝对定位精度

机械臂末端单轴最大姿态误差发生在4个横滚关节 （即关节1、3、5、7）同时产生同一方向偏差的情况，因此，最大姿态误差

若考虑到机械臂关节偏差引起的误差占90%，则最后得出该机械臂的末端绝对位姿精度为

2.3 机械臂末端运动速度的确定

空间机器人运动过程中，会对基座产生干扰力和力矩，导致基座姿态发生变化，机器人运动产生的干扰作用远大于航天器所受的环境干扰[12]，对基座姿态产生的影响更大。假设采用DFH-4平台作为空间机器人基座，其质量、惯量及质心位置（根据质量5t、主体几何尺寸2.36m×2.1m×3.6m，按均匀质量分布进行估计）分别为m0＝5t，r0＝ [0， 0，1.8]Tm，I0＝ diag[7237.5，7220.7，4158.2]kg·m2，作为姿态控制执行机构的某型飞轮的最大角动量为25N·ms，最大转速4 600r／min，最大输出力矩0.1Nm。

采用如图6所示的简化模型进行机械臂末端运动速度的分析。设机械臂抓持载荷以vt的速度沿X轴向运动，则产生的绕基座质心的动量矩为

式中mt为载荷的质量，vt为载荷的运动速度，（r1＋r2）为基座质心到载荷质心的距离。需要说明的是，在式（5）中，未把机械臂部分的质量包含进去，这可通过选择安全系数来保证计算的有效性。

为使机械臂运动过程中产生的最大动量矩不超过飞轮的最大角动量，需满足：

式中hRW为飞轮的最大角动量；r≥1为安全系数。根据式（5）和式（6），机械臂末端最大运动速度为

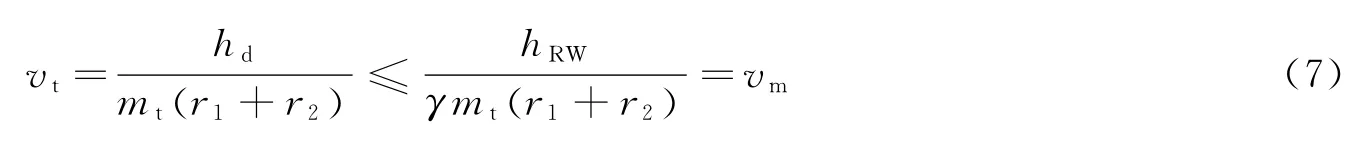
可见，末端最大运动速度vm与所携带的载荷质量mt成反比。取安全系数γ＝1.5，将上述数据代入式（7）后计算得到不同质量载荷下机械臂末端的最大运动速度，如表1所示。在同等载荷情况下，要提高末端运动速度，必须要提高基座的姿态控制能力，如采用大动量的反作用飞轮，或控制力矩陀螺CMG等。需要指出的是，在机械臂操作的过程中，要尽可能减少喷气的使用（飞轮卸载除外），这不但会消耗宝贵的控制燃料，还极易激起挠性附件（包括机械臂、基座帆板及目标航天器太阳翼）的振动。

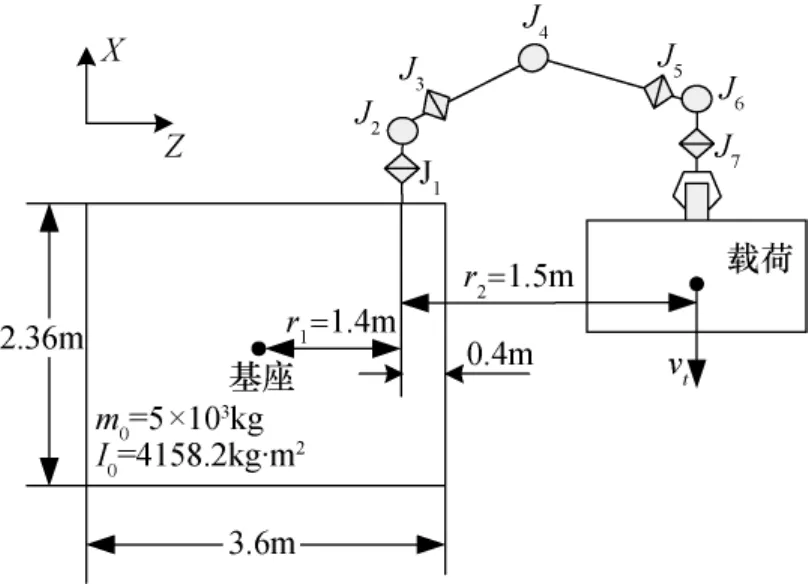
图6 空间机械臂末端运动速度分析Fig.6 Analysis of the manipulator′s end-effector velocities

2.4 关节驱动力矩确定

当负载质量特性、基座质量特性等确定后，关节驱动力矩主要由总体要求的最大加速度决定，该最大加速度表征了机械臂加、减速过程的响应速度。

如图6所示，在机械臂操作负载的过程中，根部关节（即关节1）所需要带动的负载最大，其输出的力矩也最大。设总体要求的机械臂最大关节角加速度表示为m，则关节1的最大驱动力矩为

式中Ⅰeq为关节1负载的等效转动惯量。取m＝0.05（°）／s2，安全系数γ＝1.5，则不同负载要求下机械臂关节驱动力矩如表1所示。

表1 空间机械臂总体指标要求Tab.1 Overall performance index of the space manipulator

2.5 空间机械臂总体技术指标汇总

经过上述论证，可初步得出空间机械臂的总体技术指标要求，其中，关节末端速度、关节驱动力矩等与负载的质量相关。这些总体指标如表1所示。有了这些数据后，可进一步细化机械臂关节（含电机、传动机构、传感器、轴承等）、臂杆 （材料、尺寸等）、控制器等子系统方案，从而得出机械臂的总质量、功耗等。

3 仿真研究

3.1 多种工况的仿真

通过上述方法确定空间机器人的总体技术后，可开展技术方案的初步设计，然后结合动力学仿真进一步确定所提的指标是否满足任务要求，并评估机械臂运动过程中对基座产生的干扰。假定空间机器人的基座为DFH-4平台，质量为5 000kg，操作载荷为500kg，7-DOF机械臂总质量为150kg（其中每个关节质量为18kg，每根杆件质量均为12kg），按均匀质量估计（关节质量分别分配到与其相邻的两个连杆）各刚体质量特性。根据这些参数，利用Adams建立空间机器人系统的多体动力学模型，基于此模型可开展空间机器人在轨操作过程的动力学仿真。

从扰动大小的角度来看，机械臂抓持载荷运动过程中产生的干扰最大，因此设计如下工况：1）带载常规操作工况：空间机械臂末端抓持目标，初始处于标称抓捕位置，关节1转动90°。2）带载极限操作工况Ⅰ：空间机械臂末端抓持目标，初始处于完全伸直位置，关节1转动90°。3）带载极限操作工况Ⅱ：空间机械臂末端抓持目标，初始处于完全伸直位置，关节2转动90°。该工况与工况Ⅱ的初始条件比，实际为关节1已转动了-90°，用于研究机械臂操作载荷过程中对基座最小惯量轴产生的扰动情况。

采用五次多项式规划机械臂的轨迹。仿真中基座处于自由漂浮状态，即基座姿态、质心位置均不受控，据此分析机械臂运动对基座的纯扰动。为了比较不同运动速度产生的影响情况，分别进行了运动时间tf为100s和200s两种情况下的动力学仿真。各种工况的仿真结果如表2所示。限于篇幅，工况Ⅱ的数据未给出。

表2 各种工况仿真结果汇总Tab.2 Simulation results of each case

3.2 仿真结果分析

对仿真结果进一步分析，可以得出：

1）对同一种工况来说，运动时间越长，产生的干扰力、干扰力矩越小，若时间增长为原来的2倍，则产生的干扰力、力矩大约减小为原来的1／4，即机械臂运动产生的对基座的干扰 （力、力矩）与时间平方成反比。实际上，利用多项式极值求解方法计算，可得加速度最大值对应的时刻为为例），正向及反向最大加速度为

2）极限工况Ⅰ下，机械臂运动对基座产生的干扰力和干扰力矩最大，100s运动过程中分别为0.756N（三轴合成，绝对值）和32.286Nm（三轴合成，绝对值），200s运动过程中分别为0.189 1N和0.571 5Nm。

3）自由漂浮模式下，极限工况Ⅱ的基座姿态和质心位置变化最大，其中姿态变化为[-5.42°，-4.43°，39.04°]，质心变化为[-0.165m，0.035m，-0.033m]，即姿态最大绕Z轴旋转了39°左右，质心位置沿-X轴运动了165mm左右。与极限工况Ⅰ相比，虽然所受干扰力和干扰力矩并非最大，但由于Z轴转动惯量最小，因此，姿态变化比极限工况Ⅰ下的还大 （极限工况Ⅰ主要引起Y轴姿态的变化，而Ⅰyy＝7 720.7；极限工况Ⅱ主要引起Z轴姿态变化，Ⅰzz＝4 158.2）。

4）由仿真结果可知，运动过程中机械臂的最大干扰力矩超出了飞轮控制力矩（0.1Nm），不足以满足整个操作过程中（对运动时间分别为100s和200s的情况）始终保证基座姿态稳定在期望值。针对这种情况，有3种解决方法：一是选用控制能力更强的飞轮；二是结合推进系统进行飞轮／喷气混合控制；三是拉长运动时间，减小关节最大角加速度。由于空间机械臂关节一般具有低速爬行特性，所以不可能无限制拉长运动时间，因此，应重点考虑前两种解决方案。

4 结束语

本文从总体任务目标出发，开展了空间机械臂系统总体技术指标论证，并建立动力学模型，对常规工况、极限工况Ⅰ和极限工况Ⅱ等条件下机械臂的操作过程开展动力学仿真。研究结果表明：

1）总体方案论证是反复迭代的过程，首先根据总体任务目标及约束条件开展初步设计，然后开展动力学仿真，重点分析机械臂运动所产生的对基座的干扰力和力矩，由此判断是否需要调整相关指标，并有可能对上一级总体提出反要求。

2）仿真工况的设计应兼顾常规操作和极限操作过程，其中，极限工况必须包括绕基座最小惯量轴运动的情况。

3）大范围运动下，基座姿态及质心位置变化过大 （特别是姿态，上述仿真表明极限工况下姿态偏转了40°），不利于空间机器人系统的安全运行，因此有必要采用使基座姿态扰动最小化的轨迹规划与控制方法。

4）机械臂运动过程产生的干扰力和干扰力矩的大小与机械臂运动时间成反比，所以对于干扰力和干扰力矩超标的情况，可首先考虑拉长运动时间的方案以减小干扰力和干扰力矩，但同时要兼顾机械臂的低速运动性能，不能无限拉长运动时间。此时需要考虑采用更大控制能力的飞轮，或结合喷气进行姿态控制。

[1]田富洋，吴洪涛，赵大旭，等.在轨空间机器人参数辨识研究 [J].中国空间科学技术，2010，30（1）：10-17.TIAN FUYANG，WU HONGTAO，ZHAO DAXU，et al.Parameter Identification of Orbital Free-floating Space Robot[J].Chinese Space Science and Technology，2010，30（1）：10-17.

[2]王昊瀛，王景，吴宏鑫，等.空间机器人的目标捕获自适应控制 [J].中国空间科学技术，2000，20（5）：1-9.WANG HAOYING，WANG JING，WU HONGXIN，et al.Object Capture Adaptive Control for Space Robot[J].Chinese Space Science and Technology，2000，20（5）：1-9.

[3]FRIEND R B.Orbital Express Program Summary and Mission Overview [C].SPIE，Sensors and Systems for Space Applications II，2008：1-11.

[4]ODA M.Motion Control of the Satellite Mounted Robot Arm Which Assures Satellite Attitude Stability [J].Acta Astronautica，1997，41（11）：739-750.

[5]DEBUS T J，DOUGHERTY S P.Overview and Performance of the Front-End Robotics Enabling Near-Term Demonstration （FREND）Robotic Arm [C].AIAA Infotech Aerospace Conference，Seattle，Washington，AIAA2009-1870，2009：1-12.

[6]黄献龙，梁斌，陈建新.EMR系统机器人自主规划技术的研究 [J].中国空间科学技术，2001，21（3）：6-11.HUANG XIANLONG，LIANG BIN，CHEN JIANXIN.Study on Automatic Planning Technology of EMR System Robot[J].Chinese Space Science and Technology，2001，21（3）：6-11.

[7]LIANG B，LI C，XUE L J，QIANG W Y.A Chinese Small Intelligent Space Robotic System for On-Orbit Servicing [C].IEEE／RSJ International Conference on Intelligent Robots and Systems，Beijing，2006：4603-4607.

[8]HOLLERBACH J M.Optimum Kinematic Design for a Seven Degree of Freedom Manipulator [C].The Second International Symposium on Robotics Research，1985：215-222.

[9]SHIMIZU M，KAKUYA H，YOON W，et al.Analytical Inverse Kinematic Computation for 7-DOF Redundant Manipulators With Joint Limits and Its Application to Redundancy Resolution [J].IEEE Transactions on Robotics，2008，24（5）：1131-1142.

[10]BOUDREAU R，PODHORODESKI R P.Singularity Analysis of a Kinematically Simple Class of 7-jointed Revolute Manipulators[J].Transactions of the Canadian Society for Mechanical Engineering，2010，34（1）：105-117.

[11]JUDD R P，KNASINSKI A B.A Technique to Calibrate Industrial Robots with Experimental Verification [J].IEEE Transactions on Robotics and Automation，1990，6（1）：20-30.

[12]ODA M，OHKAMI Y.Coordination Control of Spacecraft Attitude and Space Manipulators [J].Control Engineering Practice，1997，5（1）：11-21.