基于BP 神经网络的深水自升式海洋平台智能控制模型试验研究

嵇春艳，刘 聪

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

在海洋油气开发中，自升式海洋平台是目前使用最广泛的移动式钻井平台［1］。随着海洋油气资源开发的深水化，自升式海洋平台的应用水深将超过120 m，在我国南黄海、东海以及南海大陆架，需要作业水深大于150 m 的自升式钻井平台［2］。因此，自升式海洋平台的深水化发展已成为一种趋势。然而，深水自升式海洋平台的结构特点决定了其柔性较大，加之深水区域的作业环境恶劣，导致平台结构振动响应十分明显，这种过大的结构振动响应会引起结构严重的基础破坏或者整体破坏。已有研究表明，工作水深90 m 的自升式平台在波浪周期10 s，有义波高12 m 的随机波浪作用下其结构最大振动幅度可达1.5 m［3］。因此，深水自升式海洋平台的振动控制问题正日益受到关注。

目前，已有部分学者对海洋平台振动控制技术进行了相关研究，并得到了一定的研究成果。何晓宇，李宏男对安装有TLCD 的导管架海洋平台进行了振动控制分析，研究了不同大小和方向的波浪载荷对TLCD的参数优化和减震效果的影响［4］;赵东等利用扩展调谐质量阻尼器(ETMD)控制系统对导管架平台的振动响应进行了有效的控制［5］，并且对一缩尺比为1∶10 的导管架平台模型的控制效果进行了数值仿真，为后续的海洋平台相似模型振动控制实验的参数选取提供了可参考的最优区间［6］;DENG，ZHANG 利用磁流变阻尼器控制海洋结构物在冲击载荷作用下的动力响应，并进行了模型试验［7］;欧进萍，杨飏，张纪刚等研究了主动质量驱动控制系统和磁流变阻尼隔震层对典型导管架平台在地震和冰激作用下的减振效果，并进行了数值模拟与相应的振动台试验研究［8-10］;嵇春艳等对固定式导管架平台的振动控制问题进行了较多的研究工作，主要开展了半主动控制、磁流变阻尼器、模糊控制理论等方面的研究工作，并通过水池模型试验进行了验证［12，13］。综上所述，目前关于海洋平台振动控制技术的研究成果主要集中在固定式导管架平台结构的控制方法和控制技术方面，许多技术仍停留在理论研究与数值模拟阶段，缺乏模型试验验证，且在现有的平台模型试验中大多数为通过振动台和振动器提供外界激励的岸上试验，水池试验较少，更鲜见针对自升式海洋平台开展的振动控制研究工作。由于自升式海洋平台的底部固定方式、结构形式以及振动响应特点较导管架平台均存在较大的差别，因此如何设计出有效的控制系统、如何通过水池模型试验验证控制系统有效性的试验技术都是值得深入研究的问题。

本文以墨西哥湾海域某典型深水自升式海洋平台为原型，设计制作了海洋平台模型。基于BP 神经网络、以磁流变阻尼器为控制装置设计了智能控制系统，并在波浪水池中分多种工况对控制系统的减振效果进行了模型试验研究与验证。

1 基于BP 神经网络的智能控制方法

传统的主动控制算法计算出的最优控制力U(t)最精确，控制效果最好，但是它们的计算依赖于十分精确的结构振动模型，在实际控制中，当外界荷载或模型参数发生微量变化时，控制效果会受到严重影响，因此不具有鲁棒性能，同时，在实际应用中需要实时收集大量结构模型信息，而过多的信息采集和处理会产生严重的时滞现象，可行性差。神经网络具有良好的非线性映射能力，采用主动控制算法充分训练后的神经网络，既能充分继承主动控制算法控制效果的精确性，又能降低控制效果对精确结构振动模型以及外界环境输入精确程度的依赖性，可以产生很好的控制效果。

本文选用LQR 最优控制算法对一BP 神经网络进行训练，利用训练后的BP 神经网络进行智能控制。具体方法如下:

1.1 振动控制方程及最优控制力计算

在控制力作用下，深水自升式海洋平台受控结构系统可以用如下状态方程描述:

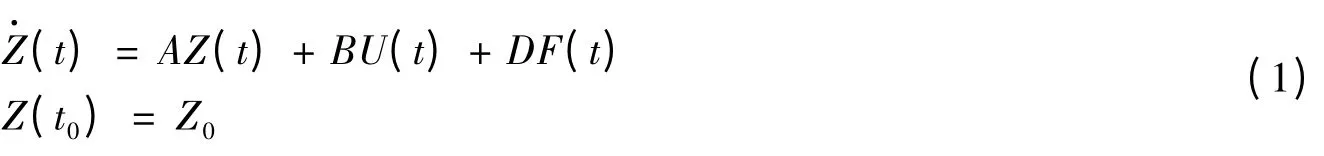
式中:

根据式(1)，按照线性二次型最优控制算法［14］计算出平台在对应于极端随机波浪载荷的试验工况下每一时刻的动力响应和相应的主动最优控制力U(t)。

1.2 BP 神经网络训练

BP 神经网络是一种单向传播的多层前向网络，由输入层、隐含层和输出层组成。该神经网络采用误差逆传播算法，即BP 算法，使网络对输入模式响应的正确率不断提高，因而具有很好的非线性映射能力［15］。本文根据输入、输出样本的结构，设定神经网络的输入层和输出层的神经元个数分别为2 个和1 个。隐含层神经元个数参考经验公式(2)取为6 个。

其中，m 为输出层神经元个数，n 为输入层神经元个数，a 为［1，10］之间的常数。

1.3 智能控制力的确定

用训练好的BP 神经网络代替LQR 主动控制算法，根据结构实时的响应值可直接映射出所需的最优控制力的数值。

2 深水自升式海洋平台模型设计

按照结构模型试验的相似原理［16］，为了保证试验测试结果与平台原型响应的相似性，需要按照几何相似与动力相似进行设计，然而在模型设计过程中，要同时完全保证模型与原型的几何相似和动力相似是十分困难的。现有研究成果表明，振动控制系统的控制效果与结构振动的频响特性直接相关，因此，在综合考虑模型实际响应的效果以及本试验主要是以验证控制系统的有效性为实验目标后，在模型设计中主要满足几何相似和平台结构的振动频率尽量一致的相似准则。模型的缩尺比取为1∶40。实际设计模型与平台原型相关参数如表1 所示，平台模型的实物照片如图1 所示，浪向如图2 所示。

表1 实际模型与平台原型相关参数Tab. 1 Parameters of the real platform and the model

图1 平台试验模型Fig. 1 Experiment model of platform

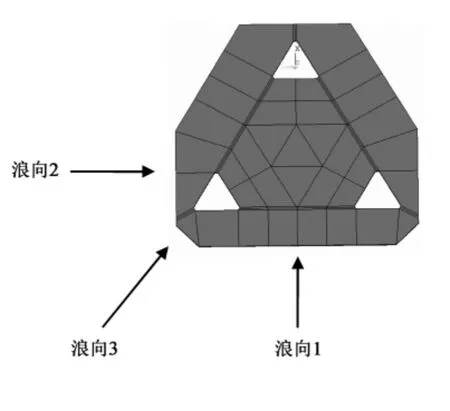
图2 浪向1、2、3Fig. 2 Wave directions 1，2，3

3 试验方案设计

3.1 试验工况设计

根据墨西哥湾实际海况以及水池试验条件，为了研究智能控制系统对不同工况的控制效果，分别选择3个规则波以及5 个不规则波工况进行水池试验，具体试验工况详见表2。其中，有义波高8 m、峰值周期10 s的真实海况理论上对应的试验值为0.2 m、1.58 s。

表2 试验工况Tab. 2 Experimental cases

3.2 测点布置设计

由于平台上部结构较平台下部结构的结构动力响应大，因此在如图3 所示的位置设置了4 个测点。测点4 安装的测量装置是六自由度非接触式运动测量系统，用于测量结构x、y 两个方向的位移;测点1、2、3 每处安装2 个加速度传感器，分别用于测量x 和y 方向的加速度响应。测量系统的示意如图4 所示。

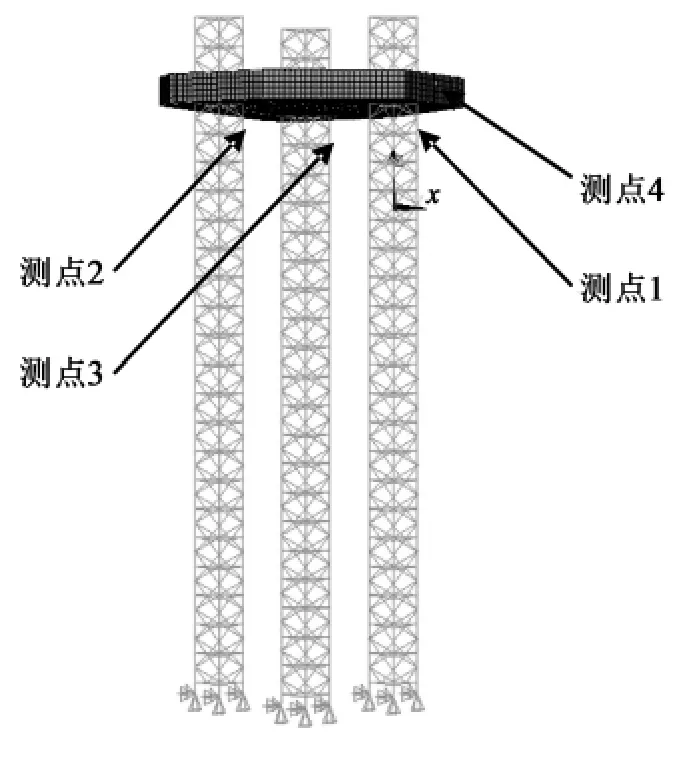
图3 测点布置位置Fig. 3 Measuring point position

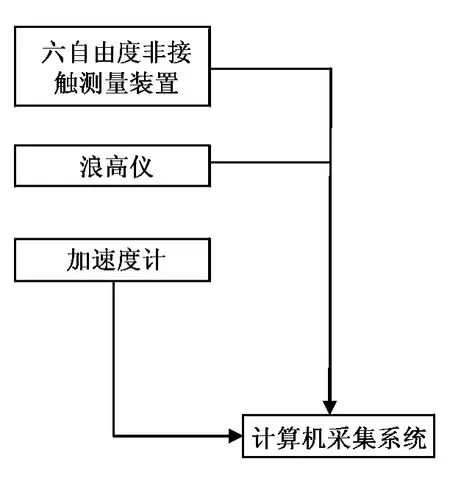
图4 测量系统Fig. 4 The measuring system

4 智能控制系统设计

4.1 磁流变阻尼器参数及安装位置

文中采用剪切阀式磁流变阻尼器作为智能控制器，其结构示意如图5 所示。

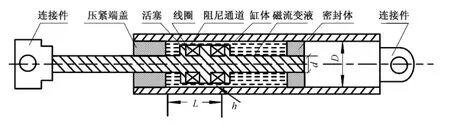
图5 磁流变阻尼器结构Fig. 5 MRFD structure figure

剪切阀式磁流变阻尼器阻尼力计算公式如式(3)所示:

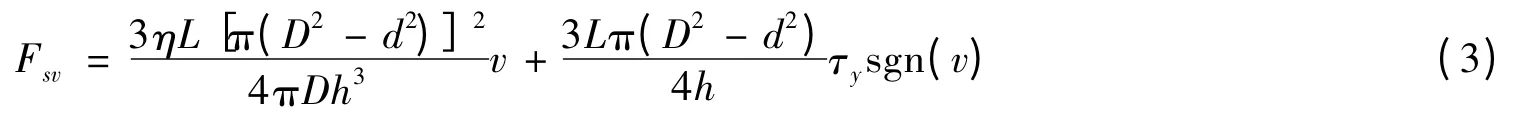
式中:η 为阻尼液的表观黏度;L 为导磁区长度;h 为阻尼通道高度;D 为缸体内径;d 为活塞直径;v 为活塞与缸体间的相对速度;τy为阻尼液的剪切屈服强度;sgn 为符号函数。

文中所选用磁流变阻尼器的具体性能参数如表3 所示，阻尼器的安装位置如图6 所示。

图6 阻尼器安装位置Fig. 6 Position of damper

表3 磁流变阻尼器基本参数Tab. 3 Parameter of MRFD

4.2 智能控制的具体流程

基于BP 神经网络的磁流变阻尼智能控制系统的控制流程如图7 所示。

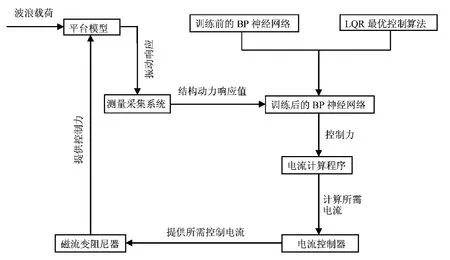
图7 智能控制系统控制流程Fig. 7 Structure of intelligent control system

5 实验结果及分析

本试验在适航性水池实验室完成。水池的主尺度为:长69 m、宽46 m、水深4 m。水池相邻的两边布置了三维摇板式造波机，造波机的造波能力为:规则波最大波高可达0.5 m，周期0.5 ～5 s;不规则波有义波高0.5 m，最大波高可达1.0 m;波向角0° ～180°。

为了验证控制系统的有效性，试验中分别测量了安装控制系统前后平台模型的动力响应，如图8 所示。限于篇幅，仅给出测点1 处的加速度响应以及测点4 处的位移和速度响应数据，如表4 所示。

图8 不规则波试验Fig. 8 Irregular experiment

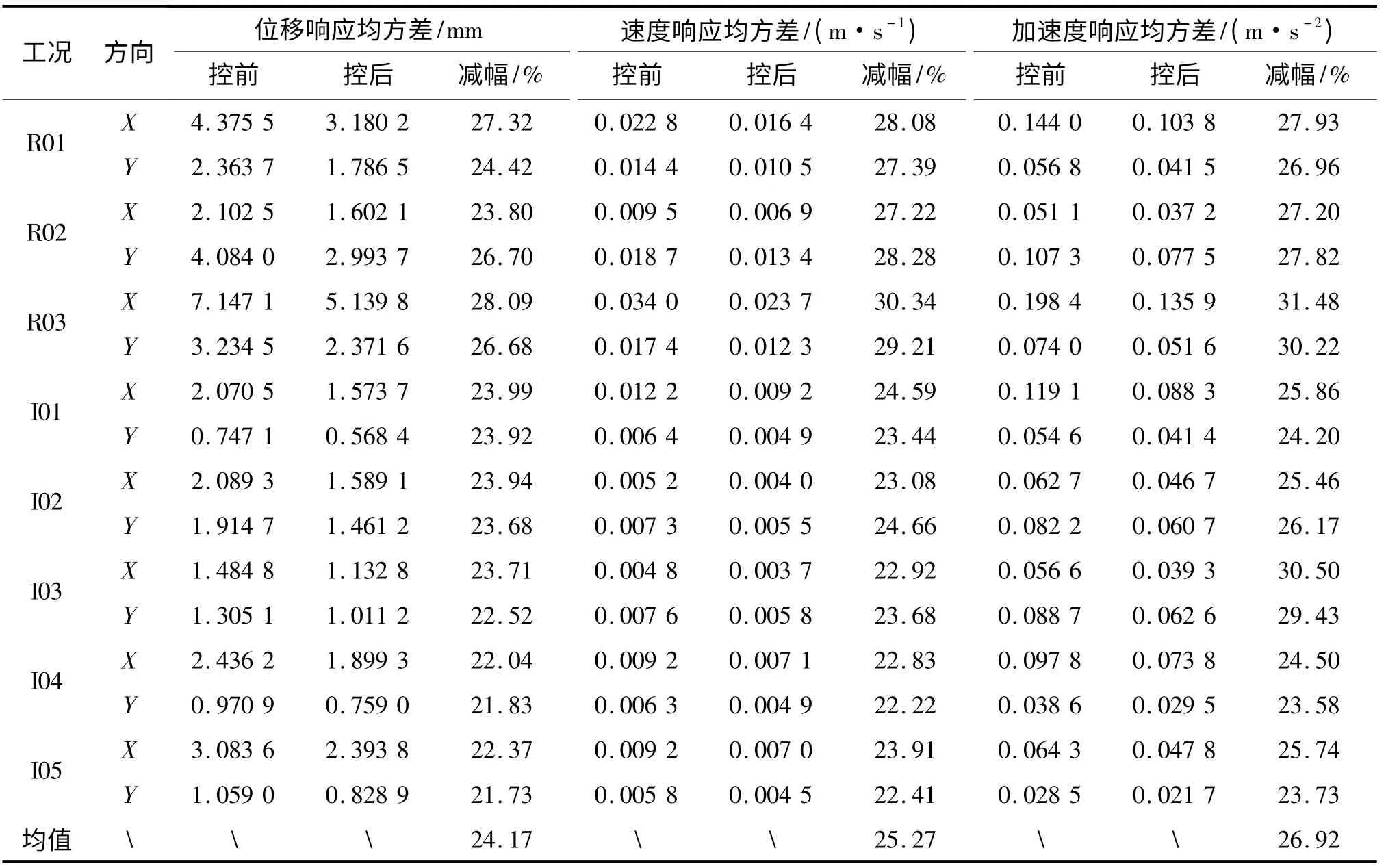
表4 振动响应减振效果Tab. 4 Vibration response control effect

图9 至图11 给出了I01 工况下控制前后测点4 处的位移、速度响应和测点1 处的加速度响应时程。

试验结果表明:基于BP 神经网络的磁流变阻尼智能控制系统能够对在波浪载荷作用下的平台试验模型的振动响应进行有效的控制，减振效果明显。其中，各种工况下位移的平均减振幅度达到24.17%，速度的平均减振幅度达到25.27%，加速度的平均减振幅度达到26.92%，这说明本控制系统对加速度响应的控制效果最好。

对比不同工况下的减振幅度发现:波高越大、周期越小，即波浪载荷越大、结构动力响应越剧烈时，本文所设计控制系统的减振效果越好。这与阻尼器的出力特点有关，因为阻尼器对剧烈的响应比较敏感，故结构响应大时阻尼器对结构动力响应的阻碍程度更大。

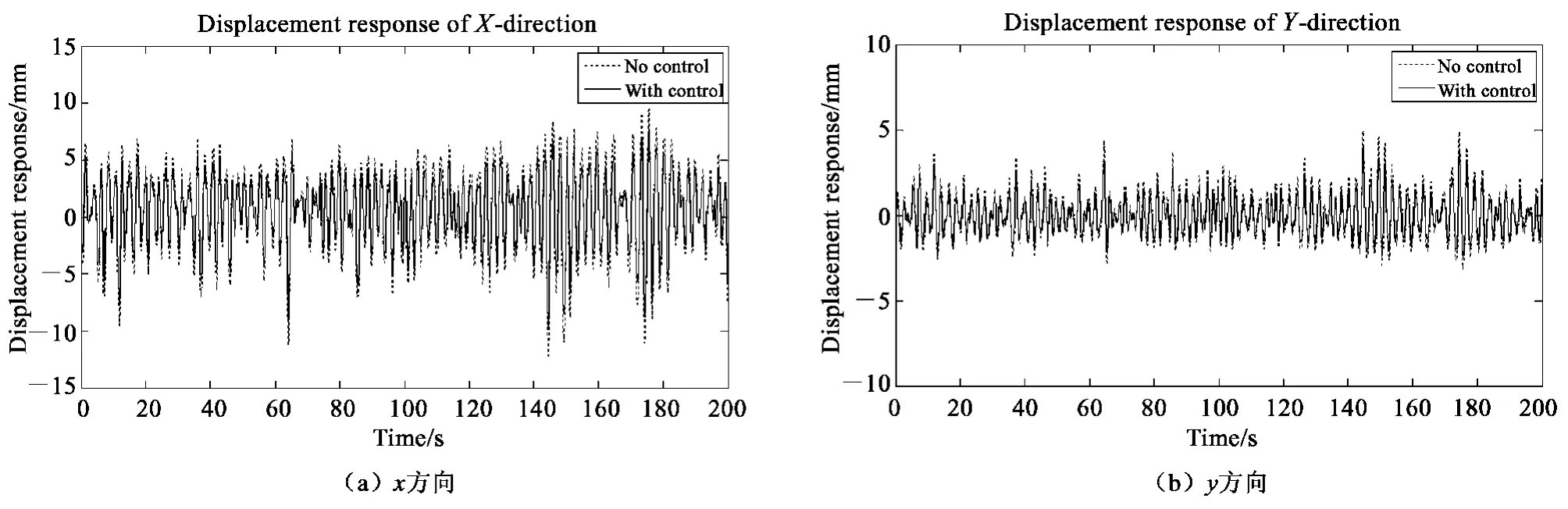
图9 位移减振效果Fig. 9 Displacement control effect

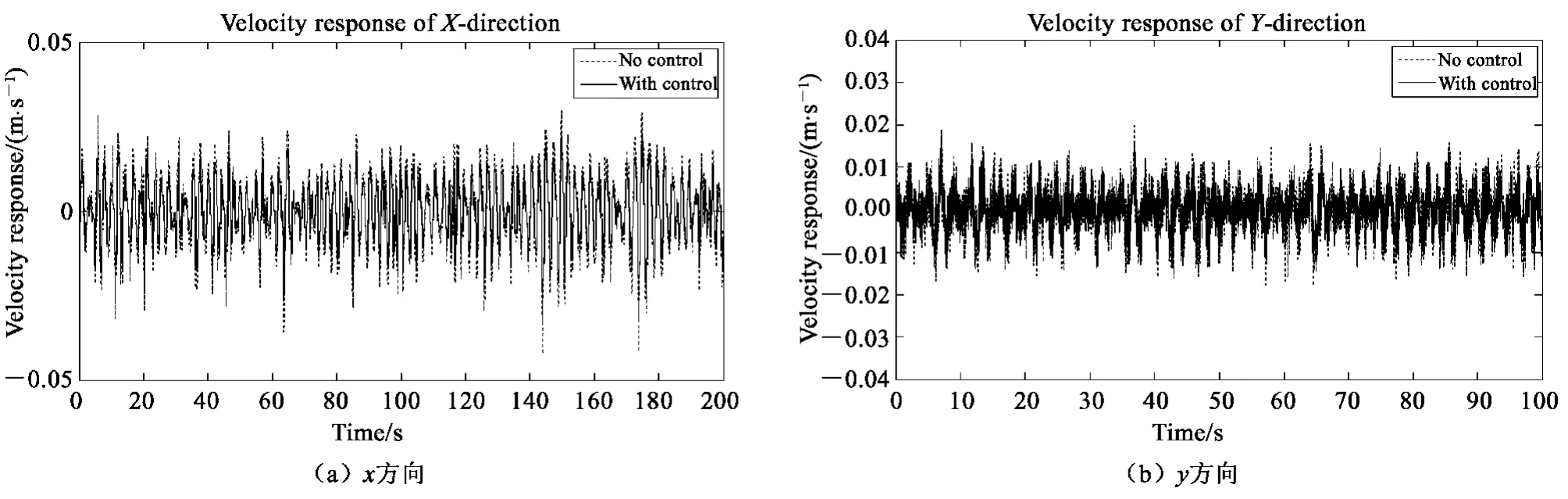
图10 速度减振效果Fig. 10 Velocity control effect

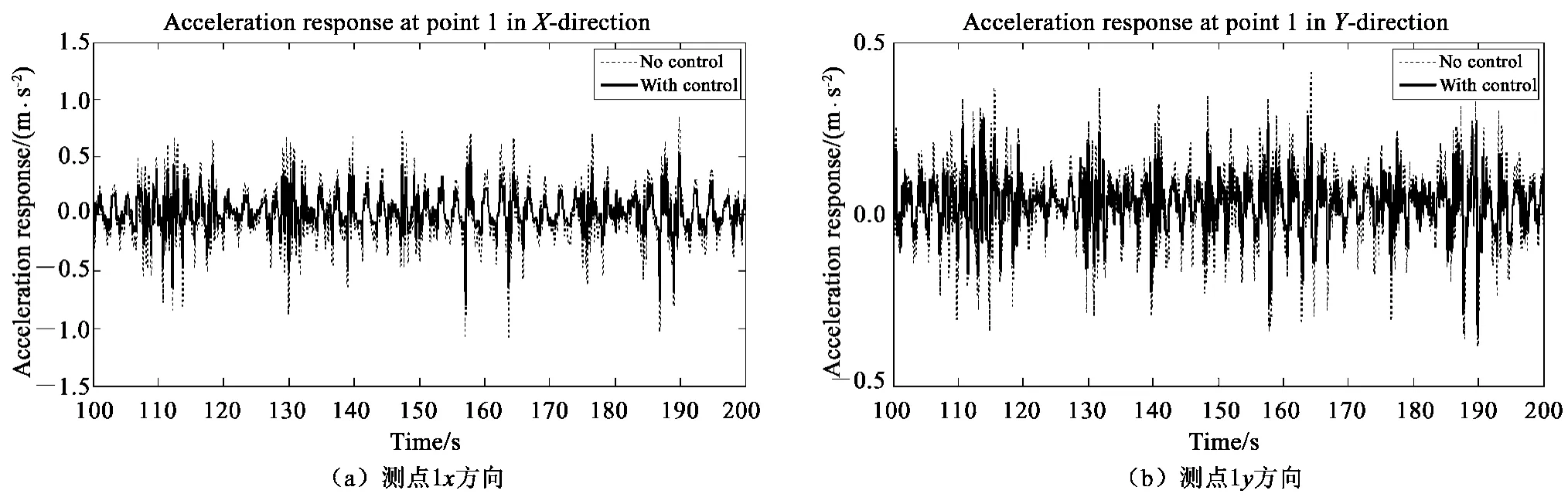
图11 加速度减振效果(时域)Fig. 11 Acceleration control effect (Time domain)

对比不同浪向下结构的减振幅度发现:结构沿波浪方向的动力响应减振效果更好。这主要是因为沿波浪方向的结构动力响应是因为波浪对结构的作用力而产生的，而垂直于波浪方向的结构动力响应是由结构沿浪向方向响应的排挤作用以及波浪因为结构的存在而发生的变形所引起的，在理想情况下不会存在垂直于波浪传播方向的结构响应，试验所设计的控制系统是根据理想情况设计的，故沿波浪传播方向的结构振动响应的控制效果较好。

同时试验结果还表明结构在规则波作用下的减振幅度略大于结构在不规则波作用下的减振幅度。

为了研究结构各个方向的频率特性，对测点1、2、3 测得的加速度信号进行了频域分析，限于篇幅，此处只给出R01 和I01 工况下控制前后测点1 处加速度响应的频域结果，如图12 至图13 所示。

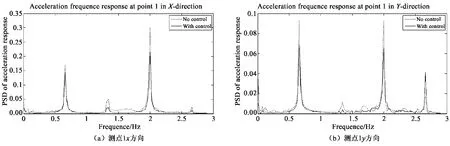
图12 工况R01 下加速度减振效果(频域)Fig. 12 Acceleration control effect under case R01 (Frequency domain)

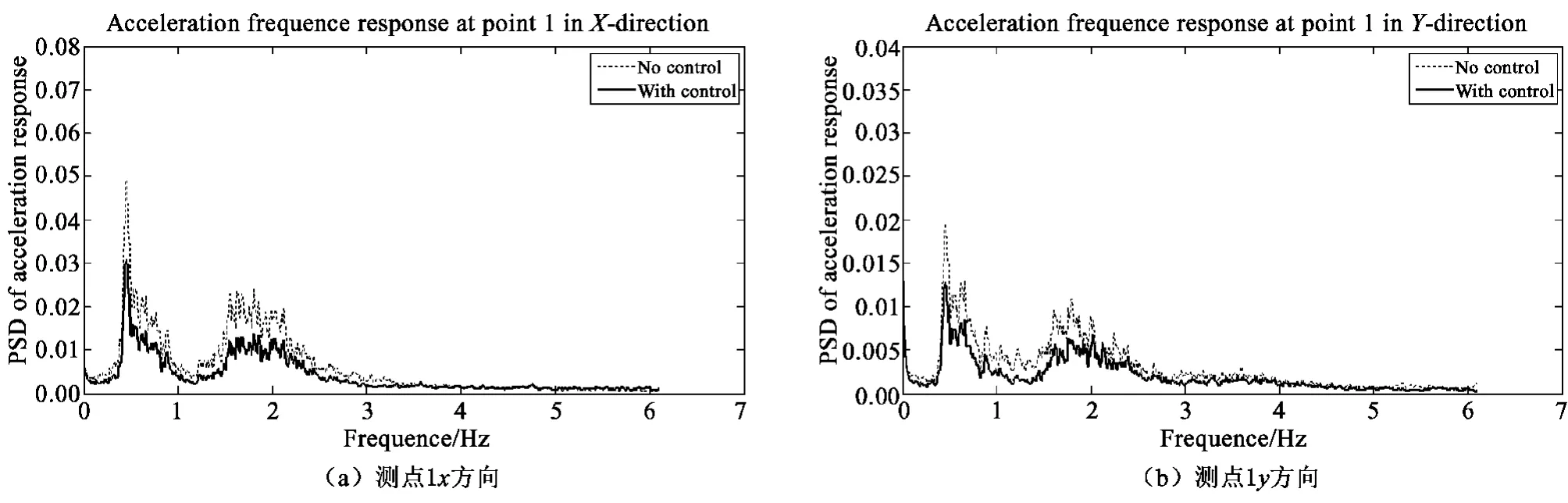
图13 工况I01 下加速度减振效果(频域)Fig. 13 Acceleration control effect under case I01(Frequency domain)

上述加速度响应的频域分析结果表明:

1)对于规则波，由于频率成分简单，因此频域响应的各个峰值明显。以工况R01 为例，在x 方向，结构振动主要集中在0.66 Hz 和1.98 Hz 这两个频率，其中，第一个频率为波浪的频率，第二个频率为结构的一阶固有频率，试验结果与实际情况较吻合。在y 方向，由于振动是由x 方向的振动引起，故频响的总体趋势一致，但是在2.7 Hz 左右出现了一个小的峰值，且在安装阻尼器后此峰值有所增大。经分析，该现象的原因可能是:此峰值反应的是阻尼器与结构连接装置的局部振动，安装阻尼器之后使得这一振动变得更为剧烈，因此反应为在该峰值处的加强。对比控制前后的频域响应可以发现，本文所设计的振动控制系统对结构的频域响应控制效果明显，且在峰值频率处的控制幅度最大。

2)对于不规则波，由于频率成分复杂，频响的频域分布较宽，频响峰值并不像规则波那样集中与突出，但结构频域响应的总体趋势仍然明显。以工况I01 为例，在x 方向，结构的响应仍然集中在波浪频率(0.4 Hz)和结构一阶固有频率(1.98 Hz)，与规则波频响分析结果一致，在y 方向亦如此。在不规则波浪作用下，本文所设计的振动控制系统对频响的各个频率成分均起到振动控制的作用，尤其是对于峰值频率处的振动控制幅度最大。

6 结 语

本文针对自升式海洋平台，给出了智能控制系统、海洋平台模型以及水池模型试验的设计方法，通过模型试验的方式研究了基于BP 神经网络的智能控制系统对波浪载荷作用下深水自升式海洋平台振动响应的控制效果。试验结果表明:

1)基于BP 神经网络的磁流变阻尼智能控制系统能够很好地控制波浪载荷作用下深水自升式平台的结构动力响应，减振幅度比较可观，位移、速度、加速度的减振幅度均能达到20%以上，其中，对加速度的减振效果最好;

2)本控制系统对不同工况下平台结构动力响应的控制效果较稳定，具有好的鲁棒性能，但是相对于不规则波而言，结构在规则波作用下时控制系统的减振效果较好，且控制系统对沿浪向方向的振动响应控制效果较好，对结构较剧烈的响应比较敏感;

3)不同于被动控制系统，本控制系统不仅有效抑制了结构基频处的动力响应，而且对各个频率处的动力响应均可起到振动控制的作用，尤其是对波频响应亦表现出了较好的减振效果，控制性能优秀。

［1］罗宏志，蒙占彬.国内深水自升式钻井平台发展概况［J］.中国海洋平台，2010，25(4):4-7.

［2］汪张棠，赵建亭.我国自升式钻井平台的发展与前景［J］.中国海洋平台，2008，23(4):8-13.

［3］M J Cassidy，R Eatock Taylor，G T Houlsby.Analysis of jack-up units using a constrained New-wave methodology［J］.Applied Ocean Research，2001，23:221-234.

［4］何晓宇，李宏男.波浪载荷作用下导管架海洋平台利用TLCD 的振动控制［J］.振动工程学报，2008，21(1):71-78.

［5］赵 东，马汝建，王威强，等.ETMD 减振系统及其在海洋平台振动控制中的应用［J］.西安石油大学学报:自然科学版，2006，21(2):57-61.

［6］张海廷，马汝建，赵 东.海洋平台减振装置设计及振动控制仿真研究［J］.船海工程，2010，39(5):226-229.

［7］DENG Z C，ZHANG D G.Experimental research on the vibration reduction and impact resistance performances of offshore structure based on magnetorheological damper［C］∥Proc.of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering.2008.

［8］欧进萍，王 刚，田石柱.海洋平台结构振动的AMD 主动控制试验研究［J］.高技术通讯，2002，12(10):85-90.

［9］杨 飏，欧进萍.导管架式海洋平台结构磁流变阻尼隔震的振动台试验［J］.地震工程与工程振动，2005，25(4):141-148.

［10］张纪刚，吴 斌，欧进萍.海洋平台冰振控制试验研究［J］.东南大学学报:自然科学版，2005，35(z1):31-34.

［11］嵇春艳，万乐坤，尹 群.海洋平台磁流变阻尼器控制技术研究［J］.海洋工程，2009，26(3):27-32.

［12］霍发力，嵇春艳，李珊珊，等.基于模糊理论海洋平台的MRFD 半主动控制理论研究［J］.中国海洋平台，2009，24(1):31-35.

［13］嵇春艳，陈明璐，霍发力，等.波浪荷载作用下海洋平台半主动控制试验研究［J］.江苏科技大学学报:自然科学版，2010，24(4):315-318.

［14］欧进萍.结构振动控制——主动、半主动和智能控制［M］.北京:科学出版社，2003.

［15］李宏男，李忠献，祁 皑，等.结构振动与控制［M］.北京:中国建筑工业出版社，2005.

［16］杨俊杰.相似理论与结构模型试验［M］.武汉:武汉理工大学出版社，2005.