沉入式大圆筒码头稳定性有限元强度折减法分析

王元战，蔡雅慧，王禹迟

(天津大学 建筑工程学院，天津市港口与海岸工程重点实验室，天津 300072)

大直径薄壁圆筒(简称大圆筒)结构是一种新型港口水工建筑物结构，具有造价低、工期短，适用于软土地基和恶劣海况等复杂条件的优势，拥有广阔的应用前景。然而，沉入式大圆筒结构受力条件及其作用机理复杂，目前尚缺乏广泛认可的理论体系与计算方法，稳定性分析方法无规范或标准可循。随着有限元技术的发展，利用有限元数值模型分析新型结构力学特性成为一种有效的途径。

对于沉入式大圆筒等新型防波堤结构，由于承受的外载荷主要是波浪力，针对这一特点，近年来提出了新型防波堤结构稳定性分析的有限元加载系数法。其基本思想是，在有限元模型计算过程中，逐步增加波浪力，直至结构发生稳定性破坏，此时的波浪力即为结构的极限承载力。为表述清楚，定义一个表征荷载加载程度的加载系数:

α = P/PD

式中:P 为加载波浪力，PD为设计波浪力。

当加载到结构极限承载力Pu 时，加载系数即定义为结构稳定性安全系数K。

文献［1-4］利用加载系数法计算分析了沉入式大圆筒防波堤、箱筒型基础防波堤、半圆型防波堤、倒T型导管墙桩基防波堤等新型防波堤结构的稳定性，并在此基础上进一步分析土与结构相互作用关系，建立更为合理有效的简化计算方法等。

然而，对于沉入式大圆筒等新型码头结构，其承受的外部荷载复杂，除了波浪力作用，还有墙后填料产生的土压力，筒前低水位和筒后地下水位差引起的剩余水压力，船舶荷载，堆货荷载、流动机械荷载等各种地面使用荷载以及码头面可变荷载作用产生的土压力［5］等。此外，对码头结构进行稳定性分析时，必须考虑各种不利情况下的荷载组合，显然，利用加载系数法进行码头结构的稳定性分析变得十分困难。

强度折减法是通过土体强度参数的降低来实现对失稳情况的模拟，近年来被广泛应用于边坡稳定性分析中。文献［6-7］采用强度折减法进行边坡稳定性分析，以非线性有限元静力计算不收敛时的折减系数作为边坡稳定性安全系数，并得到边坡破坏时的滑动面。算例表明采用摩尔—库仑等面积圆屈服准则时，强度折减法求得的稳定安全系数与传统计算方法非常接近，证实了该方法的实际可行性。文献［8］针对某一典型边坡算例，分别依据计算的收敛性、特征部位位移的突变性和塑性区的贯通性等3 个失稳判据，采用强度折减法进行边坡稳定性分析。通过对比Spencer 极限平衡法的计算结果，建议联合采用特征部位位移的突变性和塑性区的贯通性作为边坡的失稳判据。文献［9］将强度折减法应用于边坡稳定性的三维分析，通过对比传统极限平衡法和二维分析的结果，验证了三维分析的可行性，认为采用有限元法对边坡稳定性进行分析时，二维分析难以较好地模拟边坡复杂的地质、地形、地势等实际条件，因此，在有条件的情况下，尤其是对大型边坡和重要工程，宜补充进行三维分析。文献［10］认为土体强度参数c、φ 在边坡失稳破坏时的发挥程度、发挥秩序以及衰减速度、衰减程度并非完全相等，提出了双系数折减法，即在强度折减过程中对c、φ 采用不同的折减系数，而不同的折减方法将对应不同的安全系数和滑动带，使边坡的可能滑动位置变成一个可能滑动区域。

沉入式大圆筒结构的抗滑、抗倾稳定性靠地基土的嵌固作用来维持，在极限状况下，认为外载荷所产生的土体实际剪应力与土体抵御外载荷所能发挥的最低抗剪强度相等［11］，即，当不断折减土体的实际强度指标直至达到极限破坏状态时，外载荷所产生的剪应力与强度折减后所确定的土体抗剪强度相等，可通过弱化土体强度来实现对结构极限破坏状态的模拟。基于上述假设，并在沉入式大圆筒防波堤结构工程算例验证的基础上，建立了沉入式大圆筒码头结构稳定性分析的有限元强度折减法。结合工程实例，利用有限元软件ABAQUS，采用有限元强度折减法计算沉入式大圆筒码头结构的稳定性安全系数。

1 有限元强度折减法

有限元强度折减法是强度折减技术与弹塑性有限元方法的结合，其基本原理是:在有限元计算中，逐步折减土体的抗剪强度参数——粘聚力C 和内摩擦角的正切值tanφ，直至土体达到极限破坏状态，定义强度折减法的安全系数Fv为:

Fv= τ/τ'

式中:τ 为土体的初始抗剪强度，τ'为强度折减后极限状态下的土体抗剪强度［12］。

不同的屈服准则下，土体抗剪强度的表达式不同，以摩尔—库伦准则为例:τ =c +σtanφ。因此，强度折减过程可表示为:

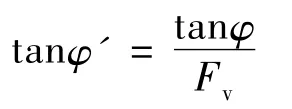
可见，强度折减法对于安全系数的定义与传统极限平衡法一致，亦是一种强度储备安全系数。在传统极限平衡法下，当土体达到极限状态(即安全系数为1)时，破坏面上的土体抗剪强度参数C 和tanφ 值降为c'和tanφ'。因此，强度折减法中的土体折减系数即为安全系数Fv。

综上，采用有限元强度折减法进行稳定性分析，就是在有限元计算过程中，将土体的强度参数——粘聚力C 和内摩擦角的正切值tanφ 折减一个系数，生成一组新的土体参数，再代入有限元计算模型进行试算，以位移、广义剪应变等描述变形程度的某种物理量作为评判指标［13］，判断土体是否达到极限破坏状态。反复进行上述步骤，当土体达到极限平衡时，其强度参数的折减系数，就是稳定性安全系数值［14］。

2 工程概况

2.1 沉入式大圆筒码头结构方案

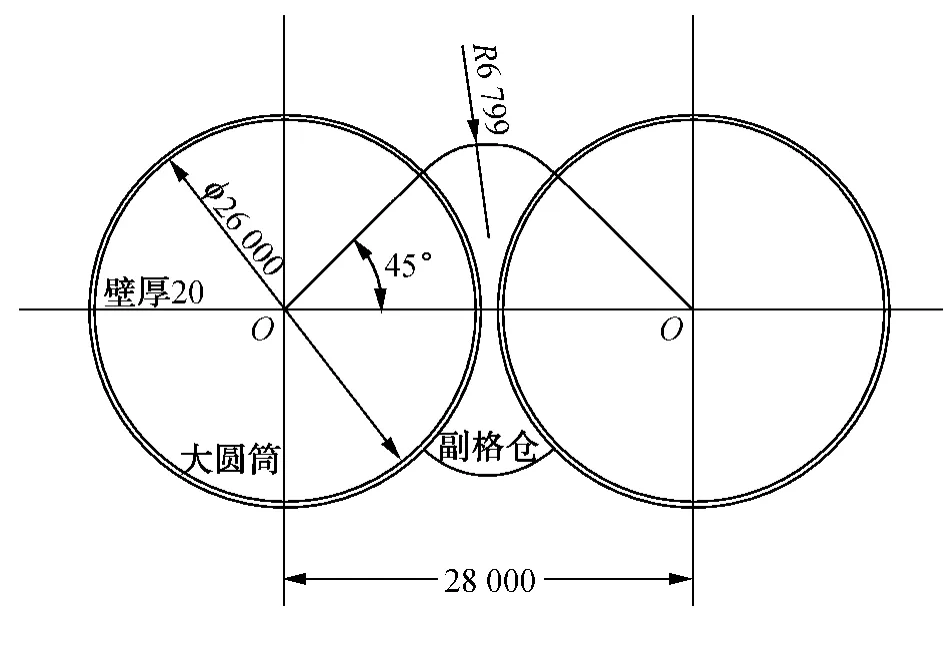
图1 沉入式大圆筒结构平面示意(单位:mm)Fig.1 Plane of the embedded large cylinder structure(unit:mm)

某港码头结构方案之一是沉入式大圆筒结构。码头顶高程为9.50 m，考虑构建5 m 高的胸墙，圆筒结构顶高程设为4.50 m，筒底入土至－50.00 m。采用钢质圆筒，直径26 m，壁厚20 mm，结构平面如图1 所示。

港区原泥面高程为－10.00 m，码头前沿开挖至－19.50 m。大圆筒筒内及筒后回填中粗砂，码头后方采用吹填砂。考虑到建筑物上部结构自重较大，门机等荷载也较大，该方案在码头前方胸墙及轨道梁下加设了部分长桩，将上部荷载直接传入下层地基，以减小结构变形。长桩底端入土至－60.00 m，码头结构断面如图2 所示。

在结构稳定性分析中，由于基桩的存在有利于沉入式圆筒码头结构的稳定，为使计算偏于安全，计算中暂不考虑基桩的作用。简化后的大圆筒结构计算断面如图3 所示。

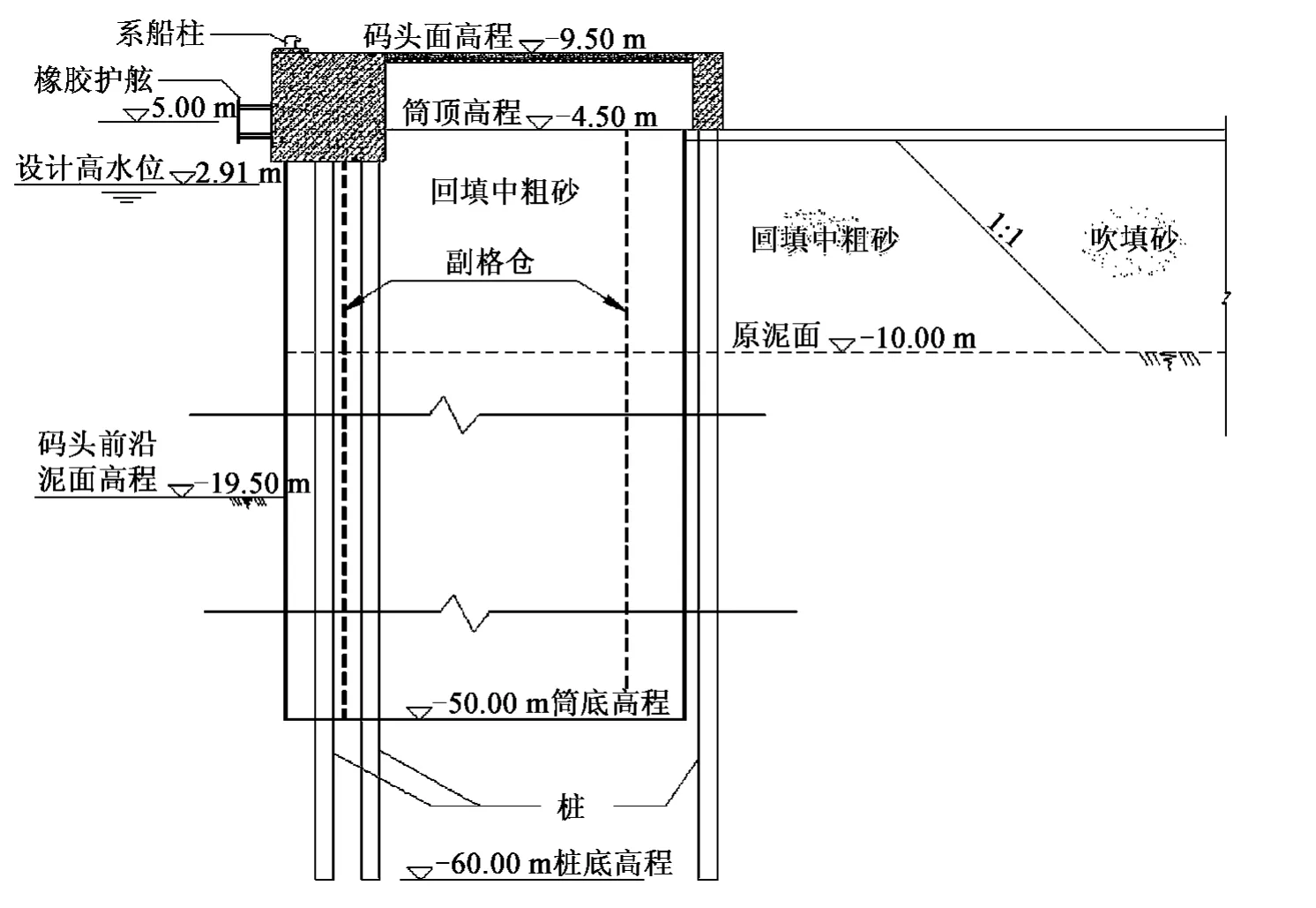
图2 沉入式大圆筒码头结构断面示意Fig.2 Section view of the embedded large cylinder quay

计算工况采用设计高水位+50年一遇波浪作用，设计波浪按S 方向考虑;剩余水头采用1/3 平均潮差;堆货荷载取用20 kPa;筒顶承受胸墙等码头上部结构的自重作用。

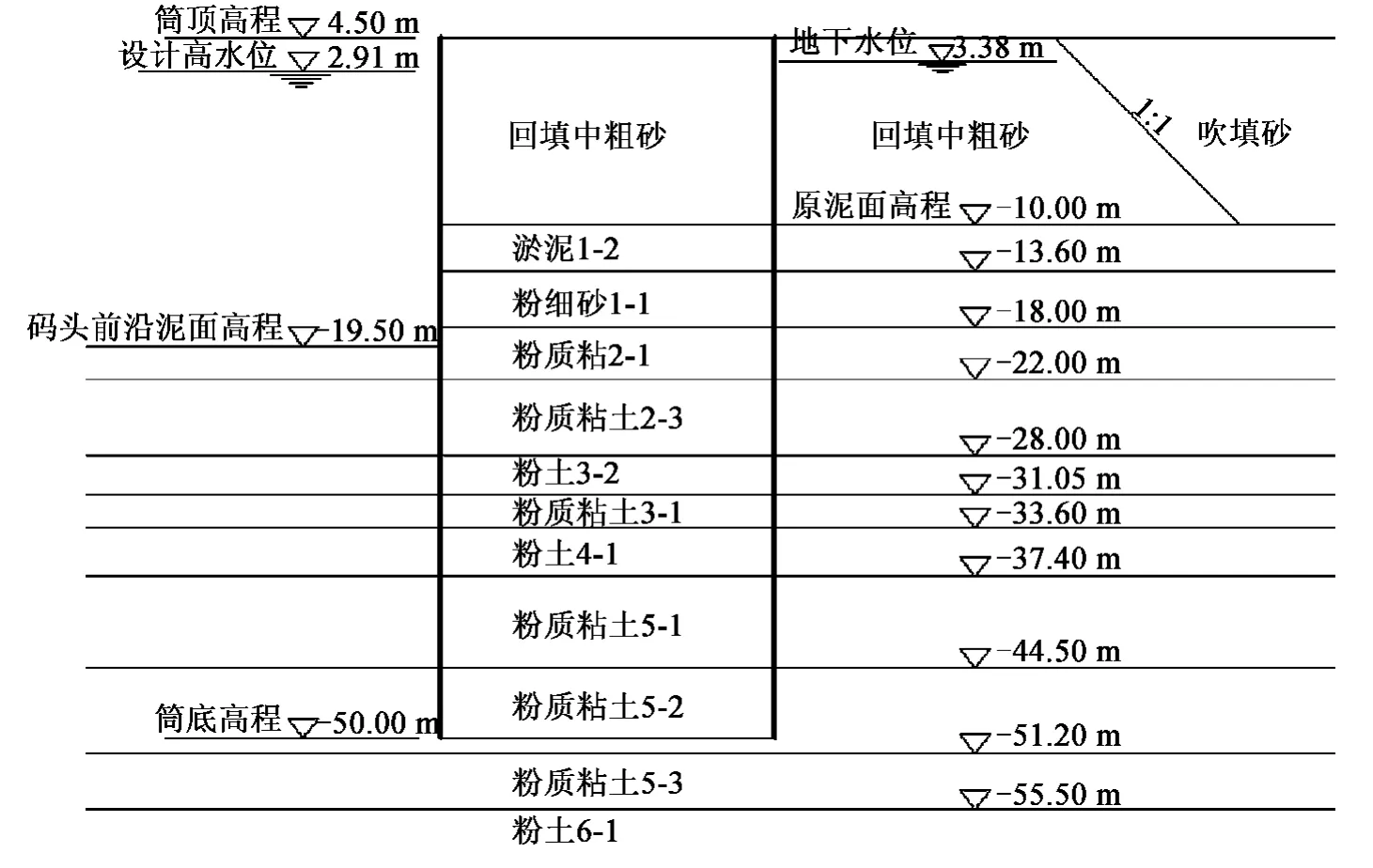
图3 简化后的沉入式大圆筒码头结构计算断面Fig.3 The simplified calculation section view of the embedded large cylinder quay

2.2 土性指标

各层土性指标见表1。

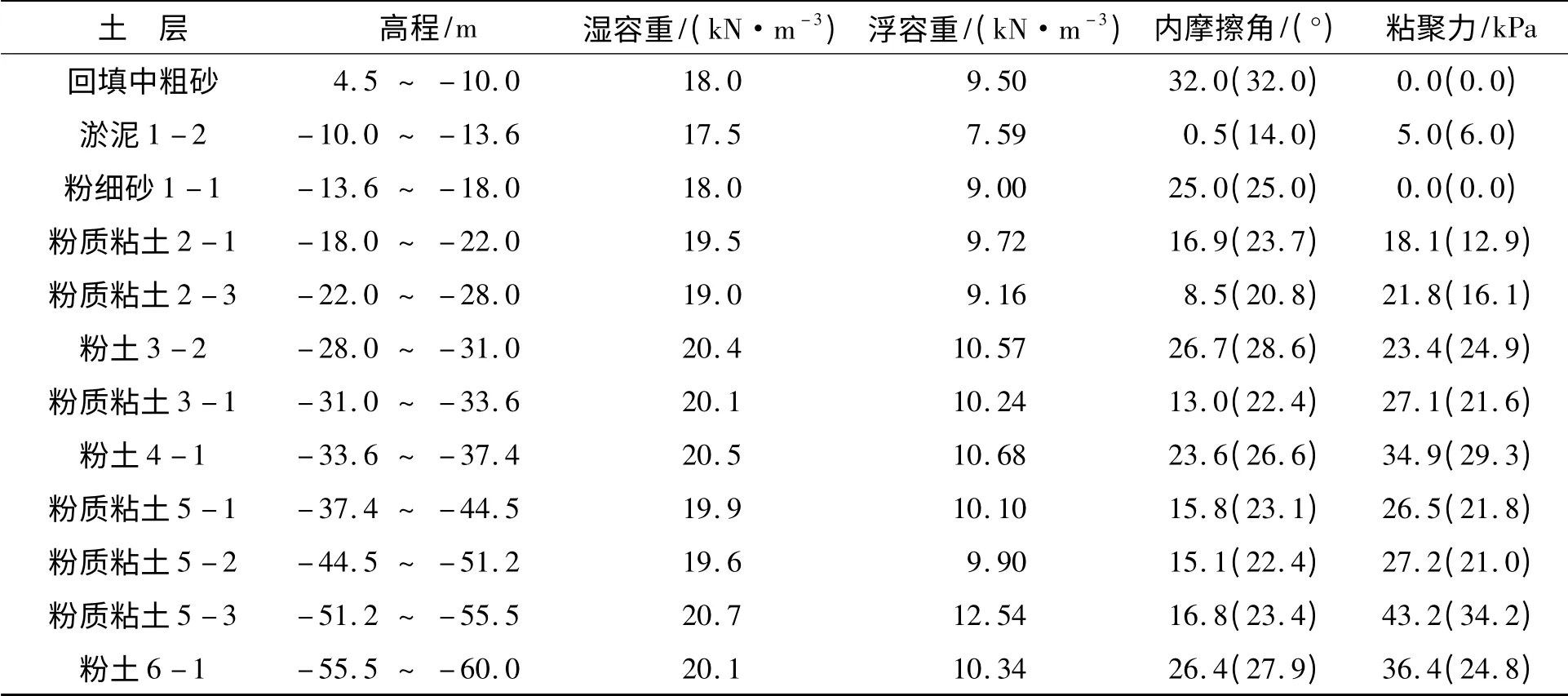
表1 不同土层土体参数Tab. 1 Different soil parameters

2.3 设计水位及波浪条件

设计水位和波浪条件如表2 和表3 所示。

表2 工程设计水位Tab. 2 Engineering design level

表3 工程波浪条件Tab.3 Engineering wave conditions

连续圆筒结构上的波浪力，按平面直墙波浪力计算方法确定，波峰作用时考虑0.9 左右的折减系数，波谷作用时考虑0.95 左右的折减系数。计算中为保守考虑取折减系数为1，且考虑最不利荷载——波吸力的作用。

码头前沿泥面标高为－19.50 m，根据波浪条件，码头前沿水深且d ＞H，故墙前产生立波。根据文献［15］相应的计算公式，得静水面处波浪压强p0=0 kPa，静水面以下深度H－hs处波浪压强ps=41.62 kPa(hs为波浪超高)，水底处波浪压强pd=18.90 kPa，墙面波浪压强分布如图4所示，单位长度墙面上总波浪力P=639.68 kN/m。

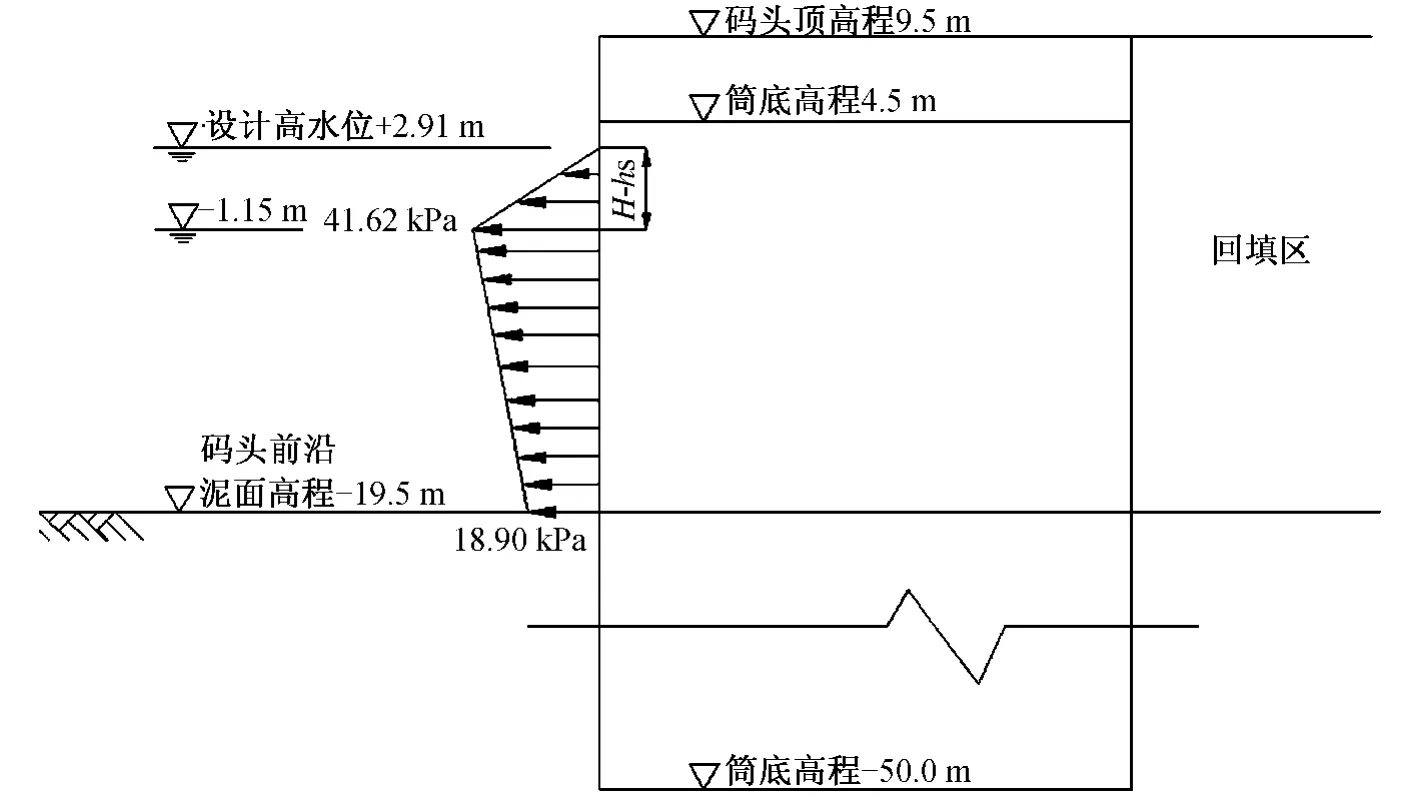
图4 码头墙面波浪压强分布Fig.4 Distribution of the wave pressure on the surface of the quay

3 有限元分析模型

3.1 整体模型及边界条件

大圆筒码头结构由一系列圆筒薄壳连续排列构成，具有连拱形墙面，空间承载特性明显。采用有限元方法，利用有限元分析软件ABAQUS，建立大圆筒码头结构与土相互作用的三维弹塑性整体分析模型。为便于分析，假设波浪荷载的作用方向垂直于墙轴线，根据荷载及结构的空间对称性，在垂直于墙轴线方向取一个圆筒的一半和前后一定范围的土体作为建立有限元模型的区域，在边界上施加对称边界条件。其中，土体的计算域为:在垂直防波堤轴线方向，向两侧各取大圆筒直径尺寸的5 倍;在深度方向，筒体以下取3 倍的圆筒入土深度。整体计算域平面示意和立面示意分别如图5 和图6 所示。计算域边界条件为:地基表面为自由边界，底面为固定边界，前侧面和后侧面为侧限边界，左侧面和右侧面为对称边界。

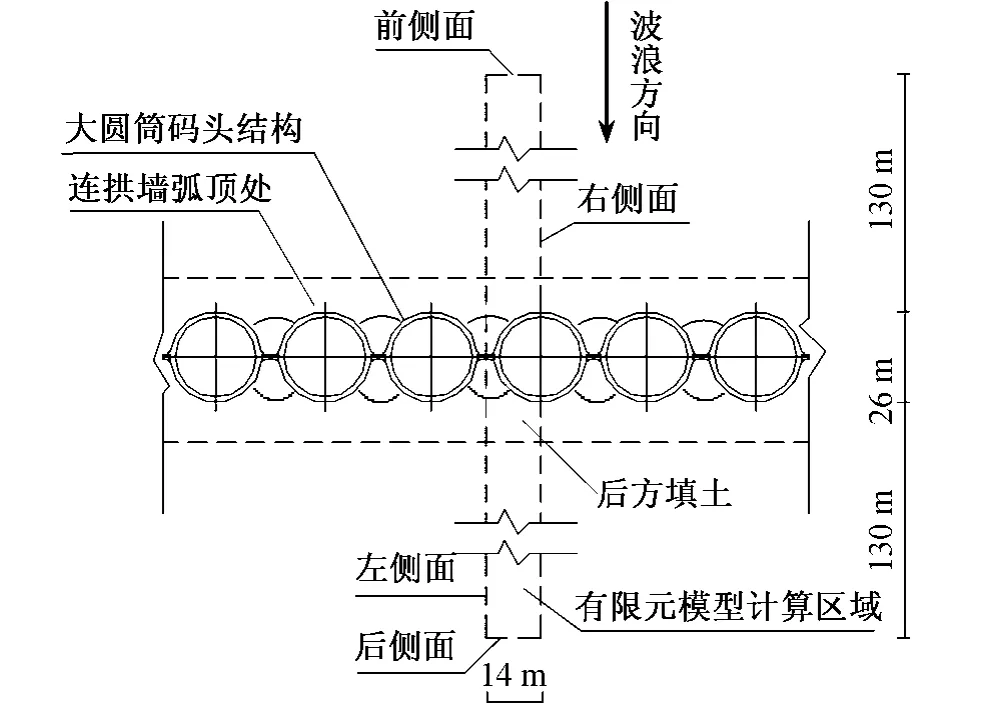
图5 有限元计算域平面示意Fig.5 Plane of finite element calculation domain

图6 有限元计算域立面示意Fig.6 Elevation of finite element calculation domain

3.2 结构及土体模拟

由于大圆筒结构由钢材制成，结构强度和刚度远远大于土体强度和刚度，结构系统的位移和失稳破坏主要决定于地基土的变形和承载能力，故在有限元分析中大圆筒结构采用弹性模型，计算中大圆筒结构参数取用弹性模量E=210 GPa，泊松比μ=0.3。土体本构模型采用C-M 模型。在建立的三维有限元模型中，土体和结构均采用八节点三维减缩积分实体单元。

3.3 土体与结构接触面模拟

在结构物与地基相互作用问题中，由于和土体材料相比，结构材料具有很高的强度和刚性。因此，在应力作用下，接触面上土体和结构难以协调变形，容易产生接触面的分离和相对错动，需要在结构与土体接触的区域(包括大圆筒的内外壁及底部与土体接触的区域)引入接触面单元，建立主从接触面，以模拟在波浪力、剩余水压力、堆货荷载等外载荷作用下结构与周围土体的粘结、滑移和脱离现象。考虑到结构的弹性模量远大于土体的弹性模量，指定结构上的接触面为主接触面，土体上的接触面为从接触面。

土体与结构的接触行为是一个高度非线性的问题，在接触面上需要确定不同时刻接触区域不同位置处的动接触状态以及接触行为的本构模型。在建立三维弹塑性耦合分析模型时，接触单元的本构模型切向采用库仑摩擦本构模型;法向采用硬接触方式，即假定相互作用的两个物体，相互挤压时不产生浸入变形，受法向拉力时在接触面上产生分离。

土与结构相接触区域的不同位置处的接触状态是随着时间不断发生变化的，分为三种接触状态，即分离状态、粘结接触状态及滑动接触状态。当处于分离状态时，接触力为零;当处于粘结接触状态时，主从接触面相互挤压，但无相对滑动，摩擦力处于静摩擦状态。

3.4 稳定性分析方法

3.4.1 稳定性分析步骤

基于强度折减法原理，采用有限元方法进行波浪力、剩余水压力、堆货荷载等外载荷作用下沉入式大圆筒码头结构稳定性分析的步骤如下:

1)建立有限元分析模型。

2)根据波浪力、剩余水压力、堆货荷载、上部结构自重等外载荷的分布，在结构上相应位置施加设计荷载，计算在设计荷载作用下土与结构体系的位移和应力。

3)逐级降低有限元分析模型中全部土体的强度参数(包括粘聚力C 和内摩擦角的正切值tanφ)，计算相应土体强度下土与结构体系的位移和应力，直至有限元计算不收敛。

4)绘制折减系数——结构位移关系曲线。

5)确定依据折减系数——结构位移关系曲线判别结构失稳的准则。

6)根据失稳判别准则，确定结构稳定性破坏对应的折减系数，将该系数定义为结构稳定性安全系数。

3.4.2 失稳判别准则

虽然强度折减法的基本原理简单，近年来也在边坡稳定性分析中得到了广泛的应用，但目前尚缺乏统一的失稳评判标准。同时，由于边坡失稳与结构失稳的模式不同，现有的强度折减法边坡失稳判据也不能完全适用于判别大圆筒码头结构的稳定性。

考虑到强度折减法的基本思想与传统的极限平衡法一致，均可称之为强度储备安全系数法，即主要考虑的是力和强度之间的关系问题。结合结构极限承载力判别标准，以折减系数——结构位移关系曲线(即FV-S曲线)斜率接近于零时对应的折减系数为结构的稳定性安全系数，此时即使增加微小的折减系数，结构也将发生非常大的变位，说明结构已经破坏。该判别准则精确、可靠，可避免由于其他原因造成有限元计算不收敛而导致的判别错误。

4 有限元计算结果分析

4.1 方法验证

为了验证本文所建立的结构稳定性分析有限元强度折减法的正确性，将其应用于某一沉入式大圆筒防波堤工程实例的稳定性分析，并将计算结果与防波堤稳定性分析的有限元加载系数法进行对比。

沉入式大圆筒防波堤采用钢质圆筒，直径22 m，壁厚16 mm，筒顶标高8.50 m，筒底入土至－49.00 m。港区原泥面高程为－19.00 m，筒内泥面以上回填块石。各层土性指标见表4。钢质圆筒材料参数取用弹性模量E=210 GPa，泊松比μ=0.3。

图7、图8 分别给出了所选沉入式大圆筒防波堤结构在计算工况1:极端高水位+50年一遇波浪作用，结构顶高程为8.50 m 和计算工况2:设计高水位+10年一遇波浪作用，结构顶高程为4.00 m 条件下，强度折减法计算所得折减系数——结构转角关系曲线和加载系数法计算所得波浪力加载系数——结构转角关系曲线。

表4 不同土层土体参数Tab.4 Different soil parameters

图7 工况1 和工况2 折减系数-结构转角关系曲线Fig.7 Curved line of reduction factor and structural rotation angle for calculated Case 1 and Case 2

图8 工况1 和工况2 加载系数－结构转角关系曲线Fig.8 Curved line of loading coefficient of structural rotation angle for calculated Case 1 and Case 2

根据所建立的结构稳定性分析强度折减法的失稳判别准则和有限元加载系数法常用的极限承载力判别标准，将强度折减法与加载系数法的结构稳定性分析计算结果列于表5。

表5 强度折减法与加载系数法计算结果的对比Tab.5 Comparison of the calculated results of strength reduction and loading coefficient method

由对比结果可以看出，有限元强度折减法与加载系数法对于大圆筒防波堤结构的稳定性分析结果一致性良好，两种方法计算得出的结构稳定性安全系数基本相同。说明有限元强度折减法适用于结构的稳定性分析，且具有较高的精度，验证了所建立的有限元分析方法的正确性。

4.3 特征点的选取

图9 特征点分布示意Fig.9 Distribution of the feature points

为便于分析，选取迎浪侧圆筒结构顶部端点及码头前沿泥面处筒体内壁上的结点作为分析特征点，如图9 中A 点、B 点所示。通过特征点的折减系数—位移关系曲线可以方便地得到结构变位并以此判断结构的稳定性。

由于结构整体刚度远大于地基刚度，可以看成刚体。定义A、B 两点间水平位移差与两点间距的比值的反正弦值为结构转角θ，即:

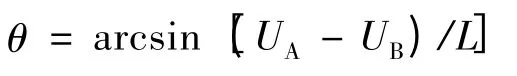
式中:UA、UB分别表示A 点、B 点的水平位移，L 表示A 点和B 点之间的距离。

4.3 结构稳定性安全系数

图10 和图11 分别给出了本文所建立的沉入式大圆筒码头结构有限元分析模型计算所得结构特征点折减系数—水平位移和折减系数—结构转角关系曲线。

从图中可以看出，当土体强度采用快剪指标时，曲线斜率在折减系数为1.80 时接近于0，此时即使增加微小的折减系数，结构也将产生非常大的位移/转角变位，说明结构已经失稳破坏，即达到极限破坏状态。因此，快剪指标强度下，大圆筒结构的稳定性安全系数为1.80，筒顶高程处的水平位移为4.31 m，筒体转角为0.073 rad。当土体强度采用固结快剪指标时，曲线斜率在折减系数为2.20 时接近于0，此时再增加微小的折减系数，结构将产生非常大的位移/转角变位，结构失稳破坏。因此，固结快剪指标强度下，大圆筒结构的稳定性安全系数为2.20，筒顶高程处的水平位移为4.26 m，筒体转角为0.073 rad。计算结果列于表6。

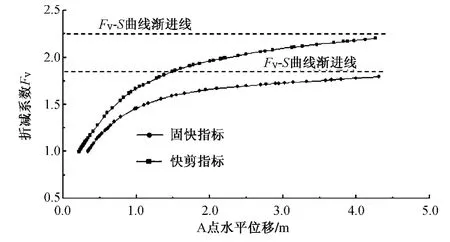
图10 折减系数－筒顶水平位移关系曲线Fig.10 Curved line of reduction factor and top end structural horizontal displacement

图11 折减系数－结构转角关系曲线Fig.11 Curved line of reduction factor and structural rotation angle

表6 有限元强度折减法计算结果Tab. 6 The calculated results of strength reduction FEM

4.4 结构应力及土体塑性变形

当结构达到极限破坏状态时，结构应力云图和土体塑性变形分别如图12 和图13 所示。

图12 极限破坏状态下结构应力云图Fig.12 The structural stress nephogram under ultimate failure state

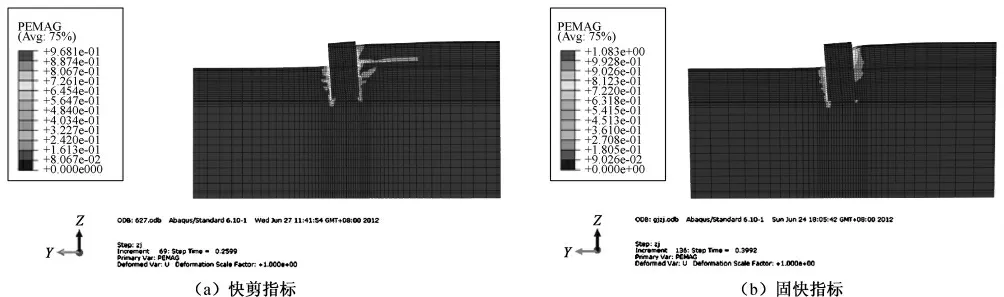
图13 极限破坏状态下土体塑性变形Fig.13 The soil plastic strain diagram under ultimate failure state

5 结 语

建立了沉入式大圆筒码头结构稳定性分析的有限元强度折减法。结合工程实例，分析了沉入式大圆筒码头结构的稳定性。通过沉入式大圆筒防波堤工程算例，证明了有限元强度折减法对结构的稳定性分析结果与有限元加载系数法较为一致，验证了该方法的可靠性。

有限元强度折减法原理简单，利用其进行结构稳定性分析时只需要对土体的强度参数进行弱化，操作简单，适用于码头结构等作用荷载复杂、需要考虑各种不利情况下多种荷载组合的结构稳定性分析。

［1］王 刚，陈 杨，张建民.大圆筒结构倾覆稳定分析的有限元法［J］.岩土力学，2006，27(2):238-241.

［2］肖 忠，王元战，及春宁，等.筒型基础防波堤稳定性有限元数值分析［J］.土木工程学报，2009，42(7):119-125.

［3］XIAO Zhong，WANG Yuan-zhan，Chen Xi.Stability analysis of semi-circular breakwater on soft foundation considering cyclic weakening effect［C］∥Proceedings of Chinese-German Joint Symposium on Hydraulic and Ocean Engineering.2010:587-595.

［4］王元战，张连丽，商 丹，等.倒T 型导管墙桩基防波堤稳定性简化计算方法［J］.岩土力学，2012，33(6):1839-1844.

［5］邱 驹.港工建筑物［M］.天津:天津大学出版社，2002.

［6］郑颖人，赵尚毅，张鲁渝.用有限元强度折减法进行边坡稳定分析［J］.中国工程科学，2002，4(10):57-61.

［7］赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24(3):343-346.

［8］刘金龙，栾茂田，赵少飞，等.关于强度折减有限元方法中边坡失稳判据的讨论［J］.岩石力学，2005，26(8):1345-1348.

［9］马建勋，赖志生，蔡庆娥，等.基于强度折减法的边坡稳定性三维有限元分析［J］.岩石力学与工程学报，2004，23(16):2690-2693.

［10］杨 萍，陈 洪.对强度折减法中折减系数的讨论［J］.四川建筑科学研究，2010，36(4):142-145.

［11］费 康，张建伟.ABAQUS 在岩土工程中的应用［M］.北京:中国水利水电出版社，2010.

［12］ZHENG Ying-ren，TANG Xiao-song，ZHAO Shang-yi，et al.Strength reduction and step-loading finite element approaches in geotechnical engineering［J］.Journal of Rock Mechanics and Geotechnical Engineering，2009，1(1):21-30.

［13］陈可文，潘海琳.基于强度折减有限元法的边坡稳定性计算［J］.黑龙江水专学报，2010，37(3):56-58.

［14］胡安峰，陈博浪，应伟宏.土体本构模型对强度折减法分析基坑整体稳定性的影响［J］.岩石力学，2011，32(2):592-597.

［15］JTJ 213-98，海港水文规范［S］.北京:人民交通出版社，2000.

［16］WANG Yuanzhan，ZHU Zhenyu.An approach to stability analysis of embedded large-diameter cylinder quay［J］.China Ocean Engineering，2002，16(3):383-393.

［17］周连有，李开元.天津港地区采用大圆筒结构设计方案研究［J］.港工技术，2009，46(6):18-22.