长江河口理论最高和最低潮面计算和应用
2013-11-22林唐宇朱建荣
林唐宇,朱建荣
(华东师范大学 河口海岸学国家重点实验室,上海 200062)
潮汐由不同周期的分潮组成,分潮位相的变化可导致潮位的变化,产生理论最低和最高潮面。理论最低、最高潮面的定义为:由主要分潮组合所得的理论上可能最低、最高的潮高[1]。它具有局地变化的特性,通常利用潮位站实测资料经调和分析后得到,类似于海图深度基准面。过去常采用手工计算,计算量大,精度较差,且只能逐点计算,所计算区域必须有长期的潮位站资料。随着计算机的普及,利用计算机计算理论最高最低潮面逐渐成为主要方法。吴华林等[2]用Matlab 语言实现了理论最低潮面的计算,利用1977年实测长江口潮位资料计算获得的调和常数,计算了长江口10 个验潮站的不同深度基准面值。钟华[3]选取长江口17 个验潮站,计算了理论最低潮面,采用GIS 技术实现了局部区域不同基准面之间的转化。航行海图水深是基于理论最低潮面给出的,以保障落潮期间航行的安全,海堤的设计需要理论最高潮面作为最基本的依据,而它们的计算需要潮汐的正确计算。因此,研究理论最低、最高潮面具有重要的理论和应用意义。
本文应用ECOM_si 海洋数值模式,计算长江河口及其邻近海域水位随时间变化,利用T_Tide[4]进行调和常数计算,给出主要分潮的调和常数,计算理论最高、最低潮面。2009年长江河口进行了一次较系统的地形测量,但仅取得理论深度基面的资料。理论深度基面的水深资料对航行是有用的,但对数值模式因不在统一基面上是不能使用的。作为应用之一,本文将之转为在85 国家高程基面上,使数值模式能应用这批较新的实测资料。
1 数值模式的设置和验证
1.1 数值模式的设置
本文采用应用和改进的三维数值模式ECOM-si,该模式已长期应用于长江口水动力过程和盐水入侵等方向的研究,并取得诸多成果[5-10]。
模式采用水平曲线非正交网格,范围包括整个长江河口、杭州湾和邻近海区,上游边界设在长江枯季潮区界大通,外海开边界东边到124.5°E 附近,北边到33°N 附近,南边到28°N 附近(图1)。对长江河口区域,包括南北支分汊口和深水航道工程区域的网格进行局部加密,较好地拟合了岸线和导堤。口内网格分辨率为100 至500 m 不等,口外网格较疏,分辨率最大为10 km 左右。垂向采用σ 坐标,均匀分为5 层。时间步长取40 s。长江河口区域浅滩较多,模式运用干湿判别法实现潮滩移动边界的模拟,临界水深取0.2 m。
模式地形采用2008年岸线及水深资料。外海开边界由潮位驱动,考虑16 个分潮(M2,S2,N2,K2,K1,O1,P1,Q1,U2,V2,T2,L2,2N2,J1,M1,OO1),由各分潮调和常数合成得到,资料由全球潮汐数值模式NAOTIDE 计算的结果得到,初始水位和流速取零且考虑径流量和海表面风应力的作用。
1.2 模式验证
由于计算理论最高、最低潮面都是从潮位出发,因此模式是否能够准确的模拟潮位是理论最高、最低潮面计算准确与否的关键。本文应用ECOM_si 模式已在长江河口作了大量的验证[5-10],模式计算的水位、流速流向和盐度与实测资料吻合良好。为节省篇幅,本文仅给出长江河口2009年潮位的验证结果,潮位站分布见图2。永隆沙、崇西、堡镇、南门、马家港、横沙潮位站潮位站资料为实测2009年逐时资料,中浚站采用2009年潮汐表潮位资料。考虑大通实测的径流量和崇明东滩实测风况随时间的变化。

图1 模式计算区域和网格Fig.1 The model domain and grids
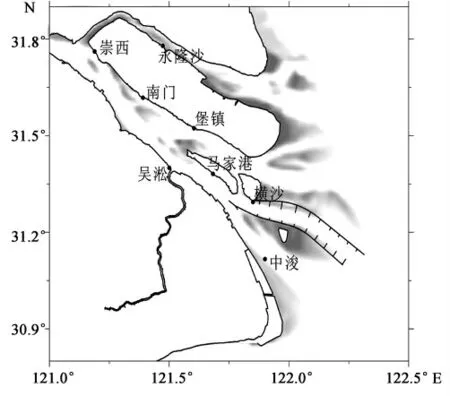
图2 验证潮位站分布Fig.2 Distribution of tidal station in the Yangtze Estuary for validation
图3 仅给出2009年2月1 ~15日潮位站水位验证情况,其余时段不再赘述。从图中可以看到,模式的水位模拟值与潮位站实测值吻合良好。潮位站分散分布于长江口,这表明模式能准确地模拟出长江口各处的水位变化。
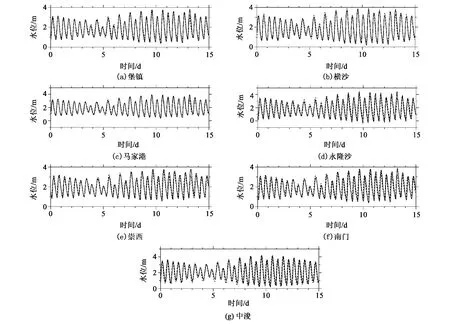
图3 2009年2月1 ~15日实测水位与模拟值对比(实线为实测数据,虚线为模式计算值)Fig.3 Comparison between the elevations observed and simulated from 1st Feb to 15th Feb in 2009 (real lines represent the observed and dashed lines repr-esent the simulated)
2 理论最低、最高潮面的计算和应用
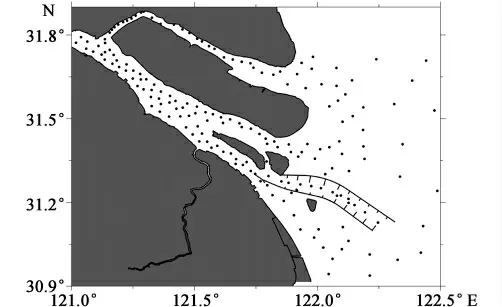
图4 模拟实验输出潮位点Fig.4 Tidal sites the model simulates
模式起始时间为2008年1月1日,计算时间为720 天,径流为实时大通流量,潮汐开边界由16 个天文分潮驱动。用于计算长江河口理论最低、最高潮面的模式输出点如图4 所示,共计184 个。北支水浅,落潮时大部分潮滩出露,故输出点设置在河槽中。南支的输出点也基本设置在河槽中。
2.1 潮汐调和分析
采用由Pawlowicz 等[4]提供的T_Tide 潮汐调和常数计算软件对数值实验中输出点潮位序列经行数据处理。T_Tide 软件利用最小二乘法,通过潮位序列,拟合并计算出本文计算理论最高、最低潮面所需的11 个分潮(M2、S2、N2、K2、K1、O1、P1、Q1、M4、M6和MS4)的振幅和相位。目前该软件被普遍运用于潮汐分析,经验证,该软件对长时间序列的潮位分潮有很高的准确性。
2.2 程序化计算的实现
本文理论最高、最低算法参考《海道测量规范》(GB12317—1998)[11],利用Fortran 语言实现,计算方法如下:
以M2分潮为例,每一个分潮引起的潮位变化写成:

潮汐水位变化为所有分潮之和:

式(1)中,H 为振幅,σ 为角频率,g 为迟角;f 为潮汐分潮振幅的改正因子,称为节点因子,是一个时间函数,周期约为18.61年;V0+u 为订正角。调和分析中取年平均后,令R=fH,即R 为分潮的振幅。R、g 由T_Tide软件计算得出。式(2)为考虑11 个分潮的潮高表达式,一般可只用8 个主要分潮来计算,而长江口浅水分潮作用不可忽略,故计算中除了考虑8 个主要分潮,还考虑了3 个浅水分潮M4、M6和MS4。
令φK1=σK1t+(V0+u)K1-gK1,其它分潮也类似。根据潮汐平衡理论可推导得:
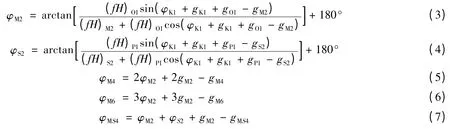
通过分潮的三角公式变化,可得:

其中,

故理论最高潮位表达式为:
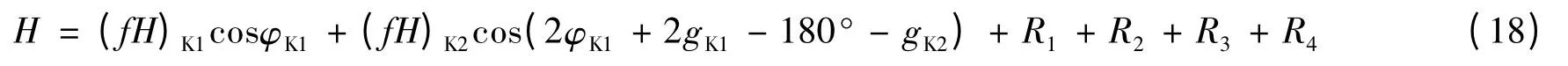
理论最低潮位为:

计算时,φK1从0°至360°变化,变化步长取为0.01°,H 的极大值即为理论最高潮面的量值,L 的极小值为理论最低潮面的量值,它们均相对于85 国家高程平均海平面。
2.3 算例与比较
以吴淞站为算例与吴华林[3]计算结果进行比对,如图5 所示。本文计算出的理论最低潮面为平均海平面以下170.953 cm,吴华林的结果为170.423 cm,两者几乎相同。
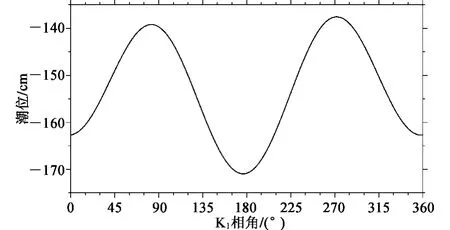
图5 吴淞潮位站理论最低潮面Fig.5 Theoretically lowest tidal level of Wusong tidal station
2.4 长江口理论最高、最低潮面
将数值模式计算的水位在输出点逐时输出,经T-tide 调和常数软件及上述算法计算,可得输出点理论最高、最低潮面。经插值后,分布见图6 和图7(基于平均海平面)。
理论最高、最低潮面的数值基本能反映局地潮汐作用的强弱。从图6 可见,北支理论最低潮面从口门处的-2.4 m 逐渐上升到上口的-1.5 m,口门处北侧理论最低潮面比南侧低约0.20 m。在南支,理论最低潮面从口门处的约-2.3 m 逐渐上升到南北支分汊口的-1.5 m,在浏河口区域相对较高,为-1.3 m;在南槽拦门沙区域,理论最低潮面从口门处的-2.3 m 逐渐上升到南北槽分汊口的-1.7 m,南侧低于北侧。在北槽,理论最低潮面从口门处的-2.2 m 逐渐上升到上口的-1.7 m。在北港,理论最低潮面从下游的-1.9 m 逐渐上升到上游的-1.6 m。南槽理论最低潮面低于北槽、北槽理论最低潮面低于北港。理论最高潮面的分布见图7,理论最低潮面低值处大致对应理论最高潮面的高值处,体现潮汐的极小值和极大值,但北支的理论最高潮面在中段,达到2.8 m。南槽的理论最高潮面大于北槽,北槽大于北港,在南支从口门处的2.5 m 向上游递减,至南北支分汊口约为1.6 m。

图6 理论最低潮面分布Fig.6 Distribution of theoretically lowest tidal level

图7 理论最高潮面分布Fig.7 Distribution of theoretically highest tidal level
2.5 应用
理论最低潮面最直接的应用在于航行图的给出,在河口海湾水域涨潮落潮水深变化大,故从航行安全考虑,水深必须以理论最低潮面作为基面给出。一些海图上水深标注基面为理论最低潮面,但并未给出具体量值,这对大区域数值模式是不能使用的,水深必须基于同一基面(如85 国家高程基面、吴淞基面等)。理论最高潮面对海堤的设计是至关重要的,考虑到风暴潮、海浪和洪水,海堤的设计高程必须大于理论最高潮面。
2009年长江河口作了一次较为全面的地形测量,但合作方提供的为基于理论最低潮面的地形资料(图8),需要转化为基于85 国家高程的资料才能应用。在计算水位时,笔者先用的地形资料是本课题组之前一直所采用的基于85 国家高程基面地形资料,计算出理论最低潮面与85 国家高程基面差值后,将合作方提供的水深资料转换成基于85 国家高程的新资料,为了尽量消除原资料不准确导致的错误,作者重复3 次上述步骤进行计算。图9 为应用本文理论最低潮面计算转化为85 国家高程基面后的地形分布。用该次地形资料和2003年地形资料计算了长江河口盐水入侵,崇头水文站的盐度过程线计算值与实测值吻合很好。

图8 2009年实测的基于理论最低潮面的水深分布Fig.8 Distribution of the depth based on the theoretically lowest tidal datum observed in 2009

图9 转换后基于85 国家高程的水深分布Fig.9 Distribution of the depth based on the geoid in the Huanghai Sea after conversion
3 结 语
应用ECOM_si 河口海洋数值模式,计算长江河口及其邻近海域水位随时间变化,利用T_Tide 调和常数软件计算得出潮汐的主要调和常数,根据《海道测量规范》(GB12317—1998)理论最低、最高潮面算法,得出长江河口理论最低、最高潮面的空间分布。
本文的数值模式应用于长江河口的海洋水动力和物理输运的研究,具有较高的计算精度。采用2009年全年长江河口7 个潮位站资料对潮位过程作了验证,吻合优良。应用的潮汐调和常数计算软件T_Tide 为国际公认的高精度计算程序,对长达近两年的逐时潮位资料进行调和常数计算,理论最低、最高潮面算法根据规范计算,并考虑长江河口潮汐特征,增加了三个浅水分潮M4、M6和MS4。
以往长江河口理论最低、最高潮面的计算,是基于潮位站实测资料。但因潮位站少,且空间分布不均,一些大范围水域内缺少潮汐调和常数资料,又因河口潮汐的空间变化大,故理论最低、最高潮面的给出存在困难、精度不高。本文采用数值模式,设计高分辨的网格,有效解决了上述不足,提升了理论最低、最高潮面的计算精度。将基于理论最低潮面的2009年长江河口实测地形资料,转化为基于85 国家高程的地形资料,使资料得到了充分应用。
[1]暴景阳,张明亮,唐 岩,等.理论最低潮面定义和算法的应用问题分析[J].海洋测绘,2009,29(4):1-8.
[2]吴华林,沈焕庭,吴加学.长江口海图深度基准面换算关系研究[J].海洋工程,2002,20(1):69-74.
[3]钟 华.长江口深度基准面转换的程序实现及其在滩涂资源调查中的应用[D].上海:华东师范大学,2010.
[4]Pawlowicz R,Beardsley B,Lentz S.Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE[J].Computers and Geosciences,2002,28:929-937.
[5]LIU G F,ZHU J R,WANG Y Y,et al.Tripod measured residual currents and sediment flux:Impacts on the silting of the deepwater navigation channel in the Changjiang Estuary[J].Estuarine,Coastal and Shelf Science,2010,73:210-225.
[6]CHEN B R,ZHU J R,FU L H.Formation mechanism of the freshwater zone around the Meimao Sandbank in the Changjiang Estuary[J].Chinese Journal of Oceanology and Limnology,2010,28(16):1329-1339.
[7]WU H,ZHU J R,CHOI B H.Links between saltwater intrusion and subtidal circulation in the Changjiang Estuary:A modelguided study[J].Continental Shelf Research,2010,30:1891-1905.
[8]项印玉,朱建荣,吴 辉.冬季陆架环流对长江河口盐水入侵的影响[J].自然科学进展,2009,19(2):192-202.
[9]朱建荣,傅利辉,吴 辉.风应力和科氏力对长江河口没冒沙淡水带的影响[J].华东师范大学学报:自然科学版,2008(6):1-8.
[10]LI L,ZHU J R,WU H,et al.A numerical study on the water diversion ratio of the Changjiang Estuary during the dry season[J].Chinese Journal of Oceanology and Limnology,2010,28(3):700-712.
[11]GB12317-1998,海道测量规范[S].北京:中国标准出版社,1998.
