深水无粘结柔性管抗拉伸层屈曲问题研究进展

杨 旭，孙丽萍，艾尚茂

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150076)

立管和海底管道系统作为海洋石油开发系统中的关键部分，承担着运输油气、钻井、注水等重要任务，被誉为“海洋石油生命线”。与其他管道产品相比，柔性管具有结构布置形式灵活、顺应性强、与平台耦合较弱、安装与回收成本低等优点，在挪威北海、巴西以及美国墨西哥湾的深海油气田中被广泛运用。我国南海油气资源储量丰富，绝大多数油藏处于深水、超深水区域。可以预见，深水柔性管在我国南海有着广阔的发展前景。

柔性管一般分为粘结(bonded)柔性管和无粘结(unbonded)柔性管两种形式。粘结柔性管，主要指立管内各层结构不能相互滑移，其制造长度因硫化工艺受到限制;而无粘结柔性管道则无此限制，长度可达几百米甚至几千米，且便于依用户要求而增减结构层的数目是目前柔性管的主要形式，被广泛应用［1］。这里所指柔性管为无粘结柔性管。

无粘结柔性管是多层复合管状结构物，一般按从内层到外层顺序包括内衬层(internal carcass)、内压防护层(internal pressure)、内锁压力层(pressure armor)、抗磨层(anti-wear tape)、抗拉层(tensile armor)、外保护层(outer sheath)，此外在一些层与层之间还存在用聚酯纤维(polymer)制作的中介保护层。柔性管各层的英文名称、材料、功能如图1 所示。内衬层采用不锈钢材料制作，是由截面为S 型的连续长钢条经塑性成形制成的一种内部自锁柔性结构。该层是柔性管的主要支撑结构，承受内外部的径向载荷，防止立管因径向变形而发生塌陷等结构失效。内压防护层是由复合材料聚酯纤维制造的相对较薄的中介层，主要目的是防止内衬层和抗压层的移位，抵抗化学侵蚀，防止内外层结构互相影响。内锁压力层是由两条碳钢钢带沿着与管轴近90°方向缠绕而成的互锁结构层。该层可增强柔性管的内外压承载能力，且能够承受径向载荷，但是该层对轴向载荷和弯曲载荷的承载能力较弱。抗拉层是由两层轴对称的螺旋钢缆层制成，钢缆与轴向夹角为30°～55°，用以抵抗轴向拉力，防止管线断裂，不具备抵抗轴向压应力的能力。外保护层主要由复合材料制作，目的是防腐、防止内层磨损等［2］。柔性管结构形式复杂，在工作和安装过程中，会受到内外压、轴向拉力、弯矩、扭矩等多种载荷，存在着压溃、屈曲、疲劳、屈服等多种失效形式，这都为柔性立管设计带来了极大的挑战。目前，柔性管的设计和建造技术基本被法国的Technip 公司、英国Wellstream 公司和丹麦NKT 公司垄断，国内对于柔性立管的设计制造基本处于空白［3］。

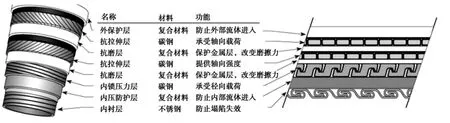
图1 柔性管各层结构名称、材料、功能Fig.1 Materials，functions and names of flexible pipe cross-section's layers

深水柔性管在安装或工作工况中，在弯曲点会受到弯矩和水压的共同作用，抗拉层螺旋钢缆会受到轴向压应力作用，产生屈曲失效。随着工作水深的增加，抗拉伸层钢缆屈曲成为柔性管的重要失效形式。柔性管螺旋钢缆受压屈曲，包括径向屈曲或者侧向屈曲两种形式，如图2 所示。其中径向屈曲指的是钢缆遭到破坏凸出圆柱表面，因为破坏形式形似鸟笼，又被称为“鸟笼现象”。侧向屈曲指的是钢缆沿着圆柱表面发生横向偏移［4-5］。鸟笼现象和侧向屈曲最早是20 世纪90年代末期在挪威海域的一个1 700 m 水深的柔性管道铺设项目中被发现的。屈曲分析一般考虑两种情况，其一为管道外侧未遭到破坏，抗拉层螺旋钢缆需承受外部水压力，称为干燥环境(dry annulus condition);当管道遭到破坏，螺旋钢缆已经与海水接触，则螺旋钢缆不再受到外部水压影响，称为湿环境(wet annulus condition)，其中干燥环境下更易进入材料塑性变形阶段［6-7］。

螺旋钢缆屈曲失效涉及多种非线性结构问题，具有重要的研究意义。近年来国外许多学者致力于对该问题的研究，取得了许多成果。这里从数值模拟和试验两方面介绍国外的研究现状及其有待解决的主要问题，希望可以为国内柔性管的发展提供参考。

图2 柔性管抗拉层螺旋钢缆的受压屈曲Fig.2 Radical buckling failure

1 数值模拟研究进展

数值模拟的主要意义在于将数值结果与已有试验进行对比，寻找一种准确成熟的方法以替代昂贵的试验，分析影响抗拉层屈曲的主要因素，为建立柔性立管设计规范提供参考。当前基本采用非线性有限元法对该问题进行仿真模拟。该问题的主要难点在于:第一，螺旋钢缆是特殊的结构形式，用传统的欧拉伯努利梁模型或实体模型难以准确模拟。第二，屈曲和后屈曲问题属于大变形小应变问题，涉及到几何非线性。第三，结构屈曲后，结构可能处于塑性阶段，同时柔性管还存在迟滞效应，属于材料非线性问题。第四，需要模拟螺旋钢缆之间的接触和抗拉层与耐磨层及其他层之间的接触，这属于接触非线性。此外，目前的计算机能力还不足以应付如此大规模的计算，计算效率也是需要重点考虑的因素。

针对上述问题，一部分学者试图在非线性有限元的基本框架下改进已有单元类型或建立新单元类型，来代替传统的梁单元或实体单元，找到一种快速、稳定、准确的求解方法。另一部分学者则运用经典的非线性有限元法，以传统单元模型进行建模，分析抗拉伸层螺旋钢丝的屈曲及后屈曲性能。

对于新单元类型的研究大多处于理论探索阶段，目前的研究对很多次要问题进行了假设，取得了一定的研究成果，但还不能广泛应用于工程实际。Zhu Z H［8］等人运用三维曲梁单元模拟螺旋层钢缆，该单元为三节点单元，应变-位移基本方程基于Love 的经典理论［9］，即:

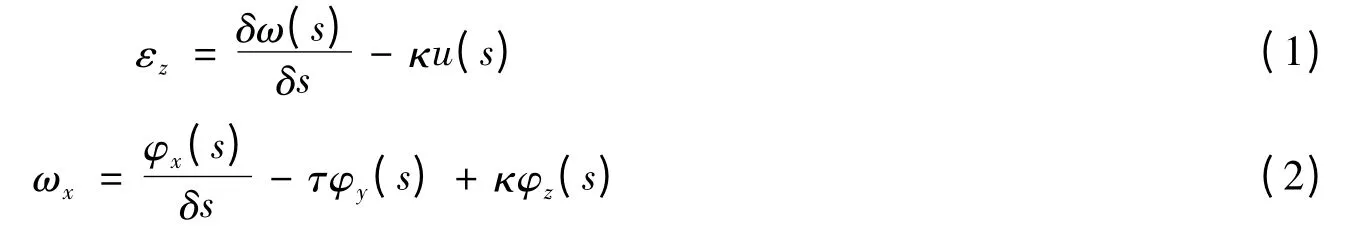
假设εz和ωz在单元内随Z 轴位移线性变化，以此有效避免了剪力锁定现象，其坐标系沿着螺旋线建立。作者将分析结果与ANSYS 软件结果进行了对比，结果较为接近。Ginema［10］等人应用曲梁单元，运用差分平衡方程，同时将坐标转化为笛卡尔坐标系，对螺旋构件进行了解析推导，获得了较好的结果。Rodigero P 等人在Zhu［8］的基础上，对三维曲梁进行了改进，使其可以模拟扭转，其法向和副法向位移模式如下:

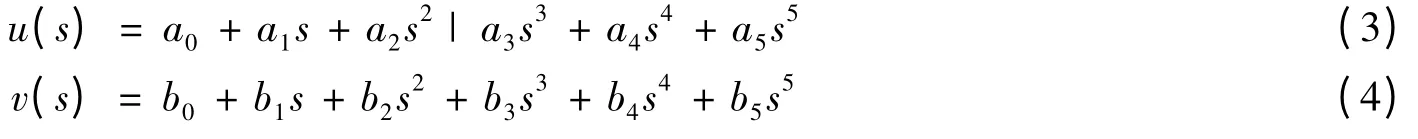
该三节点单元刚度矩阵达到1 200 行，但仅用很少量的单元(20 ～50 个)即与ANSYS 软件运用1 000 个三维梁单元所得结果类似［11］。该文没有对单元进行屈曲分析，但单元能够模拟轴向压力作用，因此可以对其进行后续研究以获得屈曲载荷和后屈曲性能。

Saevik S 等人［12-14］在该方面进行了大量研究:其对螺旋钢缆的模拟基于非线性细长杆理论，采用Green应变和第二Kirchoff 应力进行分析，坐标系采用沿螺旋线布置的直角坐标系，单元如图3 所示，坐标系如图4所示。

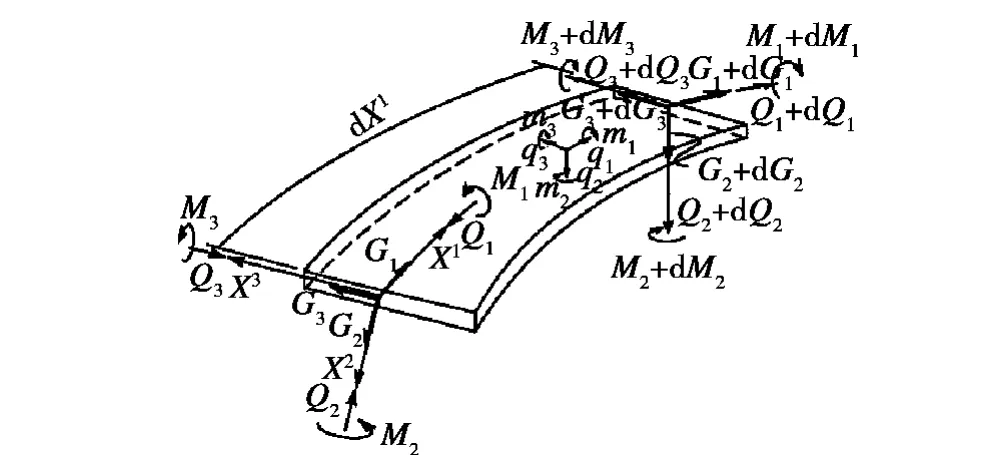
图3 曲梁单元微段Fig.3 Infinitesimal curved beam element

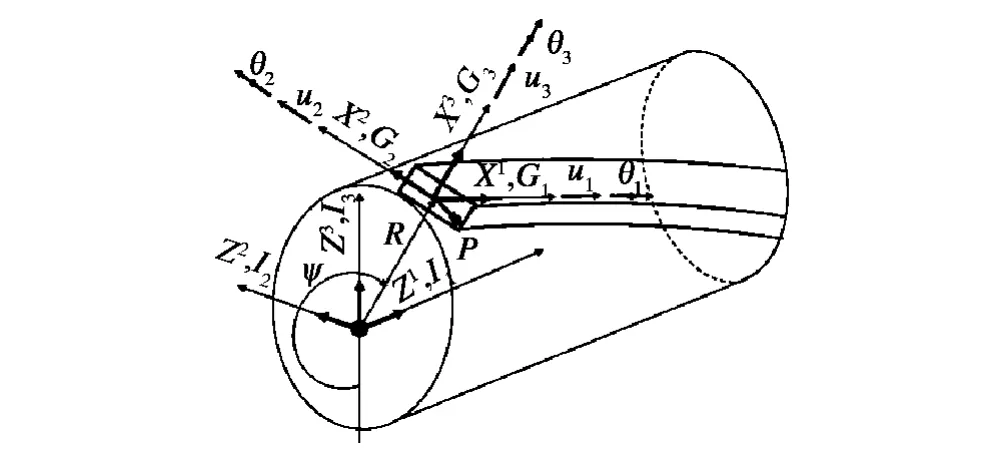
图4 曲梁单元坐标系Fig.4 Curvilinear beam coordinate systems

将所需的参数用柔性立管截面中心点的位移与应力表示，抗拉层螺旋钢丝的Green 应变可以表示为:

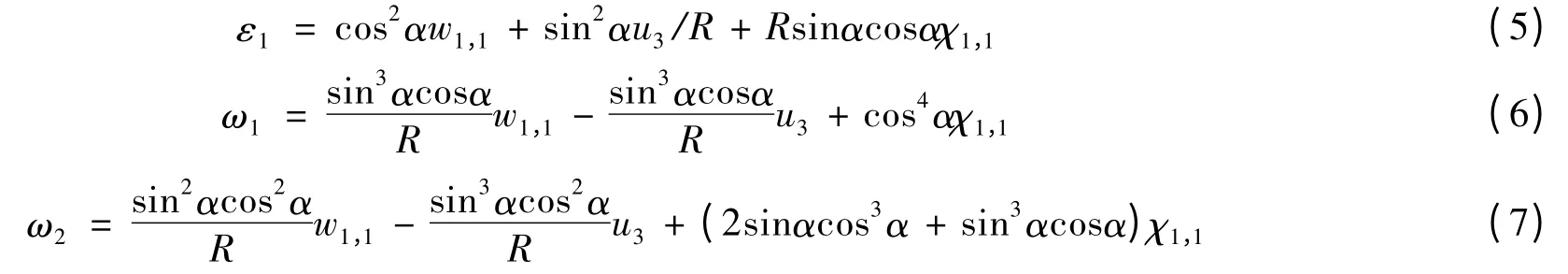
式中:下脚标1 表示对于坐标轴1 的偏导，w1和χ1为管中心截面对应的轴向和扭转自由度。作者运用轴对称单元来模拟未受弯矩之前的柔性立管内层结构，用接触算法和曲梁单元模拟抗拉层。这样可以减少计算量。而对于受到弯曲后的结构用夹层梁单元和增加相互接触自由度的标准三维梁单元，运用两种单元对柔性管进行了应力分析，分析结果得到两者都能很好地模拟螺旋层应力，但应用夹层梁单元模型计算效率更高。上述研究已可以较好地模拟柔性立管的各种载荷，但还没有对屈曲问题进行分析，后续工作主要是对矩阵特征值进行求解和进行屈曲后结构分析。

Zhimin T［6］等人运用能量法变分原理对螺旋钢缆屈曲进行了解析解计算，其所用的基本方程式为:

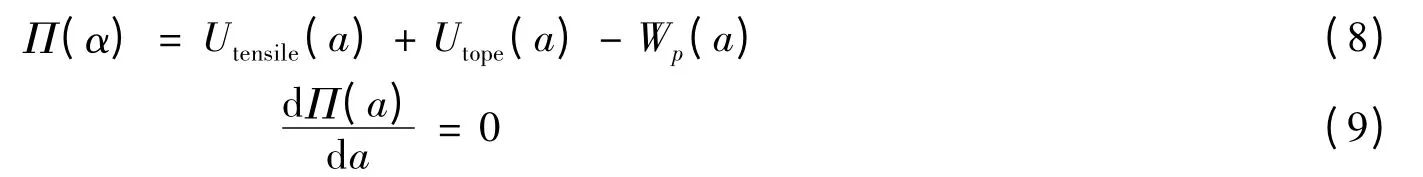
式中:a 为钢缆应变，Π 为系统总能量，Utensile为螺旋钢缆变形能，Utape为抗磨层产生的变形能，W 为所做的功。通过该方程组得到了轴向压力—应变平衡曲线，其计算结果如图5 所示。该文只给出了定性分析曲线，并没有给出具体的结果和推导过程。从中可以看出干燥环境和湿环境下的临界载荷有明显的差异。该文还指出当管道发生弯曲时，其平衡路径会变得相对光滑。

Niels H 和Anders L［15］假设柔性管弯曲半径不变，忽略摩擦力以及扭转力，运用力的平衡方程以及几何非线性理论对抗拉层进行模拟。他们运用Cauchy 应力表示应力，将一根螺旋钢缆作为一个单元推导出其解析解。文章将一根柔性管作为算例进行了侧向屈曲分析，结果如图6 所示［15］。该文采用了诸多假设，同时考虑管道仅发生侧向屈曲而不发生鸟笼响应，具有一定局限性。

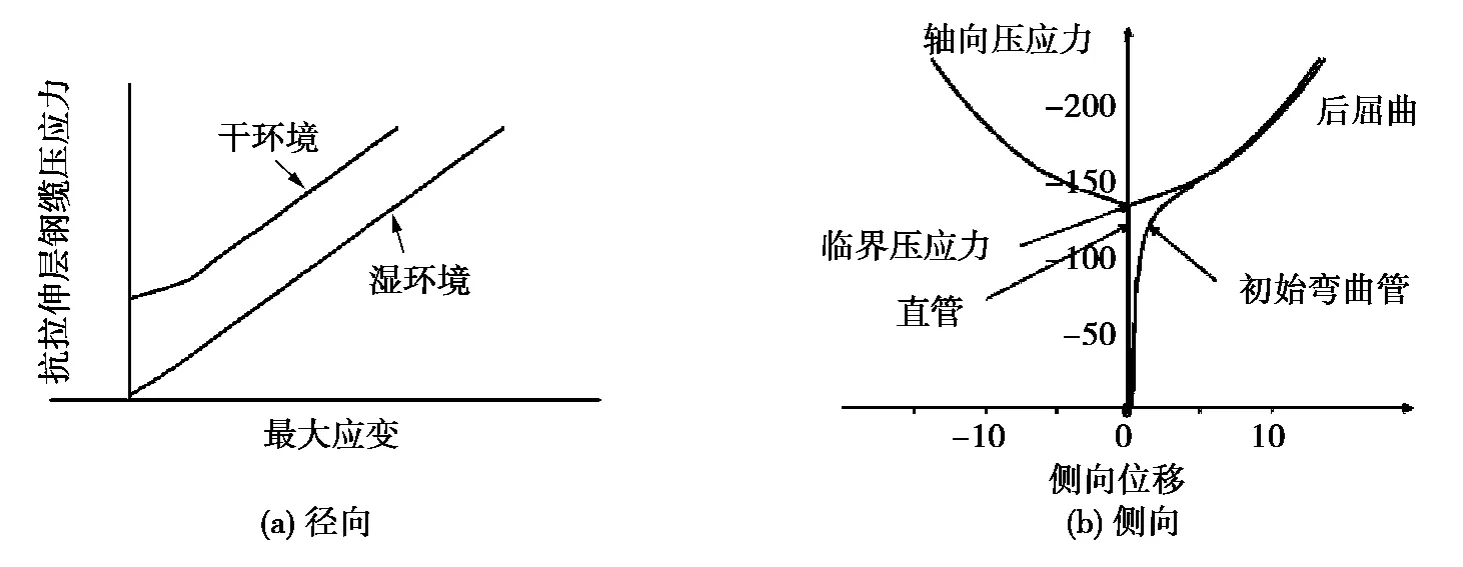
图5 屈曲压载荷应变平衡曲线Fig.5 Equilibrium paths

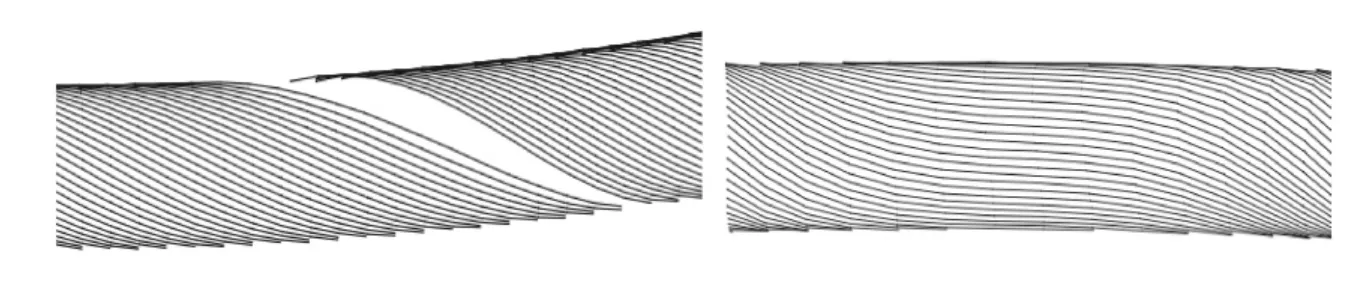
图6 侧向屈曲失效结果Fig.6 Numerical simulation results of lateral buckling mode

由于新单元类型尚不成熟，一些学者采用ABAQUS 或ANSYS 等成熟的有限元软件，运用梁单元或实体单元建立模型进行分析，对柔性管屈曲问题进行模拟。其主要侧重点在于接触单元的模拟和如何选择方法缩短计算时间同时保证计算精度。

Zhang Y［16］较早进行了这方面的研究，介绍了柔性管局部结构设计的一些问题，应用有限元法建立了一个预测鸟笼效应的螺旋钢缆模型。该文采用了传统的三维梁单元，对分布在两个抗拉层的两条螺旋钢缆进行了建模，采用线性方法计算了该模型的一阶屈曲载荷;由于采用线性模型，并不能进行后屈曲性能分析。Bectarte［17］等描述了螺旋钢缆屈曲的机理，给出了一个计算模型。Fabio P［18］等描述了一个2 500 m 水深9.13英寸柔性输油管工程实例的设计过程，指出了预防鸟笼效应的设计要点。提出要防止鸟笼现象，一个有效的方法是提高抗拉层厚度，但这种方法对预防侧向屈曲效果不大;因此要完整地考虑抗拉层螺旋钢缆的屈曲问题，主要设计参数应是螺旋钢缆截面的几何形状、尺寸以及螺旋角的大小。

图7 柔性管有限元模型Fig.7 FEM model of flexible pipe

Jose R［19］等运用ANSYS 软件建立了如图7 所示的柔性管有限元模型。在这个模型中，内部的内衬层和内锁压力层被模拟为SHELL 单元，螺旋钢缆被模拟为三维直梁单元;在这个模型中考虑了材料非线性、几何非线性和接触问题。文中以一个2.5 m 长4 英寸的柔性管作为模型，网格数达到了121 394 个，自由度更达到391 128 个;文中并未提及计算时间和效率，但是考虑到网格数和强非线性，计算效率可想而知。作者将有限元模型计算结果与试验结果进行对比，轴向位移、轴向缩短距离拟合较好，但表示侧向屈曲的扭转角有一定差距，具体对比结果见图8。

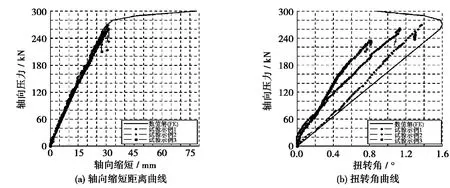
图8 轴向缩短距离、扭转角与轴向荷载关系曲线Fig.8 Applied axial compression vs. axial shorting and twist angle

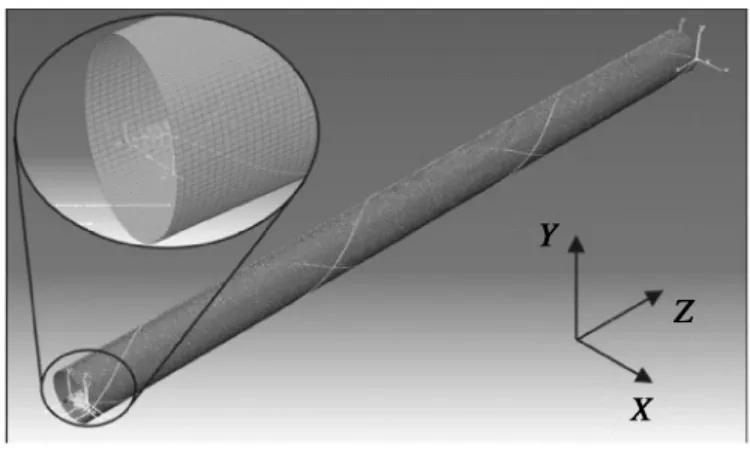
图9 柔性管抗拉层钢缆有限元模型Fig.9 FEM model of tensile armor wires

Vaz M A［7］等建立了一个柔性管三维非线性有限元模型，如图9 所示。在这个模型中，运用直梁单元模拟抗拉层螺旋线，运用弹性支持来模拟抗拉层内外的各层结构，用罚函数接触算法模拟两螺旋线之间的接触，在两螺旋线间建立了一个圆柱形表面单元，用以确立接触。运用ABAQUS 软件进行了有限元分析，该文只考虑了几何非线性，并没有考虑柔性管塑性变形。作者认为柔性管抗拉层钢缆的屈曲形式主要取决于接触摩擦系数和外压力，外压力、摩擦系数与计算实例的临界载荷关系如图10 所示。作者将其分为A、B、C 三个区。其中A、B 区为侧向屈曲，C 区为鸟笼屈曲。图11 和图12 为文中算例结果。其中图11 摩擦系数0.4，外压力为0 MPa;图12 摩擦系数为0.01，外压力分别为6 MPa 和15 MPa。

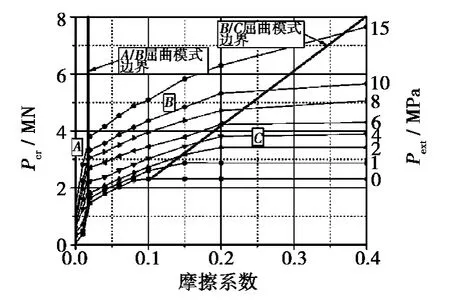
图10 摩擦系数、外载荷与临界载荷曲线Fig.10 Instability load vs.friction coefficient and external pressure

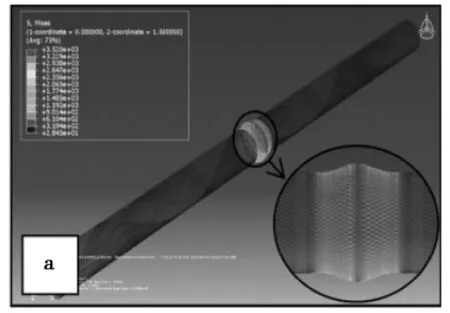
图11 柔性立管屈曲应力分析(外压0 MPa，摩擦系数0.4)Fig.11 Riser configuration (friction coefficient 0.4 and external pressure 0 MPa)

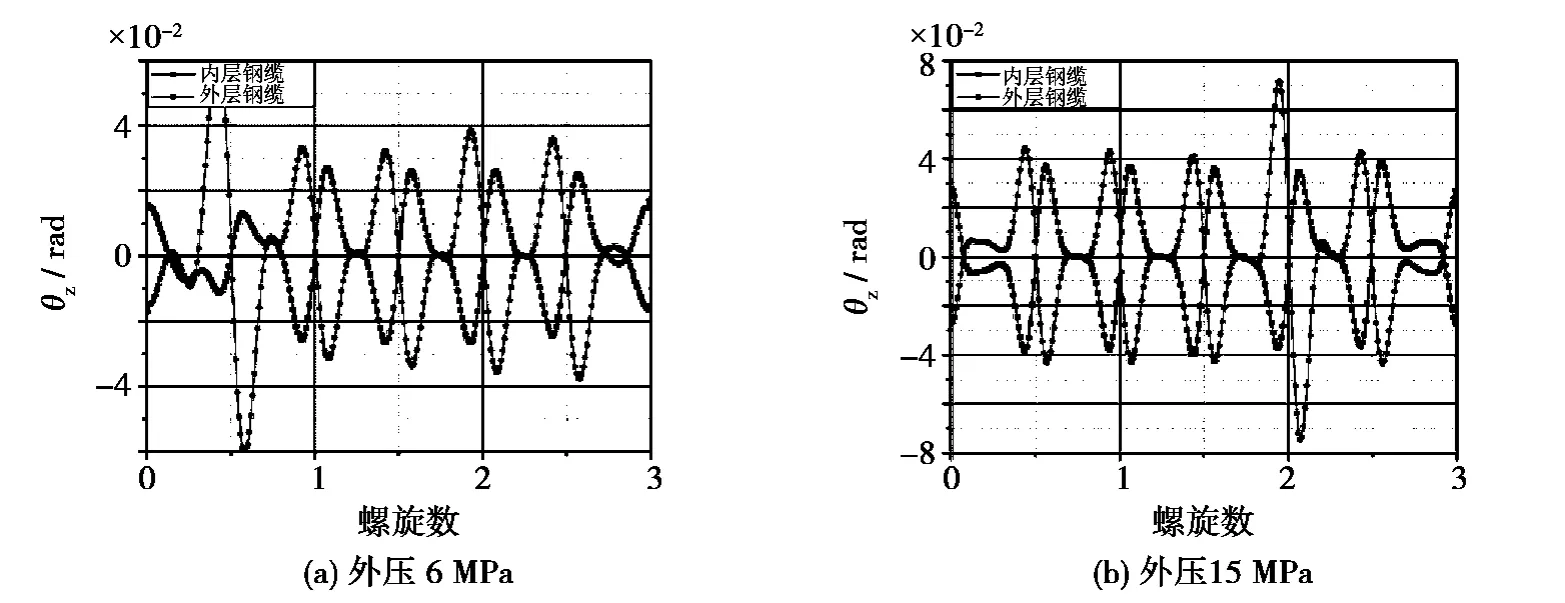
图12 侧向屈曲后钢缆转角Fig.12 Rotation around Z-axis as a function of model length with external pressures equal to 6 MPa/15 MPa

2 试验方法研究进展

对于鸟笼效应和侧向屈曲问题，国内外对于其数值模拟的研究还不够成熟。因此，当前广泛采用试验方法进行螺旋钢缆的屈曲校核，目的主要是在柔性管设计中确定其是否会屈曲失效以及失效后结构响应。现今的试验方法均为全尺度试验，主要分为三类，一是海上DIP(deepwater immersion performence)试验;二为压力舱(pressure chamber)试验;三是机械性能试验。其中，DIP 试验与真实工况最为相近，试验结果也最为准确，但其需要水下机器人和海上船舶，成本十分高昂;所需实验设备也不是一般的研究机构所拥有的。目前只有柔性管制造设计公司和大型石油公司进行过这类试验。压力舱试验成本大约为DIP 试验的1/5 到1/10，但需要大型密封舱等特殊实验设备。目前国外的主要研究集中在找到一种合适的压力舱试验方法，达到与昂贵的DIP 试验相同的准确性。对于一些没有压力舱设备的实验室，机械性能试验是对柔性管研究的首选试验，采用等效力的方法运用机械装置模拟海底压力和弯矩，这样可以大幅度减少成本，但机械性能试验并不能完美模拟海底工况，国内外研究机构对其准确性还持保留态度。值得一提的是，上面三种试验均为全尺度试验，目前国内外大型研究机构还没有进行柔性管缩尺比模型试验。这是由于柔性管结构形式复杂，生产困难，要想制造完美模拟柔性管力学性质的模型十分困难。

Zhimin T［6］分别对4 ～6 英寸柔性管做了DIP 试验和压力舱试验，密封舱结构如图13 所示，试验结果表明柔性管局部屈曲主要与水深、弯曲半径、管道内径、螺旋钢缆尺寸和布置角度、抗磨层厚度五个因素有关。DIP 试验被认为是近年来柔性立管的权威性试验，被很多学者用来与数值模拟进行对比。Roberto R［20］等人描述了柔性管机械性能试验的详细试验方案和试验结果，应变片的贴法如图14 和图15 所示，图16 为试验装置图。该试验并没有进行柔性管压载荷试验，不过其试验过程、试验装置等与柔性管受压屈曲试验类似，可以提供参考。

图13 柔性管压力舱试验安装Fig.13 Pressure chamber and test setup

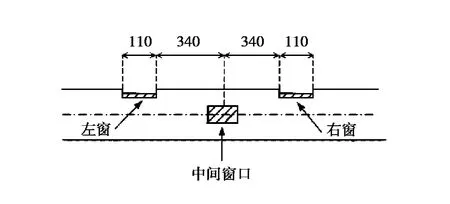
图14 柔性管机械性能窗口简图Fig.14 Schematic view of the windows

巴西的Jose R［19］等人在COPEE/UFRJ 实验室对4 英寸柔性管进行了机械性能试验，试验结果见表1。试验结果中法向应力和副法向应力都随着轴向压力的增大而不断增大，并呈现出两段直线型的特性。NKT公司的Niels H［15］等对5 m 长6 寸的柔性管进行了机械性能试验。Technip 公司Philippe S［21］等详细阐述了各种柔性管试验的优缺点和注意事项，提供了柔性管试验的选择依据，并且描述了2010年初Technip 公司在美国墨西哥湾所做的水深达3 000 m 的DIP 试验。试验中水下机器人拍摄的照片如图17、屈服形式如图18 所示。该试验是成本较高，试验精度最高的超深水DIP 试验，试验结果被作为经典算例，广泛用于对比数值模拟结果。

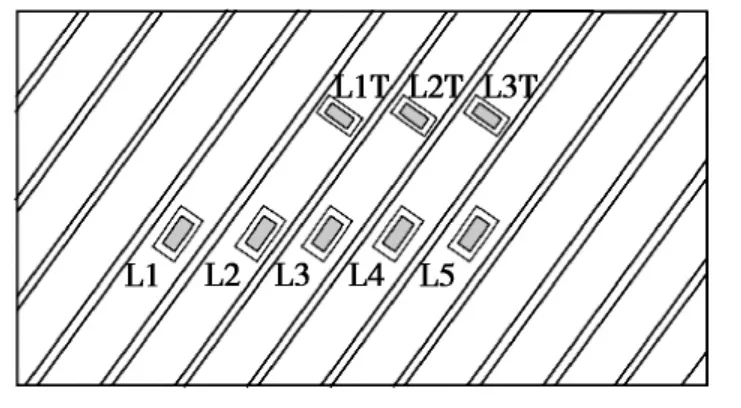
图15 左窗口区应变片粘贴位置Fig.15 Strain gages used in the left window

图16 柔性管机械性能试验的试验装置Fig.16 View of mechanical test

表1 试验数据Tab.1 Test results of 4”flexible pipe

图17 DIP 试验水下拍摄情况(2 600 m 水深)Fig.17 DIP test of the 11″ Sour line at water depth of 2 600 m

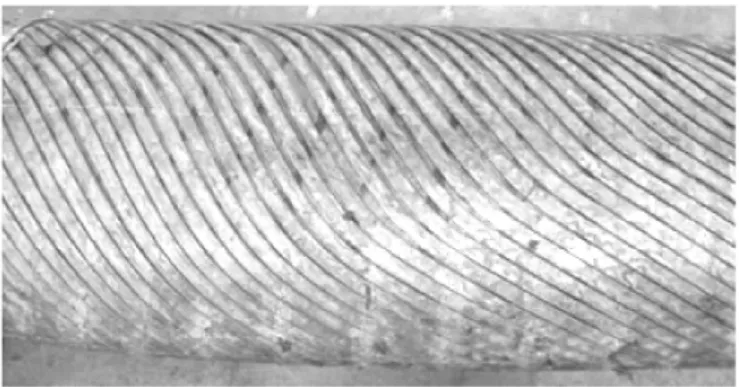
图18 DIP 试验柔性管侧向屈服破坏形式Fig.18 Failure pattern of sweet flooded sample in DIP test

3 结 语

柔性管抗拉层的螺旋钢缆受压屈曲是柔性管设计中的重要问题，国内对于该问题的研究基本为空白。总结了近15年来国外对于该问题的研究成果，可为我国柔性管研究提供参考。

目前的研究主要有试验、数值模拟两种方法;工程上仍以试验研究为主。试验方法为全尺度试验，包括DIP 试验，压力舱模拟试验和机械性能试验三种。目前DIP 试验较成熟，但试验成本过高;压力舱试验和机械性能试验的结果精度还在研究中。在以后的研究中，开发一种合适的压力舱或机械性能试验方案代替昂贵的DIP 试验将是一个热点课题。

数值模拟方法大多运用非线性有限元法，其研究主要为两方面:一是对新型有限元单元类型的理论探索，当前已经获得了一些适用于螺旋结构的单元类型，取得了良好的计算效率和结果精度;二是应用传统单元类型进行建模，已出现多种建模方法和算例，并确定屈曲失效主要与立管半径、抗拉层钢缆螺旋角、抗拉层钢缆截面属性、作业水深以及保护层厚度等因素有关。发展一种快速准确的数值模拟分析方法始终是柔性管屈曲问题的研究难点。

从工程应用角度来看，结合试验和非线性有限元法的研究，确定主要参数与屈曲失效的关系，得到经验公式或完善相关规范等也是亟待解决的问题。

［1］周 佳.无粘结柔性管的非线性迟滞特性研究［D］.哈尔滨:哈尔滨工程大学，2012.

［2］Alfredo G N，Clovis A M.A comparative buckling study for the carcass layer of flexible pipes［C］//Proceedings of the ASME 28 th International Conference on Offshore Mechanics and Arctic Engineering (OMAE).2009:1-10.

［3］李 鹏，李 彤，张洪凯，等.深水FPSO 柔性管［J］.中国造船，2010(51):379-385.

［4］Anderson B C，Carlos L，Lea T，et al.Recent research on the instability of flexible pipe's armours［C］//Proceedings of 17thInternational Offshore and Polar Engineering Conference.Lisben:ISOPE，2007:1026-1032.

［5］Bectarte F，Coutarel A.Instability of tensile armour layers of flexible pipes under external pressure［C］// Proceedings of the 23rd OMAE. Vancouver:ASME，2004:1-6.

［6］Zhimin T，Cobie L，Terry S，et al.Behavior of tensile wires in unbonded flexible pipe under compression and design optimization for prevention［C］∥Proceedings of 25th OMAE.Hamburg:ASME，2006:1-8.

［7］Vaz M A，Rizzo N A S.A finite element model for flexible pipe armor wire instability［J］.Marine Structures，2011(24):275-291.

［8］Zhu Z H，Meguid S A.Analysis of three-dimensional locking-free curved beam element［J］.International Journal of Computational Engineering Science，2004(5):535-556.

［9］Love A E H. A Treasite on the Mathematical Theory of Elasticity［M］.4thEdition，New York:Dover，1944.

［10］Gimena L，Gimena F N，Gonzaga P.Structural analysis of a curved beam element defined in global coordinates［J］.Engineering Structures，2008(30):3355-3364.

［11］Rodrigo P，Clovis A M.A Three-dimensional curved beam element for helical components modeling［C］∥Proceedings of 30th OMAE.Rotterdam:ASME，2011.

［12］Saevik S.A finite element model for predicting stresses and slip flexible pipe armouring tendons at bending gradients［J］.Computers and Structures，1993(46):2.

［13］Saevik S，Giertsen E，Olsen G P.A new method for calculating stresses in flexible pipe tensile armours［C］∥Proceeding of 17thOMAE.Lisboa:ASME，1998.

［14］Saevik S.Theoretical and experimental studies of stresses in flexible pipes［J］.Computers and Structures，2011(89):2273-2291.

［15］Niels H，Anders L，Jens H A.On lateral buckling failure of armor wires in flexible pipes［C］∥Proceedings of 30thOMAE.Rotterdam:ASME，2011.1-10.

［16］Zhang Y，Chen B，Hill T，et al.State of the art analytical tools improve optimization of unbonded flexible pipes for deepwater environments［C］∥Proceedings of 2003 Offshore Technology Conference.2003:1-10.

［17］Bectarte F，Coutarel A.Instability of tensile armour layers of flexible pipes under external pressure［C］∥Proceeding of Deep Offshore Technology. 2005.

［18］Fabio P，Judimar C，Terry S，et al.9.13inch gas export flexible pipe prototype development for ultra-deep water projects in the Brazilian pre-salt area［C］∥Proceeding of 29thOMAE.Shanghai:ASME，2010.

［19］Jose R M S，Paula F V，Carlos M，et al.An experimental and numerical study on the axial compression response of flexible pipes［C］∥Proceeding of 29thOMAE.Shanghai:ASME，2010.

［20］Roberto R，Clovis A M，Celso P P，et al.A case study on the axial-torsional behavior of flexible pipes［C］∥proceeding of 27th OMAE.Estoril:ASME，2008:4-5.

［21］Philippe S，Bectarte F，Henry A.Lateral buckling of armor wires in flexible pipes:reaching 3 000 m water depth［C］∥Proceedings of 30thOMAE.Rotterdam:ASME，2011:1-8.