超长离散信号聚类方法研究及其在潮型分类中的应用*
2013-11-21张立振玄春艳曹露洁
张立振,玄春艳,曹露洁
(1.中国海洋大学 数学科学学院,山东 青岛266100;2.中国海洋大学 工程学院,山东 青岛266100)
在实际工作中经常遇到聚类问题,关于这方面的研究已取得一些很有价值的成果[1-6]。对于短时信号的聚类,在医学等方面也有了很多的研究[7-8],例如用仪器测量心音[7]或者静息态功能磁共振成像[8]的数据均可以看作信号,但聚类方法仅限于将短时间内所得数据进行传统的聚类,并根据时频分析的结果来验证聚类的实际意义。
目前,关于超长离散信号的聚类研究很少见到,而如何快速高效地解决超长离散信号的聚类问题确实需要面对,例如全球有大约596个验潮站,每个验潮站都以1h为采样间隔测得海面的高度。根据这些数据研究验潮站的潮型以及平均潮差对于港口航道通过能力具有积极的意义[9],若将全球验潮站所处海域的潮型进行分类,考虑到日月地的周期变化规律,至少应该截取连续长度为期1a的数据才能合理、准确地得出结论。假如将每个验潮站在同一年中的24×365=8 760个有序采样值看成离散信号,这便属于典型的超长离散信号的聚类问题。
按照传统的聚类方法,自然是将每个验潮站同一年内得到的离散信号看成是8 760维空间中的一个点,共有596的点。根据通常两点间距离的定义,要计算8 760维空间中596个点中任意两点之间的距离,其计算量还是相当可观的。下面针对超长离散信号的聚类问题,给出一种全新定义两个离散信号之间距离的方法,以便快速有效地实现超长离散信号的聚类。然后,将新方法应用于世界各验潮站海面波动信号的聚类,绘出全球潮型分布图。
1 两道超长离散信号之间广义距离定义
1.1 长度为N 的超长离散信号空间到2L 维空间的映射(L≪N)
对于有限离散实信号:{x(kΔ)|k=0,1,2,…,N-1},可简记为


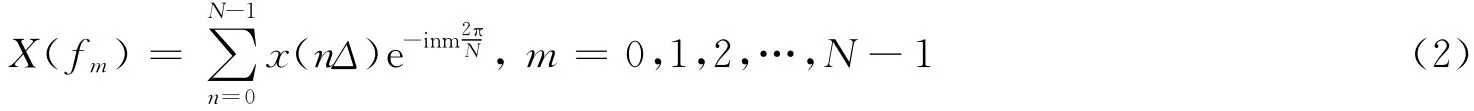
将X(fm)简记为Xm。由式(2)知为离散信号的平均值,所以X0只反映信号平均值的大小,并不包含任何波动的信息。又因为{xk}为实信号,所以Xm具有性质:

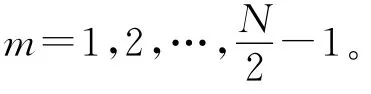
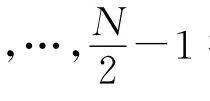
B)将选出的前L 项根据其下标按从小到大的顺序重新排列,得到数组:

式中,m1≤m2≤…≤mL。
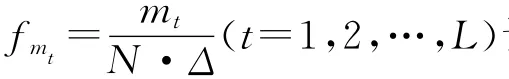

将式(4)中的数组(Xm1,Xm2,…,XmL)称为信号{xk}的L 主频谱;将式(5)中的数组(fm1,fm2,…,fmL)称为信号{xk}的L 主频率;这样每道长度为N 的离散信号{xk}在执行完上述三步后都有2L 元数组(Xm1,Xm2,…,XmL,fm1,fm2,…,fmL)与之对应。
为方便计,将长度为N 的离散信号构成的空间记为U;将数组(Xm1,Xm2,…,XmL,fm1,fm2,…,fmL)构成的2L 维空间记为V;建立从U 到V 的映射h:
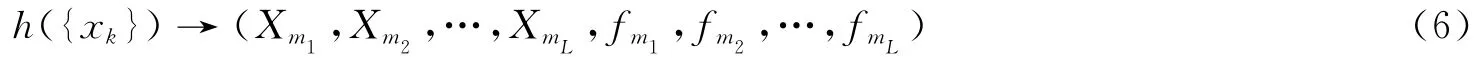
式中,(Xm1,Xm2,…,XmL)为信号{xk}的L 主频谱;(fm1,fm2,…,fmL)为信号{xk}的L 主频率。
现设有n道信号{xi,k|k=0,1,2,…,N-1},i=1,2,…,n,采样间隔均为Δ,长度皆为N。简记为{xi,k},k=0,1,2,…,N-1,i=1,2,…,n。根据式(6),信号{xi,k}(i=1,2,…,n)映像为
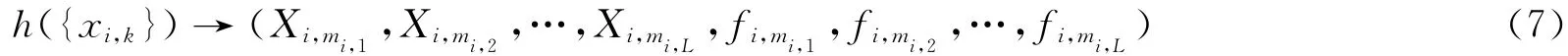
其中:
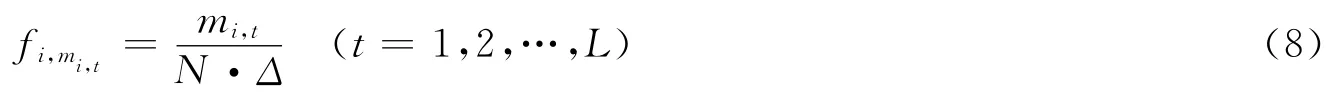
1.2 最小长度为N 的超长离散信号空间到2L 维空间的映射(L≪N)
实践中,除遇到具有相同采样间隔和相同长度的超长离散信号聚类问题外,还经常遇到具有相同采样间隔,不同长度的超长离散信号的聚类问题。例如,在前面提到的潮型聚类问题中,理想情况是截取全球所有验潮站同一年内的完整信号。但是,很可能有相当一部分验潮站在那一年只有9个月或10个月的测量数据。现设有采样间隔均为Δ,长度分别为N1,N2,…,Nn的n 道信号{xi,k|k=0,1,2,…,Ni-1}(i=1,2,…,n),简记为{xi,k},k=0,1,2,…,Ni-1,i=1,2,…,n。令N=min{N1,N2,…,Nn},完全类似于前述,选取适当的正整数L(L≪N),对第i道信号执行下面三步:a)将{|Xi,m|},m=1,2,…,-1按从大到小的顺序排列,选取前L 项;b)将选出的前L 项根据其下标按从小到大的顺序重新排列,得到数组:(Xi,mi,1,Xi,mi,2,…,Xi,mi,L),其中,
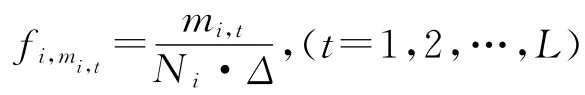
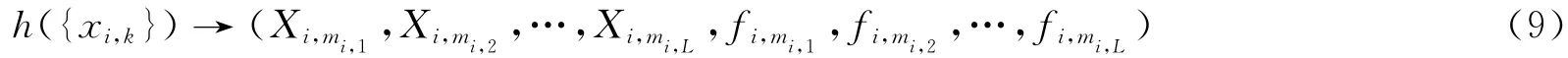
其中:
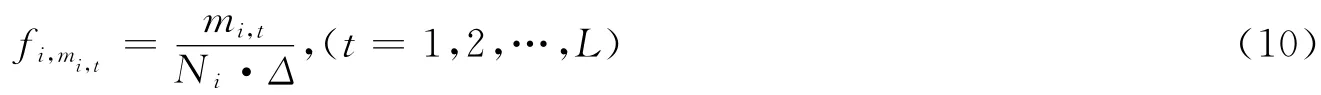
1.3 将V 空间上定义的距离作为U 空间上的广义距离

对于∀(Xi,mi,1,…,Xi,mi,L,fi,mi,1,…,fi,mi,L)∈V 和∀(Xj,mj,1,…,Xj,mj,L,fj,mj,1,…,fj,mj,L)∈V,定义实函数:
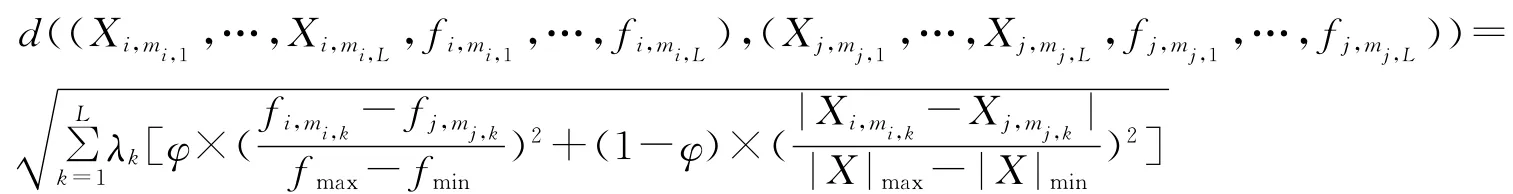
简记成:
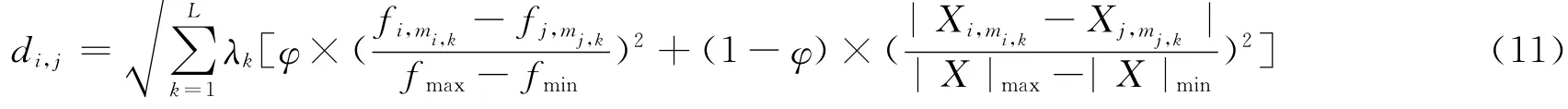
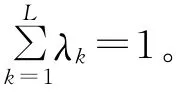
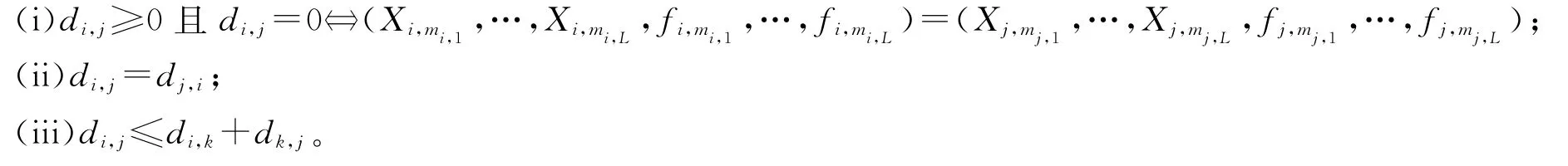
因而称di,j为空间V 上两点(Xi,mi,1,…,Xi,mi,L,fi,mi,1,…,fi,mi,L)与(Xj,mj,1,…,Xj,mj,L,fj,mj,1,…,fj,mj,L)之间的距离。由映射式(7)或式(9)知di,j也可以看成U 空间上的函数,即di,j=d({xi,k},{xj,k})。其中第i道信号{xi,k}与第j 道 信 号{xj,k}分 别 是V 中 两 点(Xi,mi,1,…,Xi,mi,L,fi,mi,1,…,fi,mi,L)与(Xj,mj,1,…,Xj,mj,L,fj,mj,1,…,fj,mj,L)在U 中的原像。尽管di,j=d({xi,k},{xj,k})作为U 上的函 数仍然满足条件:(i)di,j≥0;(ii)di,j=dj,i;(iii)di,j≤di,k+dk,j。但是由di,j=0一般推不出第i道信号{xi,k}与第j道信号{xj,k}信号完全相同。所以,di,j并不能作为U 空间上两道信号{xi,k}与{xj,k}之间的距离。但当di,j=0时,由映射式(7)或式(9)意味着两道信号{xi,k}与{xj,k}将有完全相同的L 主频谱与L 主频率,因而两信号必近似相同。故将di,j作为U 空间上信号{xi,k}与{xj,k}之间的广义距离是合适的。
2 超长离散信号聚类法
前文在U 空间上定义了两道信号之间的广义距离,接下来便可根据传统定义类与类之间距离的方法,如①最短距离法;②最长距离法;③中间距离法;④重心法;⑤类平均法;⑥可变类平均法;⑦离差平方和法等方法[7]对U 空间里的点进行聚类。
3 超长离散信号聚类法在全球验潮站潮型分布中的应用
“海平面联合档案”(JASL)是夏威夷大学、美国国家海洋学数据中心(NOAC)与世界海洋学数据中心(WDC-A)共同协作的成果,收录了全球约596个验潮站的海面波动信号资料。在采样间隔为1h的数据文件中发现1996年收录了326个验潮站,为历年最多。而在这一年,有181个验潮站收录了全部24×366=8 784个数据。对这些验潮站采用1.1节方法,将181个长度为8 784的海面波动信号映射到32维空间(这里L=16),得到每个信号的主频谱和主频率,然后在式(11)中取λ1=λ2=…λ16=及φ=1,采用类间平均距离进行聚类,得到了全球181个验潮站潮型分布图(图1)。
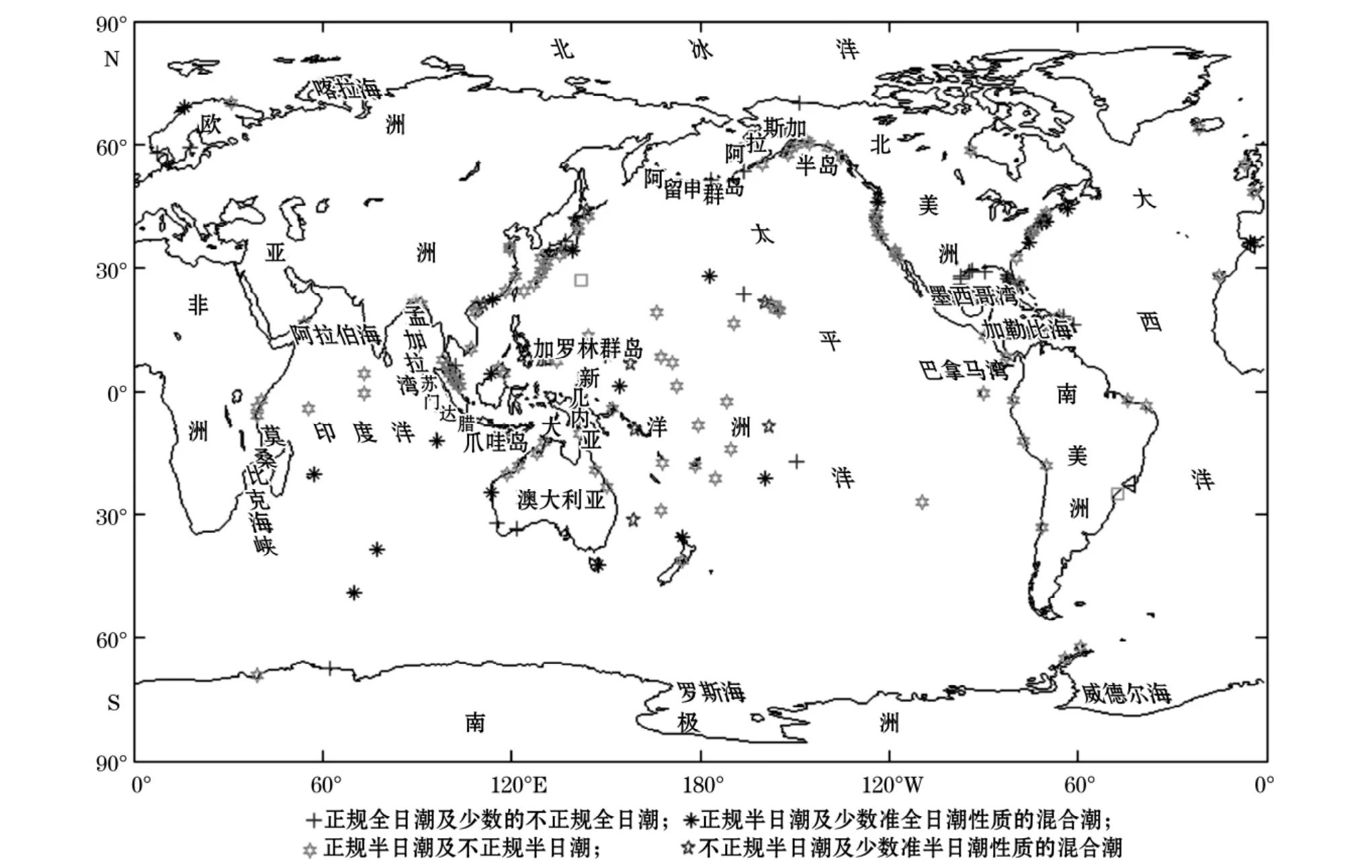
图1 1996年181个验潮站潮型分布图Fig.1 The distribution of tidal stencils based on the data sets from 181tide stations in 1996
如果将1996年有数据记录的所有326个验潮站皆考虑在内,则需要运用采用1.2节方法,将最小长度仅为970的326列海面波动信号映射到32维空间,得到它们的主频谱和主频率,在式(11)中同样取λ1=λ2=…λ16=及φ=1采用类间平均距离法进行聚类,便可得到全球326个验潮站潮型分布图(图2)。
根据方国洪等[10]相关资料得出的结论:在太平洋,正规全日潮及混合潮(不正规全日潮、不正规半日潮)较多,正规半日潮相对较少。在太平洋赤道与40°S之间的大部分地区,大洋中部的岛屿,巴拿马湾、阿拉斯加半岛沿岸,东海西侧,以及澳大利亚东岸等地都为正规半日潮;阿留申群岛东南、新几内亚(伊里安岛)东北岸、加罗林群岛等地为正规全日潮;西岸大部、北美沿岸及其余地区都是混合潮。大西洋的潮汐多属半日潮。西欧沿岸为正规半日潮,美洲东侧中部的加勒比海沿岸大部分为不正规半日潮;有些地方为不正规全日潮;墨西哥湾沿岸,除东部为不正规半日潮外,其余地区都是正规全日潮或不正规全日潮。印度洋的孟加拉湾、查戈斯群岛、莫桑比克、克罗泽群岛附近海区和澳大利亚西北近海,为正规半日潮;阿拉伯海、苏门答腊及爪哇岛近海都是不正规半日潮;澳大利亚西岸及南岸,属不正规全日潮,西南近海是正规全日潮。北冰洋的潮汐主要是由大西洋的潮波传入而引起的。除泰米尔半岛顶端及喀拉海东部沿岸为不正规半日潮外,其余沿岸地区均为正规半日潮。南大洋的潮波自东向西围绕南极大陆传播,以全日潮型为主,间有混合潮。罗斯海为全日潮,威德尔海为半日潮和全日潮。将这些结论与图1、图2给出的聚类结果比对发现两者吻合得很好。由此可见超长离散信号聚类方法的有效性。
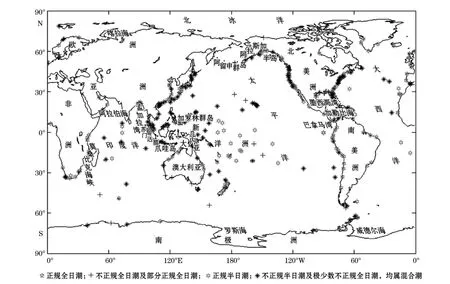
图2 1996年326个验潮站潮型分布图Fig.2 The distribution of tidal stencils based on the data sets from 326tide stations in 1996
4 结 论
本文借助有限离散信号的Fourier变换,通过将超长离散信号空间映射到低维空间,并由低维空间上的距离诱导出超长离散信号空间上的广义距离,实现了对超长离散信号的聚类。利用“广义距离”聚类虽然不如用“距离”更为精准。但是,采用广义距离将使计算量大大减少。就文中所提潮型聚类问题,若用传统的聚类方法需要计算8 784维空间任意两点之间的距离,而用本文所述方法只需计算32维空间里的距离。若仅考虑计算两点之间的距离一次,就能减少8 784-32=8 752次减法运算和8 752次乘方运算以及8 752次加法运算。像文中考虑326个验潮站潮型聚类问题,共需计算326×325×2=52 975次两点之间的距离,由此可见,利用新方法所减少的计算量是十分可观的。当两个超长离散信号的广义距离为0时,虽然得不出两个超长离散信号完全一致,但也可推知两者的主频谱和主频率是完全相同的,这对于许多超长离散信号的聚类问题来说足可得出较为满意的聚类结果。
:
[1] GONZALEZ T.Clustering to minimize and maximum intercluster distance[J].Theoretical Computer Science,1985,38(2-3):293-306.
[2] PAL N R,BEZDEK J C.On cluster validity for the fuzzy c-means model[J].IEEE Transactions on Fuzzy Systems,1995,3(3):370-379.
[3] DOUGLAS S,MICHAEL J B.Initializing k-means batch clustering:a critical evaluation of several techniques[J].Journal of Classification,2007,24(1):99-121.
[4] WU Z,LEATHY R.An optimal graph theoretic to data clustering:theory and its application to image segmentation[J].IEEE Transactions on Pattern Anal.Machine Intelligence,1993,15(11):1101-1113.
[5] HUANG Z X.Extensions to the k-means algorithm for clustering large data sets with categorical values[J].Data Mining and Knowledge Discovery,1998,2(9):283-304.
[6] CHAVENT M.A monothetic clustering method[J].Pattern Recognition Letters,1998,19(11):989-996.
[7] GUY A,NOAM G,NATHAN I.Cluster analysis and classification of heart sounds[J].Biomedical Signal Processing and Control,2009,(4):26-36.
[8] AVIV M,YOSSI Y.Cluster analysis of resting-state fMRI time series[J].NeuroImage,2009,45(4):1117-1125.
[9] SONG X Q,ZHANG P P,TANG G L,et al.The influence on fairwang trough capacity because of the number of regular semidiurnal tide and the average tidal range[J].China Water Transport,2011,11(7):70-72.宋向群,张培培,唐国磊,等.正规半日潮的潮型数及平均潮差对港口航道通过能力的影响[J].中国水运,2011,11(7):70-72.
[10] FANG G H,ZHENG W Z,CHEN Z Y,et al.Analysis and prediction of tides and tidal currents[M].Beijing:China Ocean Press,1986.方国洪,郑文振,陈宗镛,等.潮汐和潮流的分析和预报[M]北京:海洋出版社,1986.
[11] ZHANG Y T.Multivariate statistical analysis[M].Beinig:China Statistics Press,2002.张尧庭.多元统计分析选讲[M].北京:中国统计出版社,2002.
