带p-Laplace算子的分数阶微分方程耦合系统边值问题解的存在性

程玲玲 ，刘文斌，叶晴晴

(1.中国矿业大学理学院，中国 徐州 221008；2.南京理工大学理学院，中国 南京 210094)

分数阶微分方程有很强的应用背景，无论在物理学、生物学、化学、信号学等科学和工程领域都有非常重要的应用．许多学者都投身于分数阶微分方程的研究，其中包括对分数阶微分方程(系统)的研究见文献[1～8]，耦合系统就是其中一类．耦合关系是指两个具有相近相通，又相差相异的系统，不仅有静态的相似性，也有动态的互动性．它们之间的相互作用，相互影响，是研究的主要方面．苏新卫在文献[1～2]中分别讨论了分数阶微分方程耦合系统的边值问题解的存在性．

文献[1]中研究了

文献[2]中研究了

的解的存在性，其中1<α,β≤2,u,v>0,α-v≥1,β-u≥1，f,g:[0,1]×R×R→R是连续的，D表示Riemann-Liouville型分数阶导数．

本文在文献[1～2]的基础上主要研究了下面带有p-Laplace算子分数阶微分方程耦合系统边值问题

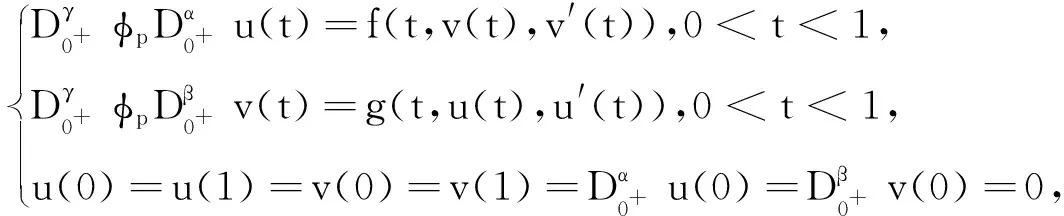
(1)

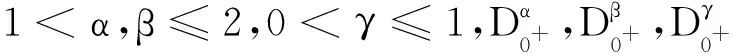
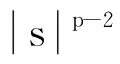
1 预备知识

定义1[1]连续函数u(t):R+→R的α次Riemann-Liouville型积分为

其中α>0．

定义2[1]连续函数u(t):R+→R的α次Caputo型微分为

其中α>0，n=[α]+1．

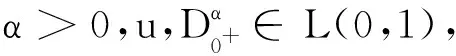
引理2[10]设U为Banach空间X的一个有界闭凸子集，如果T：U→U为全连续算子，那么T在U内至少有一个不动点．

引理3[11]φp(s)有如下性质

也可表示成φp(s+t)≤2p-1(φp(s)+φp(t)),p>1,s,t>0．

2 主要结果

在给出主要定理之前先给出两个引理．

引理4设g(t)∈C[0,1],1<α≤2，则

(2)

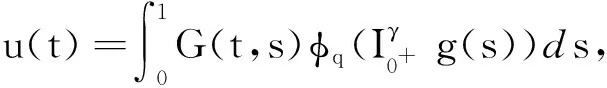
(3)

为(2)的格林函数．

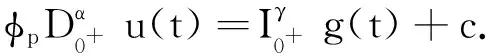
(4)

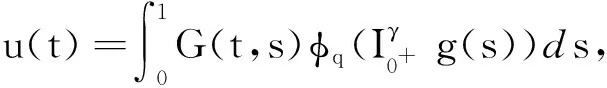
引理5微分方程系统(1)等价于积分方程系统

证由引理4可以直接得到，证明略．

设(u,v)∈X×X，根据引理5定义算子T如下

(T1v(t),T2u(t)).

易知，若算子T存在不动点则边值问题(1)有解．

下面给出本文主要定理．

定理1设f,g:[0,1]×R→R为连续函数，满足以下条件

(H1) 存在非负函数ai(t),bi(t)∈C[0,1],i=1,2,3和非负连续函数hj(x),kj(x):R→R,j=1,2，使得|f(t,x)|≤a1(t)+a2(t)h1(x)+a3(t)h2(x),|g(t,x)|≤b1(t)+b2(t)k1(x)+b3(t)k2(x)成立；

下面证明T:U→U，设(u,v)∈U，应用条件(H1)及引理3得

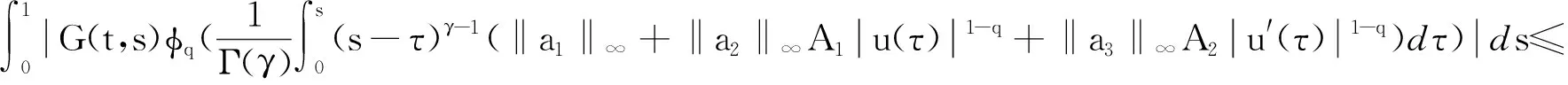
同理可推得|T2v(t)|

下证T是等度连续的，对任意的(u,v)∈U，注意到f,g有界，设

同理可推得|T2u(t1)-T2u(t2)|<ε.所以TU是等度连续的，同时又是一致有界的，由Arzela-Ascoli定理可得T是全连续算子，应用引理2知T存在不动点，进而问题(1)存在解．

参考文献：

[1] 苏新卫．分数阶微分方程耦合系统边值问题解的存在性[J]．工程数学学报, 2009，26(1)：133-137．

[2] SU X W．Boundary value problem for a coupled system of nonlinear fractional differential[J]．Appl Math Lett， 2009,22(1)：64-69．

[3] ZHOU W X, PENG J G．Existence of solutions to boundary value problem for fractional differential equations[J]．Chin J Engin Math, 2011，22(6):727-735．

[4] BASHIR A, SOTIRISK N, AHMED A．New existence results for nonlinear fractional differential equations with three-point Integral boundary conditions [J]．Adv Differential Equ, 2011,10(11)：1687-1847．

[5] ZHOU Y, JIAO F, LI J. Existence and uniqueness for p-type fractional equations[J]．Nonlinear Anal-Theorem, 2009，71(7-8)：2724-2733．

[6] CABALLERO J, HARJANI J, SADARANGANI K. Existence and uniqueness of positive and nondecreasing solution for a class of singular fractional boundary value problems[J]．Bound Value Prob, 2009，10(10)：1687-2770．

[7] LI C F, LUO X N, ZHOU Y. Existence of positive solutions of boundary value problem for nonlinear fractional differential equations[J]．Comput Math Appl, 2010，59(2)：1363-1375．

[8] CABALLERO J, HARJANI J, SADARANGANI K. On existence and uniqueness of positive solutions to a class of fractional boundary value problems[J]．Bound Value Prob, 2011，101(10):687-2770．

[9] KILBAS A A, SRIVATAVA H M, TRUJILLO J J. Theory and application of fractional differential equations [M]．Elsevier： Amsterdam， 2006．

[10] CHENG Y, GAO G Z. Existence of fractional differential equations[J]．J Math Appl, 2005，310(1)：26-29．

[11] 葛渭高．非线性微分方程边值问题[M]．北京：科学出版社, 2009．