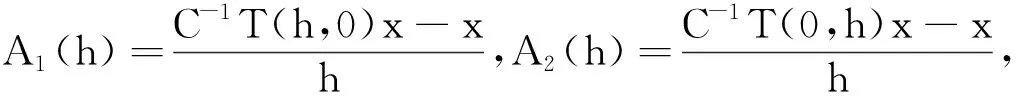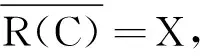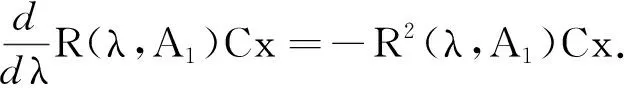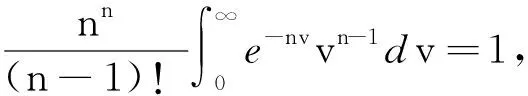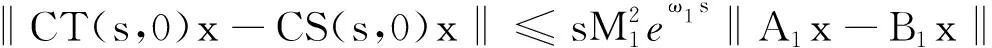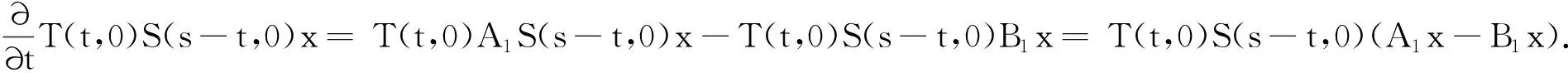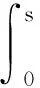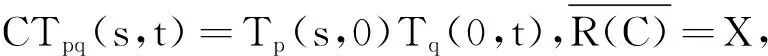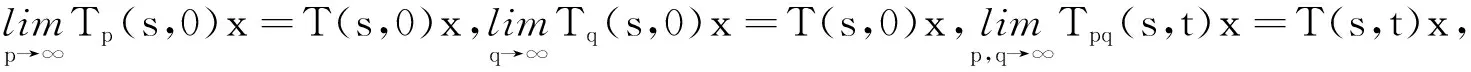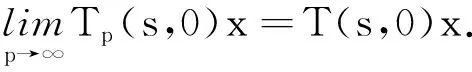指数有界双参数C半群的逼近
2013-11-21宋晓秋
岳 田,宋晓秋
(中国矿业大学理学院,中国 徐州 221116)
自Hille[1]首先提出算子半群理论以来,其理论得到不断丰富和发展.尤其是近年来,受一些具体问题如具有非稠定算子的抽象Cauchy 问题的激发,已有10余种算子半群或算子族相继被国内外众多学者广泛关注,并取得了一系列成果[2-11].其中对于算子半群逼近问题的讨论,有力地推动了大量实际问题的研究,如在平面上的Markov扩散过程,人类学中的人口发展问题,物理学中的中子迁移系统渐近状态的研究等方面显示出较好的实际意义.
众所周知,经典的单参数算子半群理论已日益完善,并得到了广泛应用.与其相比,双参数半群理论研究进展缓慢,还有许多不完善之处,近些年来,已有一些学者对其进行了初步研究.如文献[5]给出了双参数强连续算子半群的定义及其与生成元之间关系的若干性质;文献[6]给出了双参数强连续算子半群的预解式的系列性质;文献[7]介绍了双参数强连续算子半群的收敛性问题;文献[8]对双参数C半群的基本性质及Cauchy问题进行了讨论.本文在上述文献的基础上,结合单参数C半群的相关理论,讨论了指数有界的双参数C半群的逼近定理.
1 定义及相关引理
在本文中,设(X,‖·‖)为Banach空间,L(X)表示所有从X到自身的线性算子的全体,记B(X)为X上一切有界线性算子构成的Banach代数.设A为X中的线性算子,D(A) ,R(A) ,R(λ,A) 分别表示定义域,值域及预解式.算子C∈B(X)为单射,记ρC(A)为A的C预解集,其中ρC(A)={λ:λ-A为单射且R(C)⊂R(λ-A)}. (λ-A)-1C为A的C预解式,R+2表示二维非负实数空间.
定义1[8]若双参数算子族{T(s,t)}s,t≥0⊂B(X)满足:
1)T(0,0)=C;
2)T(s+s′,t+t′)C=T(s,t)T(s′,t′),∀s,s′,t,t′≥0;
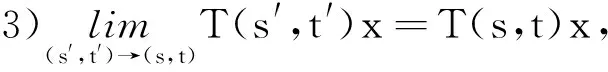
则称其为X上的双参数C半群.
进一步地,若存在M≥‖C‖,ω∈R,使得对∀s,t≥0,有‖T(s,t)‖≤Meω(s+t),则称双参数C半群{T(s,t)}s,t≥0为指数有界的双参数C半群.
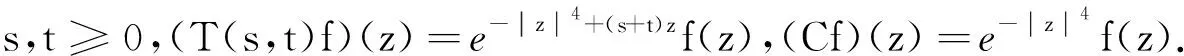
对任意的s,t≥0 ,由定义1中性质2)可得
T(s,t)C=T(s,0)T(0,t)=T(0,t)T(s,0),T(s,0)C=CT(s,0),T(0,t)C=CT(0,t),
这意味着{T(s,0)}s≥0和{T(0,t)}t≥0是2个可交换单参数C半群.对此,不妨设A1和A2分别是单参数C半群{T(s,0)}s≥0和{T(0,t)}t≥0的无穷小生成元,那么
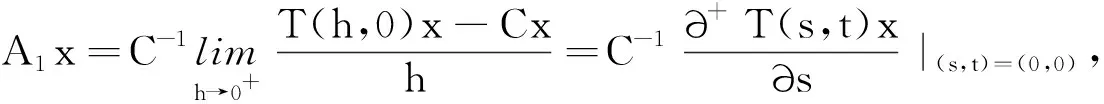
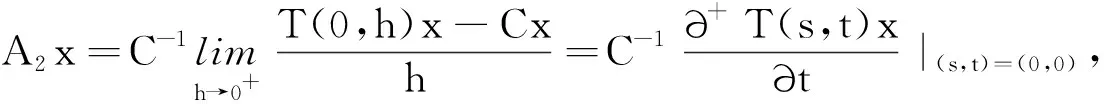
这里,
定义2双参数C半群{T(s,t)}s,t≥0的无穷小生成元A定义如下:
引理1双参数C半群{T(s,t)}s,t≥0的无穷小生成元是线性变换L:R+2→L(X) ,其定义为L(a,b)x=(A1,A2)(a,b)Tx=aA1x+bA2x,∀x∈X,(a,b)∈R+2.这里,算子A1和A2分别是单参数C半群{T(s,0)}s≥0和{T(0,t)}t≥0的无穷小生成元.
证类似文献[5]中定理2.3.
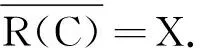
证设‖T(t)‖≤Meωt,其中ω≥0 ,A是T(t)的无穷小生成元.因为对每一h>0,A(h)有界,故etA(h)是可定义的.而且由于A(h)与T(t)可交换, etA(h)和T(t)亦是如此.又
因此对于0 所以对于0 tM2exp{t(eω+ω-1)}‖Ax-A(h)x‖. 证因为对每一h>0 ,A1(h)和A2(h)均是有界的,故esA1(h)和etA2(h)是有意义的,且二者是可交换的.则对∀x∈X有 ‖C2esA1(h)etA2(h)x-CT(s,t)x‖=‖C2esA1(h)etA2(h)x-T(s,0)T(0,t)x‖≤ ‖C2esA1(h)etA2(h)x-T(s,0)CetA2(h)x‖+‖T(s,0)CetA2(h)x-T(s,0)T(0,t)x‖≤ ‖CetA2(h)‖‖CesA1(h)x-T(s,0)x‖+‖T(s,0)‖‖CetA2(h)x-T(0,t)x‖. 又因为A1(h)和A2(h)是有界可交换的,故esA1(h)etA2(h)=esA1(h)+tA2(h),∀h>0.进而有 且上述极限在s,t的任何有限区间上的收敛是一致的. 即 定理3设(A1,A2),(B1,B2)分别是双参数C半群{T(s,t)}s,t≥0和{S(s,t)}s,t≥0的无穷小生成元,若 1)对于s≥0,有‖T(s,0)‖≤M1eω1s,‖S(s,0)‖≤M1eω1s; 2)对于s≥0,x∈X,有T(s,0)S(s,0)=S(s,0)T(s,0). 证当x∈D(A1)∩D(B1)时,此时可将双参数C半群T(s,0),S(s,0)视为单参数C半群.则如下等式成立: 上式两端从0到s积分可得 则有 1)对于s,t≥0,有‖T(s,0)‖≤M1eω1t,‖Tp(s,0)‖≤M1eω1t; 2)对于s,t≥0,有‖T(0,t)‖≤M2eω2t,‖Tq(0,t)‖≤M2eω2t; 3)D(A1)⊂D(Ap),D(A2)⊂D(Aq)(p,q∈N); 4)对于s,t≥0,有T(s,0)Tp(s,0)=Tp(s,0)T(s,0),T(0,t)Tq(0,t)=Tq(0,t)T(0,t); 证当x∈D(A1)∩D(Ap),且0≤s≤T时,可将双参数C半群Tp(s,0),T(s,0)视为单参数C半群.从而由定理3可得 参考文献: [1] HILLE E, PHILLIPS R S. Functional analysis and semigroups[M]. New York: Am Math Soc Colloq Pub,1957. [2] PAZY A. Semigroups of linear operators and applications to partial differential equations[M]. New York: Springer-verlag, 1983. [3] PFEIFER D. Approximation-theoretic aspects of probabilistic representations for operator semigroups[J].J Approx Theory, 1985,43(3):271-296. [4] ADRENT W. Vector-valued Laplace transforms and Cauchy problems[J]. Isr J Math, 1987,59(3):327-352. [5] SHARIF A S, KHALIL R. On the generator of two parameter semigroups[J]. Appl Math Comput, 2004,156(2):403-414. [6] 蔡 亮,宋晓秋,禹晓红.双参数C0半群的指数公式与预解式[J]. 徐州师范大学报, 2010,28(4): 43-45. [7] 禹晓红,宋晓秋,李玉霞,等.双参数C0半群的收敛性问题[J]. 贵州大学学报, 2011,28(3):4-6. [8] JANFADA M. On two-parameter regularized semigroups and the cauchy problem[J]. Abstract Appl Anal, 2009,2009:1-15. [9] LI Y C, SHAW H Y. N-times integrated C-semigroups and the abstract cauchy problem[J]. Taiwan J Math, 1997,1(1):75-102. [10] 陈文忠.C-无穷小生成元的表示式[J]. 厦门大学学报, 1993,32(2):135-140. [11] 徐景实,周放军. Toeplitz型算子在变指数空间的有界性[J]. 湖南师范大学自然科学学报, 2011,34(1):1-4.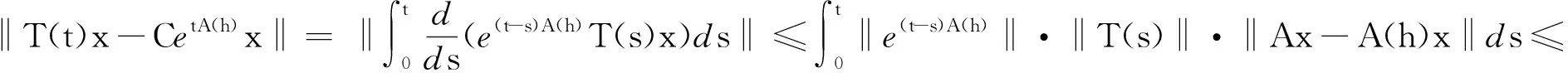
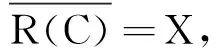

2 主要结论