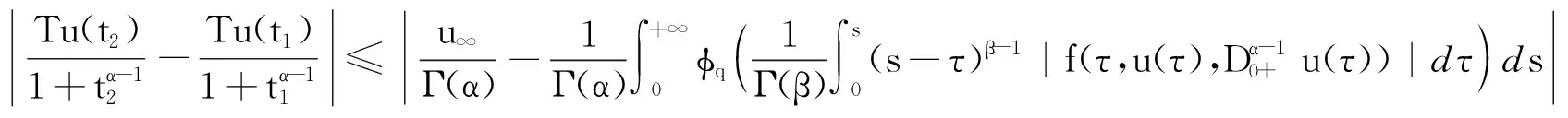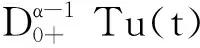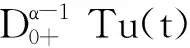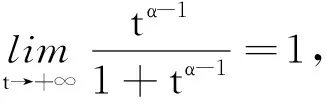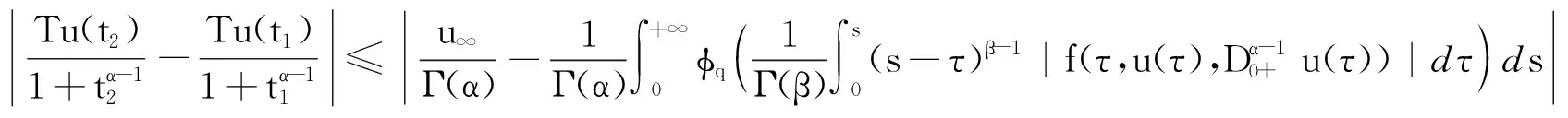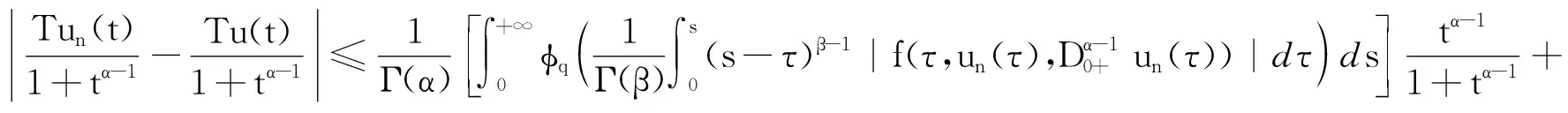带p-Laplacian算子的分数阶微分方程边值问题在无穷区间中解的存在性

胡 宏 ，徐 娜

(1.徐州工程学院数理学院，中国 徐州 221116；2.中国矿业大学理学院，中国 徐州 221116)

近年来，分数阶微分方程在国内外引起了极大的研究兴趣，特别是边值问题解的存在性[1-4]．据作者所知，目前很少有学者研究带p-Laplacian算子的分数阶微分方程边值问题解的存在性[5-6]，尤其是无穷区间中解的存在性研究甚少[7]．

无穷区间上的边值问题在物理学、自然科学等领域中有很多实际应用，如不稳定的气体通过半无穷带气孔媒介问题，孤立中子的电势问题等[8-10]．因此，对它的研究具有重要的意义．

受以上文献的启发，本文主要利用Schauder不动点定理研究如下一类带p-Laplacian算子的分数阶微分方程边值问题在无穷区间中解的存在性：

(1)

1 预备知识

定义1函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶积分为

其中α>0,Γ(·)是Gamma函数.

定义2函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶导数为

其中α>0,Γ(·)是Gamma函数，n=[α]+1.

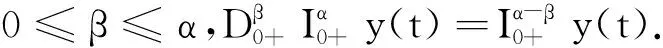
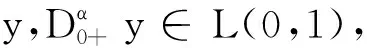
引理3[11](X,‖·‖X)和(Y，‖·‖Y)是Banach空间.

本文主要是在空间Y中研究解的存在性，但Arzela-Ascoli定理在Y中紧性不再适用，因此，我们给出如下引理来证明相对紧.

引理4[11]令Z是Y的有界子集，若Z是Y中的相对紧集需要满足如下条件：

(ii)对任意的ε>0,存在常数T=T(ε)>0,满足

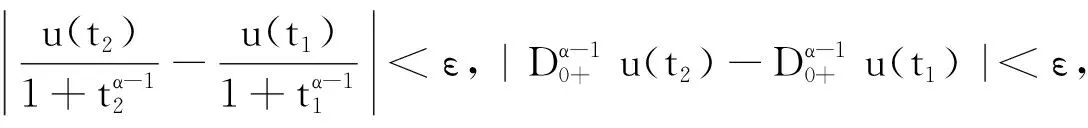
引理5[12]设K是Banach空间X的1个有界凸闭集，而T是K到其自身内的任一全连续映象，则T在K内至少有一个不动点.

2 主要结果

为了得到本文主要结果，假设：

引理6假设(H)成立，则对任意的t∈J,边值问题(1)等价于如下积分方程：

(2)

证首先，由(H)得

c‖u‖Y<+∞.

(3)

因此，积分方程(2)是存在的.

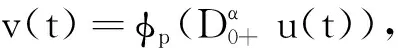
由引理2得

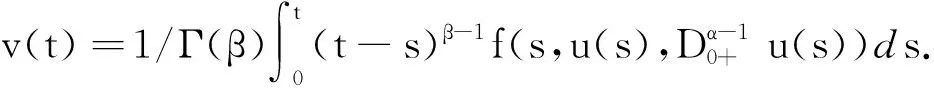
再次利用引理2得

因为u(0)=0,所以c2=0.由引理1，进一步得

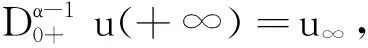
从而积分方程(2)成立.

另一方面，若积分方程(2)成立，那么由引理1可以得到如下方程：

定理1假设f∈C(J×R2,R)并且条件(H)成立，那么边值问题(1)在Y中至少有一个解.

证首先，对任意的t∈J,定义算子T：

(4)

由引理6，知边值问题(1)的解可以转化为求算子T的不动点.由(4)及引理1，得

(5)

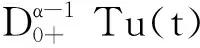
令M≥|u∞|/(Γ(α)-2c),U={u(t)∈Y|‖u‖Y≤M}.下面将证T：U|→U.

对任意的1<α≤2,t,s∈J,并且t>s,显然有(t-s)α-1/(1+tα-1)≤tα-1/(1+tα-1)≤1.对任意的t∈J,u(t)∈U,1<α≤2,由(4)和(5)分别得

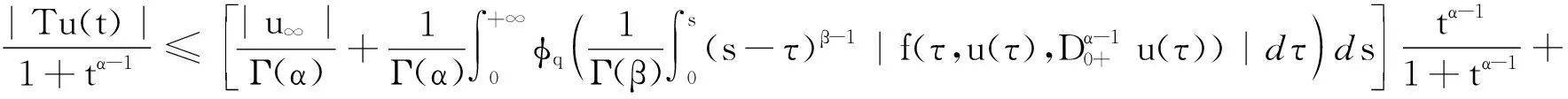
(6)

(7)

由(3)，(6)，(7)及M≥|u∞|/(Γ(α)-2c),可以得

因此‖Tu(t)‖Y≤M,即T：U|→U.

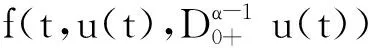
对任意的u(t)∈D,t1,t2∈I满足t1

那么，对任意的ε>0,存在常数L>0满足

(8)

(9)

(10)

取T=max{T1,T2},对任意的t1,t2>T,u(t)∈D,由(8)～(10)得

类似地，可得

因此，由引理4，我们可以得TU是相对紧的.

最后，我们证明T：U|→U是连续算子.对任意的t∈J,un,u∈U(n=1,2,…),并且满足‖un-u‖Y→0(n→+∞),那么

结合(3)，进一步可得

类似地，我们得

2c‖un‖Y+2c‖u‖Y≤4c‖u‖Y≤2Γ(α)M≤2M.

因此，由Lebesgue控制收敛定理可得T：U|→U是连续的.

综上，由引理5得，算子T在U中至少有一个不动点，从而边值问题(1)在U中至少有一个解.

参考文献：

[1] BAI Z B, LÜ H. Positive solutions for boundary value problem of nonlinear fractional differential equation [J].J Math Anal Appl, 2005,311(2):495-505.

[2] XU X, JIANG D, YUAN C. Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation [J]. Nonlinear Anal-Theor, 2009,71(10):4676-4688.

[3] CHANG Y, NIETO J. Some new existence results for fractional differential inclusions with boundary conditions[J]. Math Comput Model, 2009,49(3):605-609.

[4] JIANG W H. The existence of solutions to boundary value problems of fractional differential equations at resonance [J]. Nonlinear Anal-Theor, 2011,74(5):1987-1994.

[5] CHAI G Q. Positive solutions for boundary value problem of fractional differential equation withp-Laplacian operator [J]. Bound Value Probl, 2012,2012(1):1-18.

[6] CHEN T Y, LIU W B, HU Z G. A boundary value problem for fractional differential equation withp-Laplacian operator at resonance [J]. Nonlinear Anal Theor, 2012,75(6):3210-3217.

[7] LIANG S H, SHI S Y. Existence of multiple positive solutions form-point fractional boundary value problems withp-Laplacian operator on innite interval [J]. J Appl Math Comput, 2012,38(1):687-707.

[8] NACHMAN A, CALLEGARI A. A nonlinear singular boundary value problem in the theory of pseudoplastic fluids [J]. Siam J Appl Math, 1980,38(2):275-281.

[9] AGARWAL R, O’REGAN D, WONG P. Positive solutions of differential, difference and integral equations (1st edition) [M]. Massachusetts: Kluwer Academic, 1998.

[10] 肖 莉.一类p-Laplacian系统同缩轨道的存在性[J].湖南师范大学自然科学学报, 2010,33(1):7-12.

[11] SU X W, ZHANG S Q. Unbounded solutions to a boundary value problem of fractional order on the half-line[J]. Comput Math Appl, 2012,61(4):1079-1087.

[12] 尤秉礼.常微分方程补充教程[M].北京：人民教育出版社, 1981.