基于卡尔曼滤波技术的医疗检测信号最优估计算法研究

黄 静，欧凤霞

(安徽中医学院 医药信息工程学院，安徽 合肥 230031)

医疗领域的信号处理主要是利用多种医疗设备检测信号进行病理评估，如脑电图、心电图的检测信号.由传感器采集人体的生物电信号，经过信息融合后进行评估，这样比单由专家通过目测标注更能提高检测效果.本研究所介绍的算法以标准的卡尔曼滤波为基础，通过递归方式由离散小波变换滤波层实现对检测信号的最优估计.

1 信号的分解和估计

1.1 离散小波变换

在分辨尺度i+1上，对给定的标量信号序列x(i+1，n)∈l2(Z)(n∈Z)，通过脉冲响应为h(n)的低通滤波器可以获得在低分辨率上的信号

(1)

这是一个从向量空间l2(Z)到它自身的变换，下标L表示x(i，n)在粗尺度信号空间Li-1上的投影.信号x(i+1，n)在低通滤波器中丢失的“细节信号”可以由x(i+1，n)通过一个脉冲响应为g(n)的高通滤波器得到,

(2)

原信号x(i+1，n)可以由两个滤波器及平滑信号xL(i，n)和细节信号xH(i，n)进行恢复.为了完整恢复原信号，滤波脉冲响应构成正交集.因此，式(1)和式(2)是在正交基础上对原信号的分解.原信号重构是一系列正交投影构成：

(3)

h(n)和g(n)是有限持续脉冲响应滤波器，低通滤波h(n)是一个正交镜像滤波器脉冲响应，且h(n)和g(n)形成一个共轭镜像滤波对：

g(n)=(-1)nh(L-1-n)，

(4)

其中，L是滤波器的长度(需是偶数)[1].

式(4)意味着低通滤波器h(n)一旦确定，与之共轭的高通滤波器g(n)也被确定.

对于有限长度信号序列，常以算子形式来描述小波变换.在分辨尺度计1上，长度为M的信号序列为

(5)

由式(1)，(2)和(3)的向量形式得到算子形式如下：

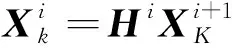
(6)

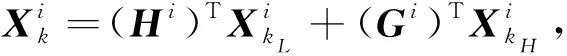
(7)

其中,Hi和Gi是相应的尺度算子与小波算子，且满足

(Hi)THi+(Gi)TGi=I，

(8)

(9)

(10)

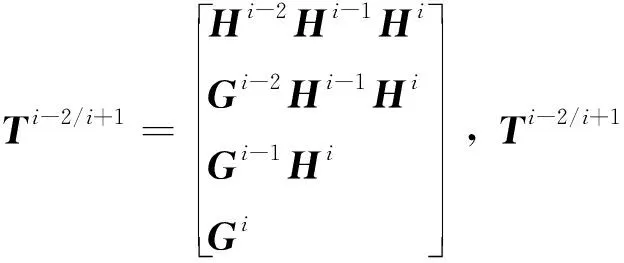
1.2 信号的分解和估计

在最高分辨尺度N上，信号序列x(N,k)的状态方程和观测方程如下：

(11)

z(N，k+1)=C(N，k)x(N，k)+v(N，k)，

(12)

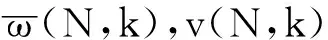
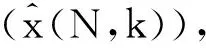
为了描述简单起见，仅讨论信号两层的同时分解和估计，即从尺度N到N-1和N-2，其他尺度的分解和估计依次类推.在K时刻，对长度为M=22=4的数据块，信号序列为

(13)

假设时间不变，尺度N是递减的，则信号以M为单位进行传输.由式(12)和式(13)信号推导如下：

因为

(14)

得

(15)

(16)

(17)

将式(14)～(17)相加，经过变形，得到

(18)

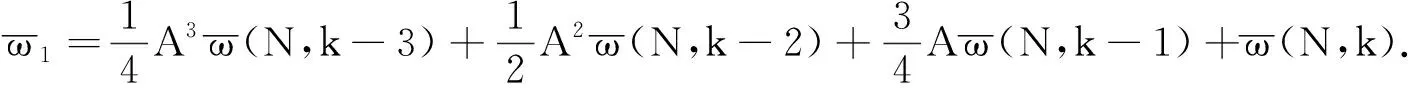
考虑所有的递推过程，给出数据块形式的动态方程及测量方程.

(1)动态方程

(19)

(2)测量方程

(20)

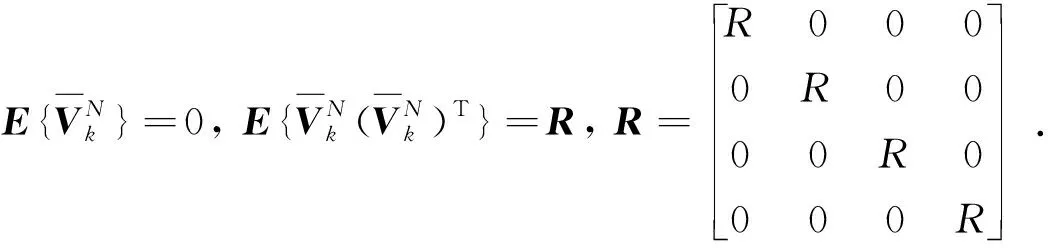
由上述的推导过程，可得两层的分解如下式：

(21)

(22)

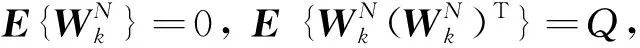
式(22)描述了分解量的动态系统模型，与之相联系的测量模型可由式(21)代入式(20)得到

(23)

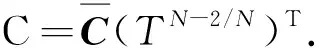
至此，分解量的系统模型和测量模型便得到，通过测量方程可以对分解量进行估计.将卡尔曼滤波算法代入式(22)和式(23),可得到分解量的最优估计[4].

2 仿真实验

以一维的函数为例，其状态方程和观测方程如下：

x(N，k+1)=x(N，k)+w(N，k),

(24)

z(N，k+1)=x(N，k)+v(N，k),

(25)

其中,E{w(N，k)}=0，E{w2(N，k)}=Q；E{v(N，k)}=0，E{v2(N，k)}=R.

图1 不同算法的信号估计Fig.1 Signal estimations of the different algorithms

通过对220次计算机仿真结果进行统计对比，将两种方法的误差均方根列于表1.由表1可以看出将卡尔曼滤波与小波相结合的算法性能优于仅仅使用卡尔曼滤波算法.

表1 两种算法估计误差方差的统计表Tab.1 Estimation error variance of two algorithms

3 结论

本算法在保留卡尔曼滤波对信号最优估计的基础上，将离散小波变换与标准卡尔曼滤波算法相结合，实现了对医疗设备检测信号的同步分解和估计.

参考文献：

[1] Wong P W.Wavelet decomposition of harmonizable random process[J].IEEE Trans Inform Theory,1993(39):7-18.

[2] 杨福生.小波变换工程分析的应用[M].北京:科学出版社,2006.

[3] Mallat S G. A theory for multiresolution singal decomposition: the wavelet representation[J]. IEEE Trans on Pattern Anal Machine Intell, 1989,11(7):674-693.

[4] 文成林，周东华.多尺度估计理论及其应用[M].北京:清华大学出版社，2002.