地震导致渗漏的供水管网水力模拟
2013-11-20龙天渝郭劲松李灵芝
杜 坤,龙天渝,郭劲松,安 强,李灵芝
(1.重庆大学 三峡库区生态环境教育部重点实验室,重庆 400045;2.西南交通大学峨眉校区 机械工程系,四川 峨眉 614202)
历次震害统计表明,各种埋地管线在地震中会遭受不同程度的破坏。汶川地震中都江堰市供水管网约有60%受损,管网渗漏点达2000余处,供水压力仅为震前供水压力的一半[1]。供水管网作为重要的生命线工程系统之一,震损不仅对人们的生产与生活产生影响,而且使生命及财产等面临火灾等的潜在危害[2]。因此,开展地震导致渗漏的供水管网的水力特性研究具有重要意义。
针对渗漏供水管网的水力模型与分析计算,Lin[3]在假定渗漏点压力等于零(大气压)且渗漏量为常数的条件下对渗漏管网进行了水力分析。Lin的假设较适用于爆管状态下的供水管网,对于中等渗漏的供水管网,渗漏点压力不为零,且渗漏量与压力相关。为此,陈玲俐等[4]提出“点式渗漏模型”,在管网节点用水量不变的假设下进行了渗漏管网的水力计算。然而,管网节点用水量不变的假设仅适用于渗漏量很小的情况,当渗漏量达到一定程度时,供水管网将处于低压工作状态,用水节点的实际配水量将减少,若仍假定所有节点用水量不变,部分节点的计算水压可能为负值,这将导致负压出流的不合理现象。因此,对低压供水管网的水力计算,需考虑节点流量随水压的动态变化[5]。低压用水点的流量随水压的变化关系通常不能用单一函数来表示[6-9],这大大增加了管网水力方程求解的计算量,且采用传统的迭代方法进行水力计算时,迭代的收敛与否将取决于初始值的选取,并且难以直接应用现有的商业软件求解。为解决该问题,Pathirana[10]利用EPANET软件中喷嘴出流模拟低压用水点时,通过修改传统的迭代步骤与计算引擎,实现了低压供水管网在EPANET软件中的水力计算。但当管网中存在渗漏点时,由于渗漏点与低压用水点的流量都随水压动态变化,为实现低压用水点的水力模拟与自动识别,修改后的计算引擎屏蔽了渗漏点的模拟功能,因此不适用于管网中存在渗漏点的水力计算。对于地震导致渗漏的供水管网的水力模型及水力分析,基本上都是采用常用的渗漏水力模型,而渗漏模型均未考虑地震烈度的影响。为预测地震导致渗漏的供水管网的水力状态,首先应构建相应的水力模型,为此,笔者引入日本水道协会提出的震害计算式改进地震导致的供水管网渗漏的计算方法,构建了地震诱发渗漏的供水管网的水力模型。
管网的水力模型是非线性代数方程组,需要通过迭代求解。为避免计算过程中迭代的发散和提高迭代的收敛速度,实现低压用水点与渗漏点在迭代中的同步计算,且迭代的收敛与否不依赖初始值的选取,笔者对常用水力计算迭代方法进行改进,提出了“分步迭代”的水力计算法。该方法首先根据管网震损评估结果在管段中添加虚拟渗漏点,并假设所有用水节点为低压用水点,对管网进行首轮迭代;依据首轮迭代结果修正用水节点的出流类型;然后进行第2轮迭代,当管网中各用水节点出流状态满足约束条件时完成水力计算。
1 地震导致渗漏的供水管网水力模型
管网中的水流满足质量守恒与能量守恒,其基本方程为:
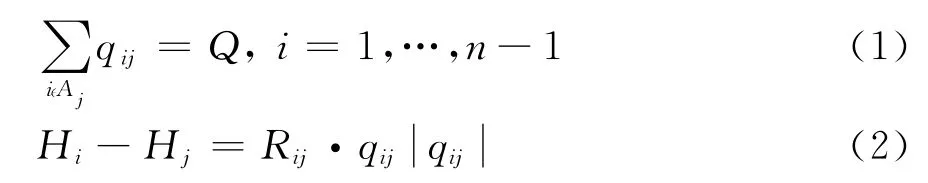
式中,qij为管段流量,n为管网节点数,Aj为与i节点直接相连的节点集合,Qi为节点流量,Rij为管段的水损系数,Hi和Hj分别为i、j节点的水压。当管网中存在渗漏时,需补充渗漏流量和压力的关系;当渗漏等引起供水管网处于低压状态时,导致部分节点流量变化,还需补充节点流量变化关系,这样才能使方程(1)和(2)封闭。
1.1 管段渗漏点的水力方程
假定地震诱发的管段渗漏为点式渗漏,根据已有研究[6],渗漏点的流量与水压的关系采用:

式中,QL为渗漏量,L/s;AL为管段渗漏面积,m2;HL为虚拟渗漏点水压,m。地震中管段渗漏量与管段渗漏面积相关,由于影响渗漏面积的因素复杂,假设管段的渗漏面积与管段在地震中的失效概率满足反弦函数关系[11]:
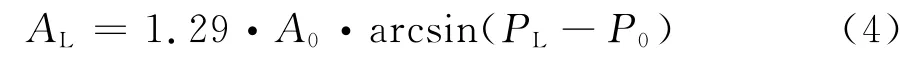
式中,A0为管段面积;A0=,DL为管段管径;PL为管段失效概率;P0为建议起始概率,此处P0=0.3,即当c≤0.3,AL=0。联立式(3)和式(4),得地震诱发的供水管段渗漏的渗漏方程为:
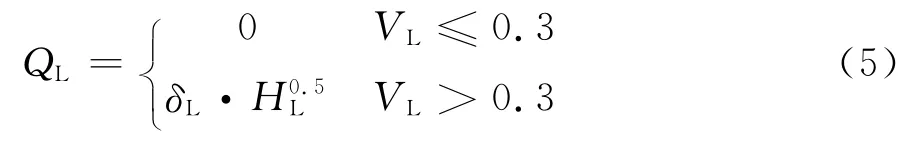
定义δL为地震时管段渗漏系数,δL=426··arcsin(PL-0.3)。要应用式(5)计算地震时管段的渗漏量,需确定管段在地震中的失效概率。地震导致管段的失效概率与管段的材质、管径、管长、接口形式、场地条件、地震动参数等因素有关[12-13]。由于采用理论方法计算失效概率十分困难,通常采用统计方法进行估算。通过分析发现,采用日本水道协会提出的统计计算式更适用于管段震损失效概率的估算[14]。研究表明,地震时管道的失效概率PL服从泊松分布:

式中:L为计算管段长度,m;λ为平均震害率(每km管道破坏次数),且λ=CP·Cd·Cg·Cy·R(v);CP为管材修正系数;Cd为管径修正系数;Cg为地形地质修正系数;Cy为土壤液化修正系数;R(v)为标准震害率,且R(v)=3.11×10-3×(v-15)1.3;v为地震峰值速度,cm/s,各参数取值参见文献[14]。
1.2 低压用水点的水力方程
由于地震引起供水管网漏损,导致用水点处于低压状态,低压用水点的流量随水压的变化关系通常不能用单一函数来表示而服从分段函数的关系,且难以用理论方法导出。为了实现低压用水点与漏损点在迭代过程中的同步计算,假定低压用水点的流量与压力满足如下分段函数[10]:

式中,Hi为i节点的供水压力;为保证正常用水量的最小水压为节点i在正常供水压力下的用水量;一般=10~20m(根据各节点的用水特征取值);S=。i
2 低压状态下供水管网水力计算
在采用传统的迭代法对式(1)、(2)求解时,由于低压用水点无法被预先识别,因此节点用水量Q可能为常数或为与压力H 相关的变量,若选取的迭代初始值(q或H )与实际中节点的出流状态不符,将导致计算结果的错误或迭代无法收敛。
为避免计算结果依赖于迭代初始值的选取,可将传统的迭代法修改为分步迭代。首先,在迭代的开始假设所有用水节点都处于低压工作状态,使迭代初始值的选取与节点的出流状态无关。然后,对管网进行第一轮迭代,若计算结果中节点i的水压Hi≥,表明该节点不处于低压工作状态,则在第2轮迭代的开始将该节点修正为正常出流类型。最后,对修正后管网进行第2轮迭代,根据管网处于稳态时的水力状态设置相应约束,当管网中所有节点的出流状态都满足约束条件时,则迭代结束并完成水力计算。
3 基于EPANET的地震时供水管网水力状态预测
EPANET是由美国环保局开发的管网水力分析软件,使用者可根据不同需要调用其计算引擎进行管网的水力计算。其提供了喷嘴出流的水力模型,喷嘴的流量与压力满足如下函数关系[15]。

式中:Q为喷嘴出流量,L/s;C为扩散系数;p为喷嘴工作压力,m;r为压强系数。在利用EPANET软件对管网进行水力计算时,可采用喷嘴出流模型模拟低压用水点与渗漏点,对渗漏节点CL=δL,对低压用水节点Ci=Si,压强系数r=0.5。地震产生渗漏时,当供水管网处于稳态时各节点出流状态应满足如下条件:
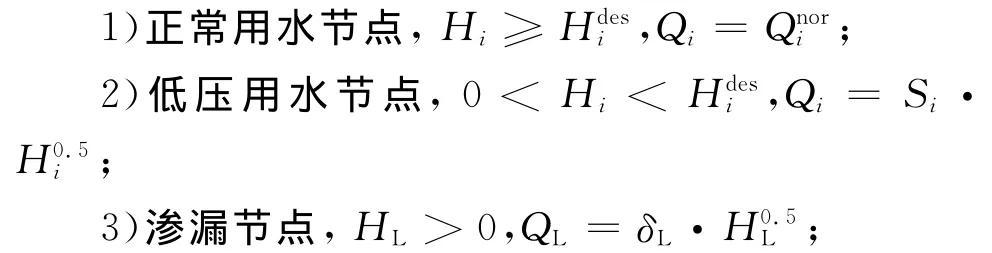
因此,在对渗漏状态下低压供水管网进行水力计算时,可以将上述条件作为判断迭代结束的标准,则利用EPANET实现“分步迭代”水力计算的步骤如下:
1)对管网进行震损评估并在管段中间添加渗漏点,令渗漏点的扩散系数CL=δL。
2)假设所有用水节点为低压用水点,将其替换为喷嘴出流类型并定义扩散系数Ci=Si。
3)调用EPANET进行第一轮迭代计算。
4)校核各用水节点水压,若存在用水节点Hi≥则将该节点修改为正常出流类型,在此过程中仍保持渗漏点的出流类型。
5)调用EPANET对修改后的管网进行第2轮的迭代,若计算结果中所有节点的出流状态都满足条件1)、2)、3)时,则完成水力计算,否则转入第4)步。
4 实例分析
图1为文献[11]中所列供水管网,包括17个管段、10个用水节点、17个虚拟渗漏点(位于各管段中间位置)。该管网由2个水源供水,其中水泵的额定流量及扬程均为720L/s、45m。管网的管段编号、节点编号及当前供水时段的节点流量见图1,管长及管径信息可通过文献[11]获得。分别对该管网在正常供水状态及地震烈度为7、8、9度时进行水力模拟,其中各节点的Hdes=10m,CP=0.3,Cg=1.5,Cy=1.0,根据中国地震烈度表,地震烈度(EI)为7、8、9度 时,地 震峰值 速度v 分 别为130cm/s,250cm/s,500cm/s,模拟结果见图2、3、4。

图1 举例供水管网

图2 不同地震烈度下管段渗漏量
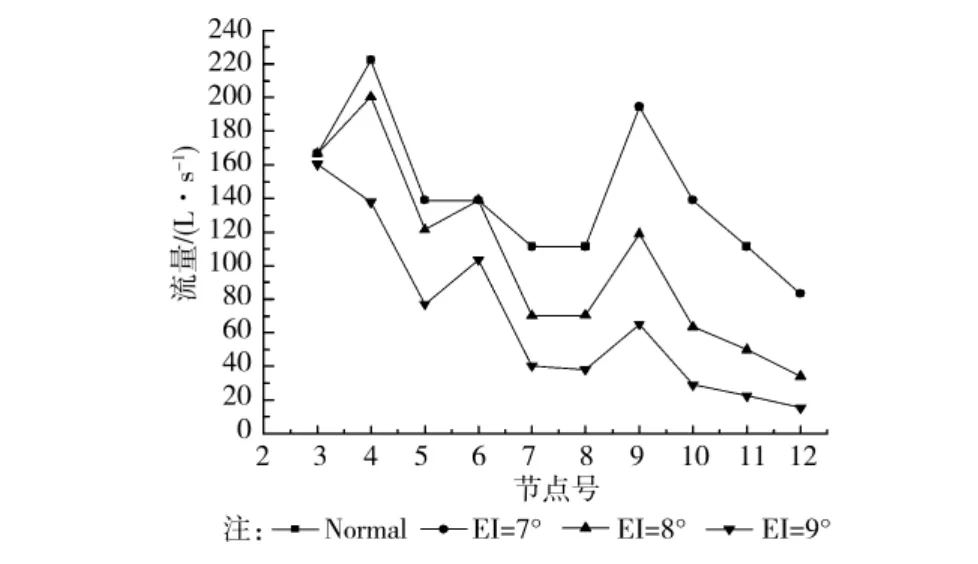
图3 不同地震烈度下节点流量

图4 不同地震烈度下节点水压
当管网在正常状态下运行时,节点12为最不利用水点,其水压约24m。当地震烈度为7度时,管网中部分管段发生渗漏,总体渗漏水平为11.38%,各节点水压均略有下降但仍能保证正常供水。当地震烈度为8度时,管网中各管段都出现不同程度的漏损,总体渗漏水平为52.27%,各节点压力均大幅下降,除了离水源较近的3、6节点外,其它节点均不能保证正常供水。当地震烈度为9度时,管网遭受严重破坏其总体渗漏水平为70.58%,管网末端节点处于无压状态已基本丧失供水能力。通过对比,不同地震烈度下各管段的渗漏程度及渗漏对管网供水能力的影响都不同。如在地震烈度为7度时,管段14的渗漏量最大但并未对管网供水能力造成较大影响,而在地震烈度为8度与9度时,管段3的漏损最大,同时随着管段3、5漏损量的增加,供水管网水压大幅下降,甚至出现瘫痪的状况。总体而言,离水源较近管段的渗漏对管网的影响相对较大,而离水源较远管段的渗漏对管网的影响则相对较小,该结论与实际情况相符。
5 结 论
针对地震导致渗漏的供水管网的水力特性,通过研究分析现有渗漏供水管网的水力模型,在其基础上考虑不同地震烈度下供水管网中各管段的震损失效概率,构建了地震诱发渗漏的供水管网的水力模型。管网的水力模型是非线性的方程组,需要通过迭代求解,为提高水力计算时迭代的收敛速度、避免迭代的发散,并直接应用现有计算软件进行模型求解,笔者提出了适用于低压状态下渗漏供水管网的“分步迭代”水力计算方法。结合EPANET软件,利用构建的模型与提出的方法,实现了不同地震烈度下供水管网中各管段的漏损量、节点压力及流量的预测。预测结果表明,构建的模型和提出的水力计算方法可预测震后管网供水能力。
[1]何维华.汶川“5.12”大地震诱发供水管网等损坏的思考[J].给水排水,2009,35(12):7-11.He W H,Discussion on the water distribution network damage caused by the Wenchuan “5.12”earthquake[J].Water and Wastewater,2009,35(12):7-11.
[2]O'Rourke T D,Beaujon P A,Scawthom C R.Large ground deformations and their effects on lifelines facilities:1906San Francisco earthquake [G]//O'Rourke T D, Hamada M. Case Studies of Liquefaction and Lifeline Performance during Past Earthquakes, NCEER Technical Report 92-0002,1992:130-136.
[3]Lin H.Seismic performance assessment of water delivery systems using GIS technology[D].Memphis:The University of Memphis,1997.
[4]陈玲俐,李杰.供水管网渗漏分析研究[J].地震工程与工程振动,2003,23(1):115-121.Chen L L,Li J.Leakage analysis of water supply network [J].Journal of Earthquake Engineering and Engineering Vibration,2003,23(1):115-121.
[5]周建华,赵洪宾.低水压供水时的管网平差计算方法[J].给水排水,2003,19(3):43-45.Zhou J H,Zhao H B.The study of calculation for pressure driven modeling of water distribution [J].China Water and Wastewater,2003,19(3):43-45.
[6]Soares A K,Reis L F R,Carrijo I B.Head-driven simulation model(HDSM)for water distribution system calibration [J]. Advances in Water Supply Management,Maksimovic,2003(1):197-202.
[7]Cheung P B,van Zyl J E,Reis L F R.Extension of EPANET for pressure driven demand modeling in water distribution system [C]//Proceedings of CCWI 2005-Water Management for the 21st Century,Exeter,UK,2005:215-220.
[8]Wu Z Y,Wang R H,Walski T M,et al.Efficient pressure dependent demand model for large water distribution system analysis[C]//Proceeding of the 8thAnnual Water Distribution System Symposium,Cincinnati,Ohio,USA,2006:27-32.
[9]Liu C G,He S H.Seismic reliability and rehabilitationdecision of water distribution system [J].Transactions of Tianjin University,2010,16(3):223-228.
[10]Pathirana A. EPANET2desktop application for pressure driven demand modeling [C ]//Water Distribution System Analysis 2010,Tucson, AZ,USA,2010.
[11]符圣聪,江静贝,黄世敏.地震时供水管网的可靠性和功能分析[J].工程抗震与加固改造,2007,29(2):95-99.Fu S C,Jiang J B,Huang S M.Reliability and functional analysis of the water supply network in the earthquake[J].Earthquake Resistant Engineering and Retrofitting,2007,29(2):95-99.
[12]American Life Line Alliance. Seismic fragility formulations for water system[R].ASCE,2001.
[13]水道施設耐震工法指針·解説[M].北京:科学出版社,2009.
[14]杨超,蒋健群.城市供水管道震害评估方法的比较与应用[J].城市道桥与防洪,2011,3(3):51-55.Yang C,Jiang J Q.Comparison and application of earthquake damage assessment methods to the urban water distribution system [J].Urban Roads Bridges &Flood Control,2011,3(3):51-55.
[15]李树平.基于EPANET本地化的给水管网教学软件开发 [J].给水排水,2011,37(7):161-164.Li S P.Development of the education software for water supply network based on EPANET localization[J].Water and Wastewater,2011,37(7):161-164.
