输电塔线体系在多维地震激励下的响应分析

田 利，李宏男

（1.山东大学 土建与水利学院，济南 250061；2.大连理工大学 建设工程学部，辽宁 大连 116024）

中国大部分输电线路都要穿越高烈度地震区，地震导致的高压输电塔线体系的破坏时有发生，而且后果极其严重［1－3］。例如，1992 年 的 Landers地震［4］，致使100多条输电线路不同程度损毁，导致洛杉矶电力供应短时瘫痪；1995年日本Kobe地震［5］，总计约有20座输电塔发生基础沉陷，部分绝缘子震坏，地震造成260万用户停电；地震对输电线路破坏最严重的是中国1999年台湾发生的集集地震［3］；2008年四川汶川地震中，据不完全统计［6］，地震导致110kV线路倒塔20多基，500kV茂谭线8基和220kV茂永线2基铁塔损毁。图1给出了汶川地震中输电塔线体系破坏实例图。

图1 汶川地震中输电塔和输电线破坏图

理论研究与震害经验表明，地震时的地面运动是一个复杂的多维运动，包括6个分量，即3个平动分量和3个转动分量［7］。结构在单维与多维地震作用下的响应是不同的，特别是一些复杂工程结构在结构抗震分析中只考虑单分量地震作用是不够的［810］，应该考虑多分量地震作用对结构的影响。近年来学者们对大跨空间结构多维地震分析进行了大量的研究，但对于输电塔线体系多维地震作用下的分析研究甚少。迄今为止的研究如下：李宏男等［11］研究了水平与摇摆地震动作用下输电塔线体系的响应；李保华［12］比较了二维和三维地震动下双塔三线体系的响应；田利等［13］研究了多维地震动分量间相关性和强度比值对输电塔线体系地震响应的影响。以上的研究没有涉及影响体系地震响应的主方向，也没比较体系在单维和多维地震激励下的响应，更没有关于体系地震响应规律。

本文运用非线性时程分析方法，研究了多维地震动对高压输电塔线体系地震响应的影响，本文的多维地震动仅涉及了多维平动分量。根据输电线路实际工程建立了输电塔线体系有限元模型，考虑了输电线的几何非线性；依据《电力设施抗震设计规范》选取了不同场地类型的12条地震波，研究了多维地震动激励下输电塔线体系地震响应规律，可以为输电线路实际工程抗震设计提供指导。

1 高压输电塔线体系有限元模型

以某500kV输电线路实际工程为例，输电模式为双回路四分裂导线布置。塔体为总高度53.9m（呼称高30m）的SZ21型直线塔，档距为400m，最上面是2根地线，下面3层为6根4分裂导线。输电塔的尺寸见图2所示，输电塔主杆件、斜杆和辅助材料分别采用Q345和Q235的角钢，其弹性模量为206GPa。输电线中地线和导线型号分别为LGJ－95／55和LGJ－400／35，输电塔与输电线之间通过悬垂绝缘子连接。利用国际通用有限元程序SAP2000建立精细的输电塔

图2 输电塔尺寸

图3 高压输电塔线耦联体系三维有限元模型

2 多维地震动激励下运动方程

2.1 索的几何刚度矩阵

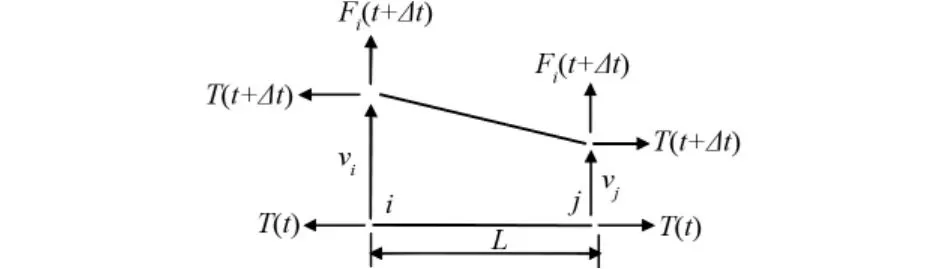
图4 作用在索单元上的力

如图4所示，假设t时刻索单元两节点i、j承受T（t）作用力，长度为L；t＋Δt时刻地震作用下节点i、j承受节点力为Fi（t＋Δt）和Fj（t＋Δt）与T（t＋Δt），索的两端有两个侧向位移vi和vj，达到了一个新的平衡状态状态，这里假定所有向上的力和位移为正。此时，满足力的平衡方程［15］：

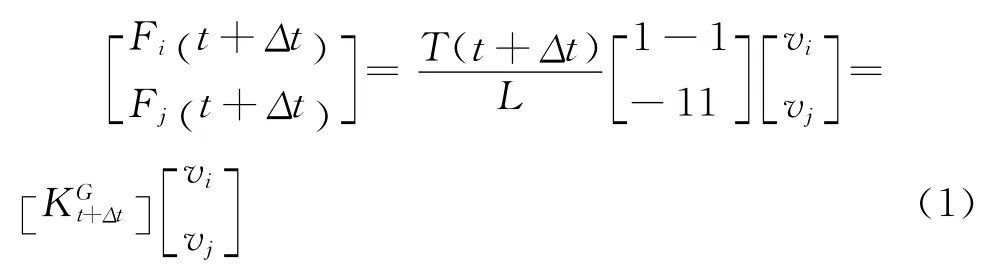
2.2 多维地震作用下输电塔线体系求解方法

输电塔线体系在多维地震作用下，考虑输电线随时间变化刚度矩阵的体系动力平衡方程形式为

式中，［M］为输电线找形完并具有初始刚度时输电塔线体系的质量矩阵，这里忽略了体系质量矩阵随时间的变化；［Kt＋Δt］为输电塔线体系刚度矩阵，是随体系不断变化而变化的；｝、｝和分别是2个水平和1个竖直地震加速度向量；［Ct＋Δt］为输电塔线体系阻尼矩阵，由Rayleigh阻尼可以得到：［Ct＋Δt］＝α［M］＋β［ Kt＋Δt］，可以看出［Ct＋Δt］是随输电塔线体系刚度矩阵变化而变化的；α和β是塔线体系的质量矩阵系数和时变刚度矩阵系数，根据输电线和输电塔的第一频率及其相应阻尼比进行确定。

3 多维地震动的选取

按照中国现行《电力设施抗震设计规范》（GB 50260－96）［16］选取地震记录，对于坚硬、中硬、中软和软土这4类场地，每类场地采用3条不同的地震记录，共计12条地震波。计算时，对多维地震中最大的加速度峰值调整为0.4 g，其余分量按照相应比例进行调整。选取的地震记录情况见表1所示，每类场地的地震动编号分别为①、②和③。

表1 地震记录

4 多维地震激励下输电塔线体系的响应分析

为了研究多维地震动对输电塔线耦联体系地震响应的影响，对图3所示的输电塔线耦联体系施加三维地震激励，采用有限元软件SAP2000进行多维地震动作用下的非线性时程响应分析，时程分析中采用Hilber－Hughes－Taylor逐步积分法，其中输电塔和输电线的阻尼比分别取为0.02和0.01。

4.1 多维地震激励分析工况

顺着输电线方向定义为纵向，垂直输电线方向定义为侧向，竖直方向定义为竖向。对于地震动三维分量中地震波峰值最大的分量定义为分量1，与分量1水平垂直的分量定义为分量2，竖直分量定义为分量3。

表2给出了地震动激励工况，共7种。工况1为分量1对体系纵向激励，工况2为分量1对体系纵向激励，目的是为了比较体系纵向和侧向在地震激励下的响应；工况3为分量1对体系纵向激励，工况4为分量2对体系侧向激励，工况5为分量3对体系竖向激励，工况6为分量1和2共同对体系纵和侧向激励，工况7为分量1、2和3共同对体系纵、侧和竖向激励，目的是比较单维激励、双向水平激励和三维激励下的体系响应。

表2 地震动激励工况

4.2 多维地震激励下输电塔的地震响应分析

首先，分别计算了分量1对体系纵向激励（工况1）和分量1对体系纵向激励（工况2）下地震的响应，图5给出了纵向和侧向激励下输电塔底部内力最大值的比较情况。可以看出地震波不同，比值不同，但纵向激励得到的内力均大于侧向激励的，因此要得到输电塔内力最大值，三维地震分量中地震波峰值最大的分量（分量1）应该沿着体系纵向输入。对于以下的分析，均假设分量1的方向与体系的纵向一致，分量2的方向与体系的侧向一致，分量3的方向与体系的竖向一致。

图5 输电塔底部内力响应比较

图6 输电塔底部杆件的轴力响应比较

图6给出了输电塔底部杆件的轴力在纵向（工况3）、侧向（工况4）、竖向（工况5）和双向水平（工况6）地震激励下与三维（工况7）地震激励下的比较。纵向激励与三维地震激励的轴力比值在0.787～0.935之间，说明对于输电塔内力的响应，纵向地震激励在三维地震激励中起到主导作用；侧向地震激励与三维地震激励的轴力比值在0.364～0.691之间，说明其在三维地震激励中的影响小于纵向激励的；竖向地震激励与三维地震激励的轴力比值在0.150～0.483之间，说明其在三维地震激励中的影响最小；双向水平地震激励与三维地震激励的比值为1，说明考虑双向水平共同地震激励就能得到输电塔内力的最大值。

通过以上对输电塔的地震响应分析，可以得到结论：纵向地震激励对输电塔的内力响应起主导作用，侧向地震激励次之，竖向地震激励最小；并且考虑双向水平地震激励可以得到输电塔内力最大值。

根据以上的分析，纵向地震激励下输电塔内力响应与三维地震激励的比值分布在0.787～0.935之间，分布区间小于其它单独激励情况下的，并且纵向地震激励在三维地震激励中起到主导作用。因此，选用纵向地震激励下的不同高度处输电塔轴力最大值与三维地震激励下的进行拟合，这里定义

式中：Rxyz－max为三维地震激励下输电塔轴力的最大值；Rx－max为纵向地震激励下输电塔轴力的最大值；γ是拟合系数。表3中给出四类场地中的3地震波的拟合系数，按照场地对其进行平均，得到γ的均值分布在1.1～1.2之间。图7给出了拟合值与最大值之间的比较，即纵向地震激励下轴力最大值乘以拟合系数与三维地震激励下轴力最大值之间的比较，可以看出不同高度处轴力吻合的较好。如果已知纵向地震激励下输电塔轴力的最大值，根据以上的公式，可以粗略估算出三维地震激励下输电塔轴力的最大值。为了便于工程的应用，表4给出了输电塔的轴力方差比值，并给出了不同场地上的平均值。

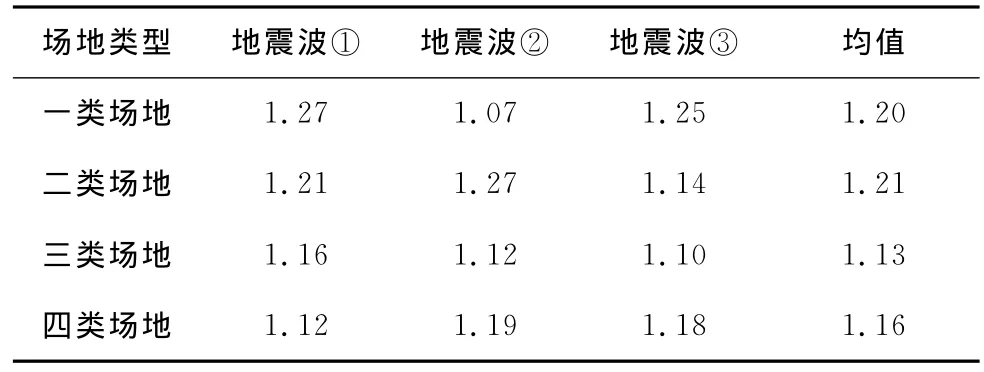
表3 拟合系数

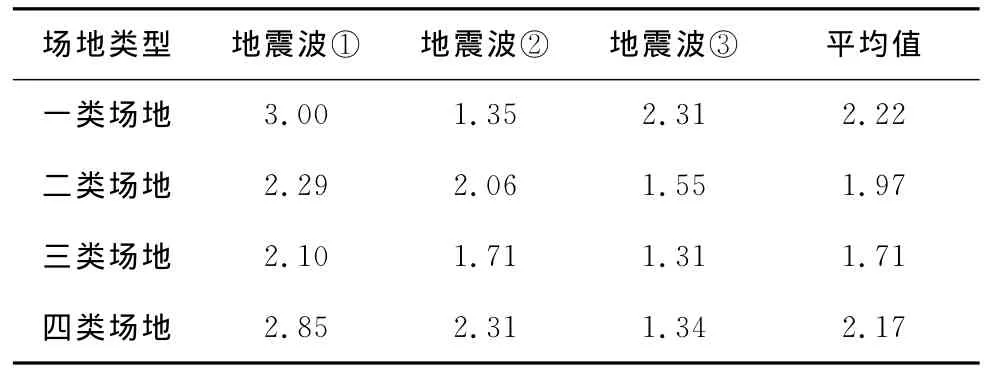
表4 输电塔的轴力方差比值

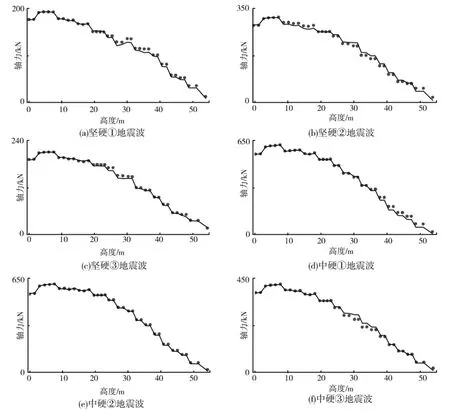
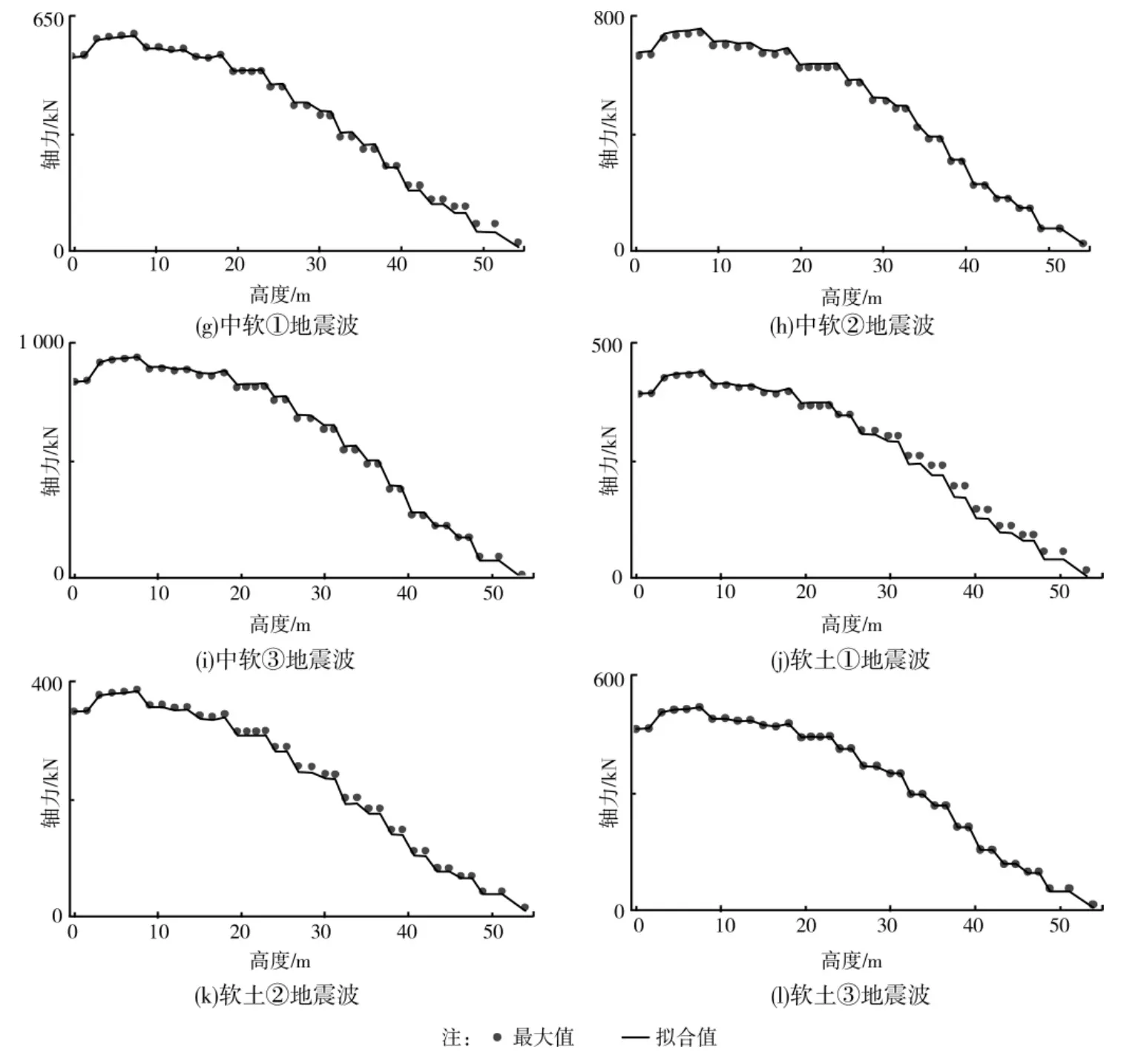
图7 拟合值与最大值的比较

图8 输电线张力误差比较

4.3 多维地震激励下输电线的地震响应分析

图8给出了输电线在纵向（工况3）、侧向（工况4）、竖向（工况5）和双向水平（工况6）地震激励下与三维（工况7）地震激励下的张力误差比较。纵向地震激励与三维地震激励的输电线张力误差较小，最大仅为5.5%，说明对于输电线的张力，仅考虑纵向地震激励就能满足工程设计要求。侧向地震激励与三维地震激励的输电线张力误差随着场地类型的不同变化很大，一类场地的误差在10%以内，二类和四类场地的误差在10%～20%之间，三类场地的误差在20%～40%之间。竖向地震激励与三维地震激励的输电线张力误差随着场地类型的不同变化也很大，基本规律与侧向地震激励与三维地震激励的张力误差变化相似。双向水平地震激励与三维地震激励的输电线张力误差很小，最大仅为2.1%，可以忽略不计，说明考虑双向水平地震激励可以得到输电线张力的最大值。

图9给出了各类场地不同地震激励工况（工况3、工况4、工况5、工况6和工况7）下输电线的纵向位移最大值变化曲线，其形状为“斜直线”。当仅考虑侧向或竖向地震激励，输电线纵向位移几乎为零，说明纵向位移受侧向或竖向地震激励的影响很小，可以忽略不计；仅考虑纵向地震激励得到的纵向位移几乎与考虑双向水平或三向地震共同激励的纵向位移重合，说明其余两方向地震激励与输电线的纵向响应耦合很小。因此仅考虑纵向激励就可以得到输电线纵向位移的最大值。

图9 不同工况激励下输电线纵向位移

图10给出了各类场地不同地震激励工况（工况3、工况4、工况5、工况6和工况7）下输电线的侧向位移最大值变化曲线，其大小和形状受地震波的影响较大，侧向位移最大值大多数情况下出现在跨中，形状有“锯齿形”、“半圆形”等。由图可以看出仅考虑纵向或竖向地震激励，输电线侧向位移接近于零，说明侧向位移受纵向或竖向地震激励的影响很小，可以忽略不计；仅考虑侧向地震激励得到的侧向位移几乎与考虑水平双向或三向地震共同激励的侧向位移重合，说明其余两方向地震激励与输电线的侧向响应耦合很小。因此仅考虑侧向激励就可以得到输电线侧向位移的最大值。

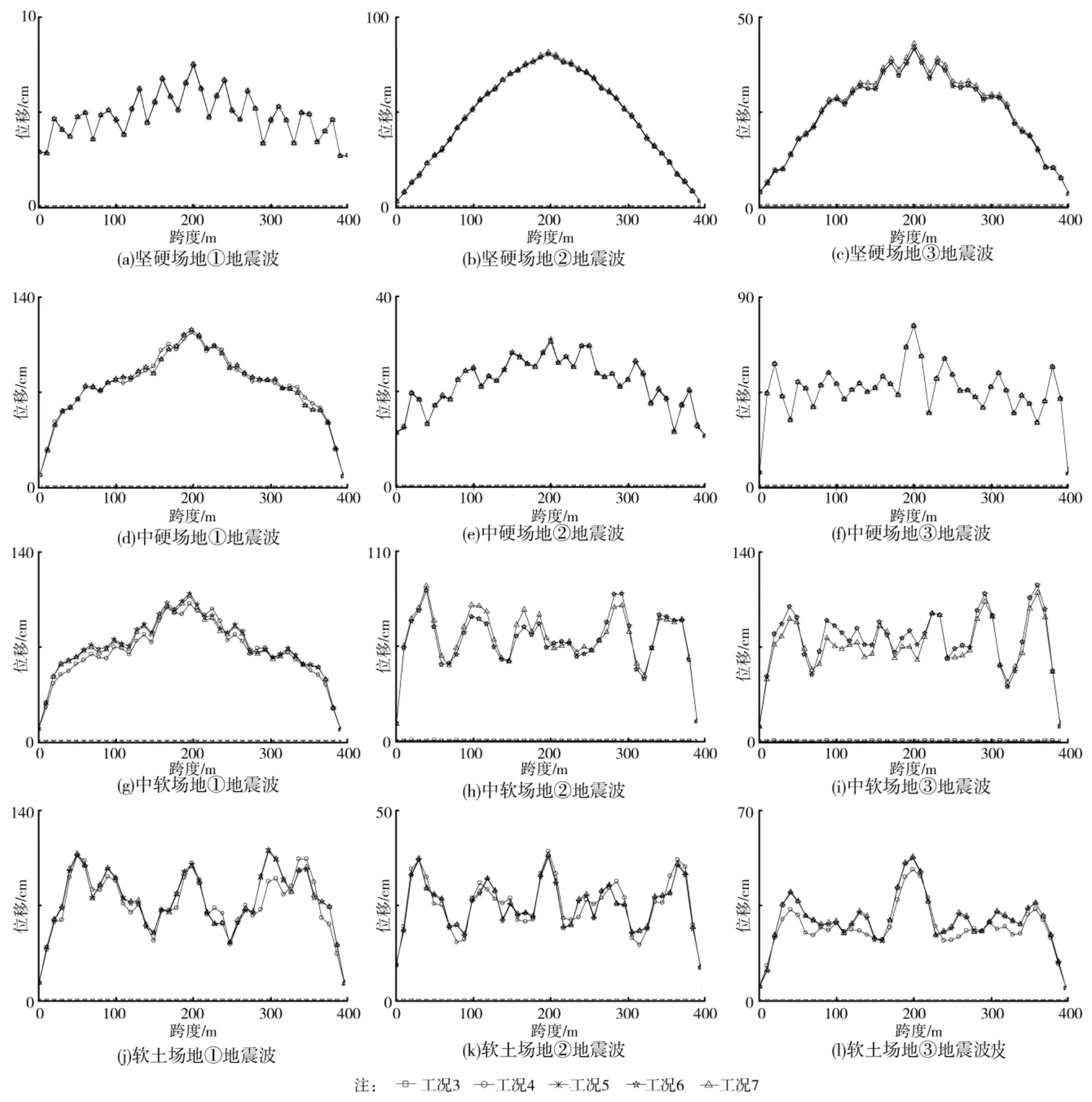
图10 不同工况激励下输电线侧向位移

图11给出了各类场地不同地震激励工况（工况3、工况4、工况5、工况6和工况7）下输电线的竖向位移最大值变化曲线，其形状受地震波的影响很大，没有规律性。由图可以看出仅考虑纵向、侧向或水平双向地震共同激励得到的输电线竖向位移有可能大于仅考虑竖向地震激励，说明竖向位移受纵向或侧向地震的影响很大；考虑三向地震共同激励得到的竖向位移要大于或远大于仅考虑竖向地震激励的，并且三向地震共同激励得到的竖向位移是所有工况中的最大值，说明其余两方向地震激励与输电线的竖向响应耦合很大。因此要得到输电线竖向位移的最大值，应该考虑三维地震共同激励。

5 结语

以某500kV输电线路实际工程为背景，建立了输电塔线体系三维有限元模型，利用数值模拟研究了多维地震激励下高压输电塔线体系地震响应规律。

1）纵向地震激励对输电塔的内力响应起主导作用，侧向次之，竖向最小，并且考虑双向水平地震共同激励可以得到输电塔内力最大值。

2）通过拟合纵向地震作用下输电塔轴力最大值与三维地震作用下的轴力最大值，得到了拟合系数为1.1～1.2，可供输电线路实际工程设计参考；为了便于工程应用，给出了输电塔的轴力方差比值。

3）仅考虑纵向地震激励就能得到满足工程设计要求的输电线张力值，考虑双向水平地震激励可以得到输电线张力的最大值；仅考虑纵向地震激励可以得到输电线纵向位移最大值，仅考虑侧向地震激励可以得到输电线侧向位移最大值，但对于输电线竖向位移最大值应考虑三维地震共同作用。

4）在输电塔线体系的分析和设计中应考虑三维地震共同作用，进而确保输电线路经历地震时的安全运行。

［1］李宏男，王前信.大跨越输电塔体系的动力特性［J］.土木工程学报，1997，30（5）：28－36.Li H N，Wang Q X.Dynamic characteristics of longspan transmission lines and their supporting towers［J］.China Civil Engineering Journal，1997，30（5）：28－36.

［2］谢强，李杰.电力系统自然灾害的现状与对策［J］.自然灾害学报，2006，15（4）：126－131.Xie Q，Li J.Current situation of natural disaster in electric power system and counterm easures［J］.Journal of Natural Disasters，2006，15（4）：126－131.

［3］尹荣华，李东亮，刘戈林，等.高压输电塔震害及抗震研究［J］.世界地震工程，2005，21（1）：51－54.Yin R H，Li D L，Liu G L，et al.Seismic damage and analysis of power transmission towers［J］. World Earthquake Engineering，2005，21（1）：51－54.

［4］Hall F J.Northridge earthquake of January 17，1994：reconnaissance report［J］.Earthquake Spectral，1995，11（3）：212－215.

［5］Shinozuka M. The Hanshin－Awaji earthquake of January 17，1994：performance of lifelines［R］.State University of New York at Buffalo，NCEER report：95－0015.

［6］张子引，赵彪，曹伟炜.四川汶川8.0级地震电网受灾情况调研与初步分析［J］.电力技术经济，2008，20（4）：1－4.Zhang Z Y，Zhao B，Cao W W.Investigation and preliminary analysis of damages on the power grid in the Wenchuan earthquake of M8.0 ［J］.Electric Power Technologic Economics，2008，20（4）：1－4.

［7］李宏男.结构多维抗震理论［M］.北京：科学出版社，2006.

［8］薛素铎，曹资.多维地震作用下网壳结构的随机分析方法［J］.空间结构，2002，8（1）：44－51.Xue S D，Cao Z.Random analysis method for lattice shells under multiple earthquake excitaitons［J］.Spatial Structures，2002，8（1）：44－51.

［9］易方民，高小旺.高层建筑钢结构在多维地震动输入作用下的反应［J］.建筑结构学报，2003，24（3）：33－43.Yi F M，Gao X W.Response of tall－building steel structure to multi－dimensional seismic action ［J］.Journal of Building Structires，2003，24（3）：33－43.

［10］张爱林，张传成，刘学春.多维地震输入下首都机场航站楼T3反应谱分析［J］.地震工程与工程振动，2008，28（1）：32－37.Zhang A L，Zhang C C，Liu X C，et al.The response spectrum analysis of terminal building of Beijing capital airport under multi－dimensional earthquake input ［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28（1）：32－37.

［11］李宏男，王前信.水平与摇摆地震动作用下大跨越输电塔体系的反应分析［J］.工程力学，1991，8（4）：68－79.Li H N，Wang Q X.Response analysis of the system xonsisting of long span transmission lines and their supporting towers to horizontal and rocking seismic motions［J］.Engineering Mechanics，1991，8（4）：68－79.

［12］李保华.输电塔线体系多维地震反应分析［D］.哈尔滨：哈尔滨工业大学，2007.

［13］Tian L，Li H N.Parametric study of seismic response of transmission tower－line system subjected to multicomponent earthquake excitations［C］／／Earth ＆ Space Conference，ASCE，Hawaii，America，2010：2925－2932.

［14］沈世钊，徐崇宝，赵臣.悬索结构设计［M］.北京：中国建筑工业出版社，1997.

［15］Wilson E L.Three dimensional static and dynamic analysis of structures：aphysical approach with emphasis on earthquake engineering ［M］.Computers and Structures，Inc，Berkley，California，2002.

［16］GB 50260－96电力设施抗震设计规范［S］.北京：1996.