正项级数敛散性判别的一种新方法

吴国磊

(如皋高等师范学校 数理与信息技术系，江苏 如皋 226500)

0 引言

众所周知，级数是微积分学中的重要的内容，对于数项级数敛散性的判别，通常我们总是先判定它是否是绝对收敛，而判定绝对收敛的本质就是判别正项级数的收敛性.正项级数的判别法，常见的有D＇Alembert判别法、Cauchy判别法、Raabe对数判别法和Gauss判别法等，但都有一定的局限性，很多学者在此基础上进行了改进，如文献［1］—［5］，事实上，我们可以根据Raabe判别法，给出了一个与其类似的新判别法.

1 已有相关研究

1.1 Raabe判别法

该判别法和如下形式是等价的:

1.2 Gauss判别法

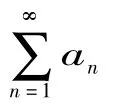
其中λ，μ是常数，而θn是有界量: θn≤L;那么，

(1)如果λ＞1或λ=1，μ＞1级数收敛;(2)如果λ＜1或λ=1，μ＜1级数发散.

1.3 一个引理

2 Raabe判别法的推广

2.1 Raabe判别法的第一步改进

王晖东、刘笑颖［8］已经对Raabe判别法进行过改进，如下:

证明:当n→∞ 时，有

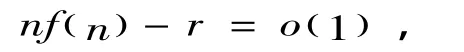
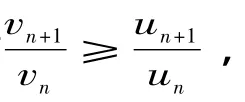
2.2 Raabe判别法的两步改进

进一步的改进，可得两步改进方法:

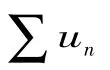
王晖东、刘笑颖对Raabe判别法进行改进仅限于此，若将上述两个定理进行再次推广，可以得到如下的新方法.

2.3 Raabe判别法的多步改进

证明:当n→∞ 时，有

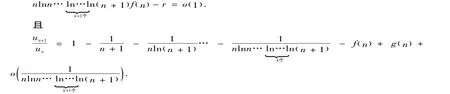
再使用数学归纳法，当m=1时，

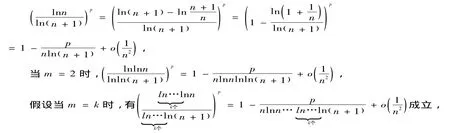
则当m=k+1时，有

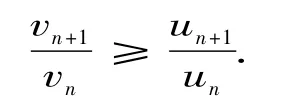
2.4 Raabe判别法的多步改进的实效举例

此时，为了方便描述，令

现在将式子如下展开

此时，如果取r＞1，则g(n)＞0;如果取r＜1，则g(n)＜0，此时该判别法失效.我们用更进一步的改进定理来判断其收敛性.这时有

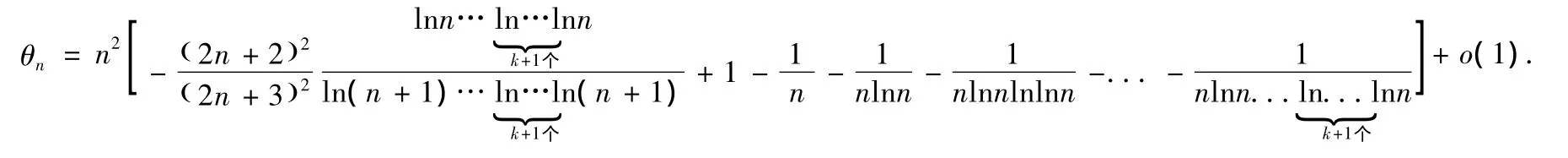
此时，如果取0＜r＜1，则g(n)≥0，则该级数发散.

［1］杨钟玄.正项级数敛散性的一个新判别法［J］.四川师范大学学报(自然科学版)，2005，28(6):667－670.

［2］洪勇.一个新的正项级数敛散性判别定理及应用［J］.四川师范大学学报(自然科学版)，2004，27(3):245－247.

［3］高原，刘大彬.关于正项级数敛散性判定的一种方法［J］.齐齐哈尔大学学报，2011，27(4):86－88.

［4］张永明.正项级数收敛性的一种新的判别法［J］.数学的实践与认识，2004，34(1):173－176.

［5］王炳安，李淑敏.关于正项级数的一组收敛性判别法［J］.大连大学学报，2004，25(4):1－5.

［6］陈纪修，於崇华，金路.《数学分析》第二版［M］.高等教育出版社，2004.22－23.

［7］童小龙.Gauss判别法的改进［J］.中国矿业大学(北京)(博士专家论坛)，2008:352－353.

［8］王晖东，刘笑颖.拉贝判别法的推广［J］.大学数学，2011，27(4):165 －170.

［责任编辑:闫 昕］