基于Elman动态神经网络的煤质预测算法研究

张 玮，张 丹

（华北科技学院教务处，北京101601）

煤炭在我国一次能源的生产和消费结构中，占有举足轻重的地位。整个“十一五”期间，煤炭消费的年均增幅达到3.02%，截至2010年，煤炭的消费量已接近总量的74%［1］。然而，我国煤炭普遍属于中灰、中疏煤，煤中的灰分一般为10%～20%，含硫量在1.0%～2.8%，煤炭在消费使用过程中会对环境造成严重的污染。随着市场需求的改变以及整个社会环境安全意识的增强，煤炭产品的质量要求正在被不断提高。在此背景下，选煤厂唯有加快技术进步的速度，积极落实洁净煤技术，下狠心淘汰落后设备，不断提高产品质量，方能适应国内外市场的需求，实现企业的可持续发展。

配煤过程依据用户提出的煤质指标，将多种不同性质的煤种按一定比例进行合理混配，实现煤质互补、提高燃煤效率、减少污染，是当前合理利用煤炭资源的一种重要手段。如何准确预测配煤煤质是整个配煤过程的关键环节，诸多研究表明：单煤种的性能对于配煤后的煤质具有复杂的非线性影响［2－3］，很难建立精确的配煤煤质预测数学模型。而人工神经网络在复杂非线性问题的数学建模上具有显著优势，能高精度的重现非线性连续函数。为此，基于人工Elman神经网络，本文在实验基础上，建立了配煤煤质预测模型，实现了对配煤煤质的准确预测。

1 构建原理

目前，用于煤矿企业设备组网的前馈BP神经网络，属于典型的非线性静态映射，通过简单的非线性单元的组合映射，来模拟复杂的非线性问题，具有结构简单、可靠性高的特点［4，8－9］。但是，由于静态非线性映射自身缺乏丰富的动力学规则，导致BP网络在煤炭企业实际组网应用中，普遍存在运算速度慢、目标函数在局部极小值处易陷入死循环等问题。煤矿井下复杂恶劣工作环境，决定了井下自动化控制网络必须具有高度的自主性和稳定性，能及时对各种突发状况做出准确的反应，BP神经网络在此方面难以满足要求。Elman动态回归神经网络沿用了BP网络的基本结构，重点是在隐含层后增加一个充当延时算子的承接层，借此完成对控制数据的中继记忆，令整个控制系统得以应对短时间大量数据爆发式出现的突发状况，增强了煤矿设备控制网络的全局稳定性，使得网络系统得以准确地反应井下设备的实时动态特性［4］。同时，处理单元的增多，使其具有了更强大的运算功能，极大缩短了问题处理的效率。鉴于此，基于Elman反馈型神经网络，我们设计了配煤煤质的预测模型，以发热量、水分、灰分以及挥发分为评价指标，利用Elman动态神经网络模型，对配煤所得复煤的品质进行预测。

1.1 反馈型Elman神经网络结构

神经网络模型含有输入层、隐含层、关联层（承接层）和输出层这4层结构。运算时，隐含层的输出量先被载入承接层进行延迟存储，之后与导入隐含层的输入量进行自关联，内建了一个反馈网络。这样做，一方面通过数据的自检比对，提高了数据的准确性；另一方面提高了动态信息的处理能力，非常适合用于搭建煤矿企业井下控制网络。

1.2 网络的学习训练模式

Elman神经网络的非线性模型定义为［5］：

式中，λ为Elman神经网络的连接权矩阵（λ1：输入层到隐含层，λ2：隐含层到承接层，λ3：隐含层到输出层）；M（n）和Me（n）分别为隐含层和承接层的输出量；N（n）为输出层的输出量；k（0≤k≤1）是自连接反馈增益因子；u（）是隐含层、关联层输出量的线性组合；e［］为隐含层与承接层的传递函数；f［］为输出层的传递函数，均为sigmoid型神经元非线性作用函数，其形式为：

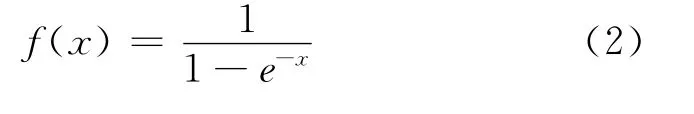
模型建立后，利用自适应动量梯度降低算法训练网络，调整函数权值和阈值参数，减低误差。权值和阈值等参数确定后，便可进行测试。

2 配煤煤质预测模型的建立

2.1 选取检测样本

以某集团为例，其产品主要有15种单一煤种、4种混合煤种，配煤厂的目标配煤精度小于1%，复煤的煤质要求如表1所示。本研究将应用根据上述原理建立的反馈型Elman模型，对配煤的煤质开展预测。

表1 配煤后复煤的煤质目标

以试验获得的部分典型单一煤质性能数据为参考［6－7］，利用模型预测配煤煤质。研究中，选取了14组数据来进行模型的预测，其中前12组作为网络的训练样本，后2组数据作为检测样本。预测样本的设计过程以检测样本的数据加以描述，输入量是单一煤种1、2和3号的煤质数据，输出量是配煤的煤质数据。样本数据信息如表2所示。

表2 检测样本数据

2.2 模型架构

由表2可知，预测模型的输入层含有单一煤种的发热量（Cad）、水分（Aad）、灰分（Vad）、挥发分（Mad）这五个输入量，预测中4种单一煤种为一组，模型中每组具有16个输入层节点，输出层具有4个节点，对应配煤的发热量、水分、灰分、挥发分这四个煤质指标。

整个配煤煤质预测模型设计中隐含层节点数目的选，择取决于煤种的复杂程度以及具体配煤操作。参考相关研究中确定隐含层节点数的方法［6］。

式中：ψ为配煤数据样本数；输入层的神经元节点数为n，ni则为隐层神经元节点数。

如果i＞ni＝0。隐含层作用函数为正切sigmoid神经元非线性函数，输出层作用函数为正切sigmoid神经元线性函数。在此基础上，综合考虑网络的运算性能，最终确定网络隐含层节点数为26个，组建（16，26，4）型Elman动态神经网络。

2.3 网络训练与精度效验

随即选取18组配煤数据样本进行网络训练与精度效验，使用16组数据样本进行网络训练，最后2组样本用于精度效验，部分样本信息如表3所示。同时，需要对用于训练学习的样本进行归一化处理，以提高网络的收敛性。这里我们采用了学习速率自适应的梯度下降算法，对Elman网络模型进行学习训练。训练参数被设置为：网络的训练次数为5000，学习动量因子为0.80，学习速率为0.05，学习结束时的目标平均误差为0.001，其他参数直接选择默认值。

研究中，通过实验数据与模型预测结果的比对，如表3所示，计算得出网络的预测精度为0.000995371。说明本预测模型设计合理，对于配煤后的煤质具有良好的预测准确性，以反馈型Elman神经网络进行煤质预测是可行的，其精度满足选煤厂的控制要求。

表3 实验结果与预测结果比较

3 结语

通过配煤所得复煤的多种煤质指标，与其所含的单一煤种之间具有复杂的非线性关系。对于选煤厂而言，必须建立高精度的煤质预测分析模型，准确把握配煤煤质情况。本文利用动态Elman神经网络构建配煤煤质预测模型，极大程度的提高了模型的冗余度，增强了应对突发位置状况的能力，提高了预测的准确性与速度，降低了选煤厂的人力和物力投入，提高了企业的经济效益。与此同时，进一步充实了配煤的基础理论研究，促进了配煤预测技术的发展与完善，对于相关研究起到了借鉴作用。

［1］李颖.基于非线性理论的动力配煤模型的研究［D］.杭州：浙江大学，2002.

［2］孙庶.动力配煤几个主要煤质指标可加性的论证［J］.煤炭技术，2009（5）：164－166.

［3］侯静，赵益坤.动力配煤的数学模型及优化解［J］.太原理工大学学报，2006（4）：486－488.

［4］邓俊，赖旭芝，吴敏.基于神经网络和模拟退火算法的配煤智能优化方法选煤技术［J］.冶金自动化，2007（3）：19－23.

［5］常爱英，吴铁军，包鑫.基于最小二乘支持向量机的动力配煤着火特性预测模型［J］.煤炭学报，2010（8）：1380－1383.

［6］AT ＆ T Bell Labs，Holmdel，NJ，07733，USA.AT ＆ T Bell Labs，Holmdel，NJ，07733，USA［J］.AT ＆ T Bell Labs，2005（9）.

［7］刘泽常，高洪阁.动力配煤主要煤质指标可加性的统计验证［J］.煤炭加工与综合利用，1999（5）：1－3.

［8］付胜，庞印华.基于线性优化算法的自动配煤控制系统设计［J］.中国煤炭，2011（2）：66－69.

［9］袁曾任.人工神经元网络及其应用［M］.北京：清华大学出版社，1999.