任意数列一般项公式的证明与应用
2013-11-19徐望斌余盛利
湖北师范大学学报(自然科学版) 2013年2期
徐望斌,余盛利
(湖北师范学院 数学与统计学院,湖北 黄石 435002)
0 引言
对数列一般项的研究是认识数列的基本方法。《初等代数研究》(下册)给出了任意数列一般项公式,并用数学归纳法进行了证明。这种证明方法并未揭示该公式的本质,因而不利于学生的理解和掌握。为此,本文给出任意数列一般项公式的另一种证明,并用此公式证明了k阶等差数列前n项和公式。
本文的基础概念是数列的差分,对任意数列{un},数列的一阶差分△u1=u2-u1,k阶差分△ku1=△(△k-1u1) ,k,n为正整数。并有基本结论:
(1)
1 定理及其证明
定理1 对任意数列{un},都有
(2)
证明 根据(1) 式变形(2) 式右边

(3)
(3)式子中的uk(1≤k
(4)
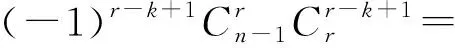
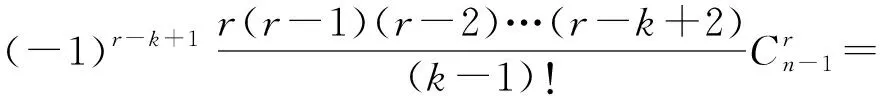
……………………………………………………=
(4)变形为

2 定理的应用
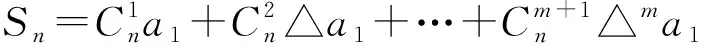
证明 {an} 的前n项和Sn构成数列{Sn} ,由定理1知
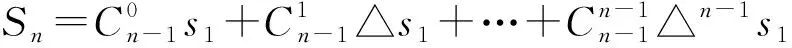
(5)
s1=a1,△s1=s2-s1=a2,△2s1=△a2,…,△n-1s1=△n-2a2
∵{an} 是m阶等差数列, ∴△m+1a2=△m+2a2=…=△n-2a2=0.
(5) 变形为
(6)
对(6) 式右边的每一项逐次进行添项、减项、合并变形:
…………………………………………………………
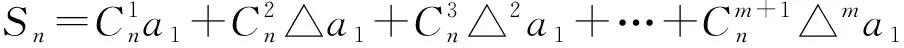
参考文献:
[1]余元希,田万海.初等代数研究(下册)[M].北京:高等教育出版社,2004.
[2]刘纯刚,许丽利.关于 k阶等差数列通项 an及前n 项和Sn的讨论[J].鸡西大学学报,2004,4(6):39~40.
