一类阶段结构和B-D功能性反应的三种群顺环捕食系统

晋金才，窦霁虹，杨建飞

（1.西安邮电大学 电子工程学院，陕西西安 710121；2.西北大学 数学系，陕西西安 710127；3.西北大学 经济管理学院，陕西西安 710127）

在生物数学中，具有阶段结构或者具有功能性反应的生物数学模型被研究者所重视[1-9]，文献[1]研究了具有Beddington-DeAngelis功能性反应的三维顺环捕食系统，得到了系统一致持续生存、存在唯一全局渐近稳定正周期解与概周期解的充分条件，文献[2,10]研究了食饵具有阶段结构和Beddington-DeAngelis功能性反应的两种群食饵-捕食者模型的持久性和周期解的存在性。本文对一类同时具有阶段结构和Beddington-DeAngelis功能性反应的非自治三种群顺环捕食系统进行研究①。

1 数学模型

本文研究了一类具有阶段结构和Beddington-DeAngelis功能性反应的非自治三种群顺环捕食系统②，即

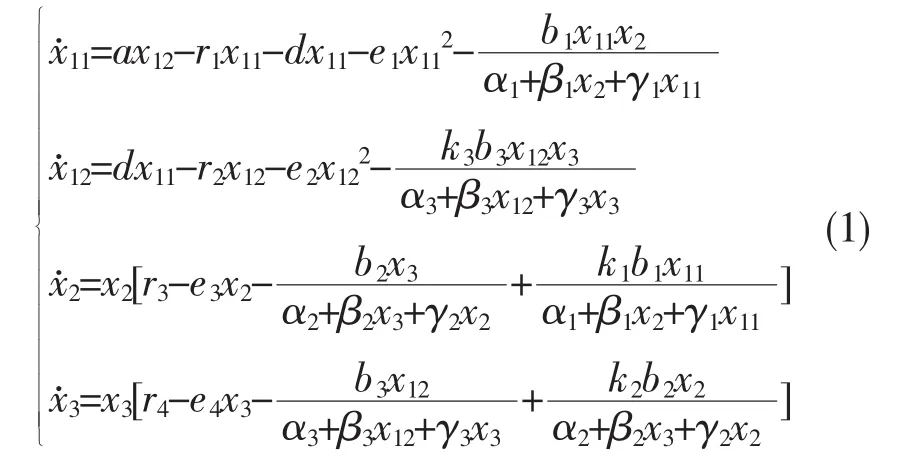
其中 x11(t)，x12(t)，x2(t)，x3(t)分别表示种群 1 的幼年个体和成年个体及种群2,种群3在t时刻的种群密度，幼年个体x11(t)不能捕食x3(t)，成年个体 x12(t)捕食 x2(t)，x2(t)捕食 x3(t)，x3(t)捕食幼年个体x11(t)，ri(t),i=1,2,3,4为种群的死亡率，a(t)为成年个体对新生幼年个体的转化系数，d(t)为幼年个体向成年个体的转化系数，ei(t),i=1,2,3,4为密度制约系数。这里所有系数都是关于t函数，比如a=a(t))，且都是定义在[0,+∞]上连续的正周期函数，并记

定义1[1]对于系统的任意正解(x11(t),x12(t)，x2(t),x3(t)),若存在实数M≥m＞0满足

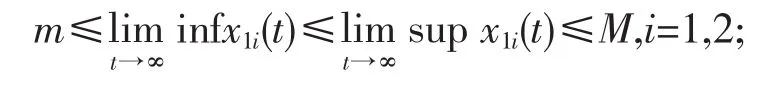
引理1[5]若微分不等式满足y(t)(p-qy(t))，y(t)=x(0),其中 p，q 是常数，则其解满足不等式

引理2[11](Brouwer不动点定理)假设中的有界闭凸集，T∈C(Ω,Ω)，则存在 X0∈Ω，使得TX0=X0。

引理3[12]设f（x）为定义在[0，+∞]上的非负可微函数，若有界，则为一常数，且有

2 定理及其证明

定理1如果系统(1)的解满足初值条件xli(0)＞0，xj(0)＞0，i=1，2，j=2，3 那么系统(1)的所有满足初值条件解最终都满足xli（t）＞0，xj(t)＞0,i=1，2，j=2，3。

证明 因为

由比较定理知

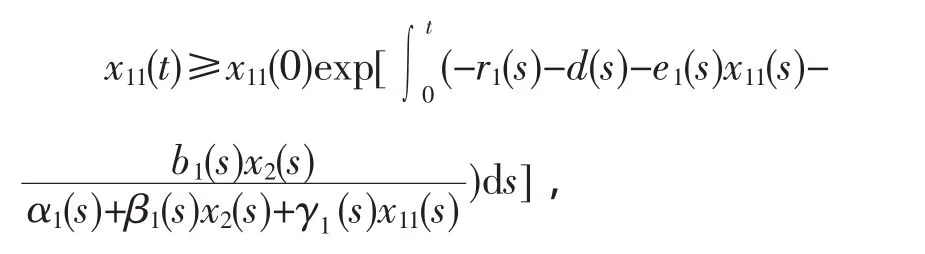
由生物学意义知 x11(0)＞0，则 x11(t)＞0；同理知x12(t)＞0。

又由于

由生物学意义知 x2(0)＞0，则 x2(t)＞0；同理知x3(t)＞0，故定理 1 成立。

定理2 如果系统(1)满足条件

那么系统(1)是一致持续生存的。

证明 取函数S(t)=x11(t)+x12(t)，则S(t)沿系统(1)的导函数是

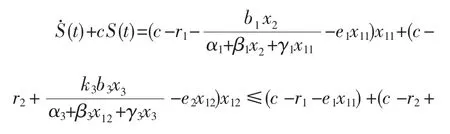
则对于常数c，有

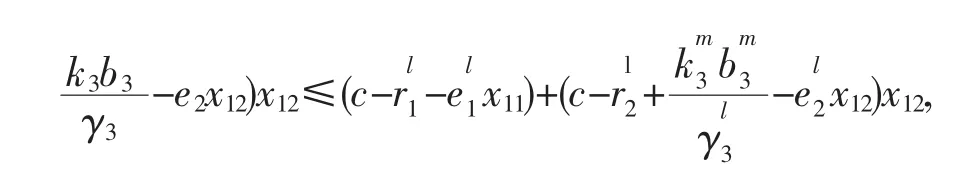
由系统的后两个方程及xj(t)＞0,j=2，3则，取实数

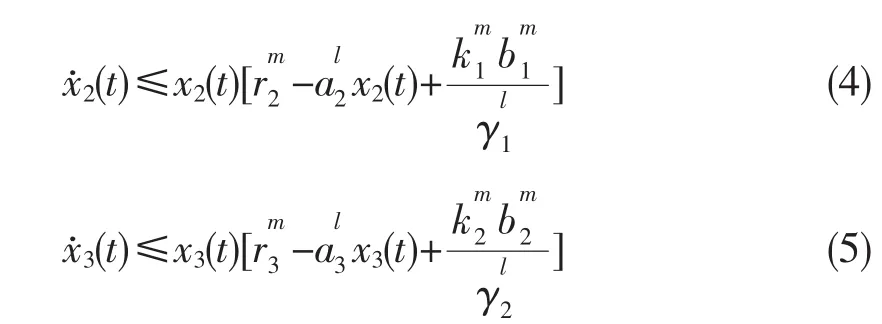
对(1)，(2)两式从 0 到 t积分得

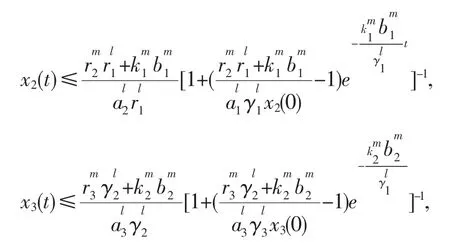
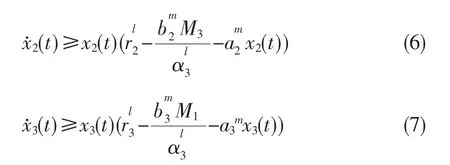
同理可知存在 mj＞0，j=2,3，使得 xj(t)≥mj，j=2,3。

令 V(t)=min{x11(t),x12(t)}，当 x11(t)≤x12(t)时，则V(t)沿系统的右上导数为

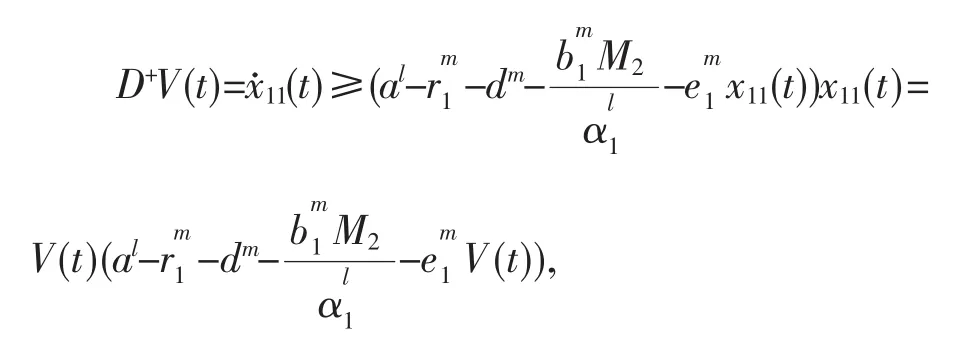
当 x11(t)≥x12(t)时，

定理3 如果系统(1)满足定理2的条件，并且满足

那么系统(1)唯一存在全局渐近稳定的周期正解。

如果X0∈Ω0，则由解对初值的连续依赖性定理知，T关于X0在Ω0上是连续的，并且X0∈Ω0一定有令 t=ω，则有 x(t+t0,t0X0)∈Ω0，也就是TΩ0∈Ω0由引理2知，映射T在Ω0中至少存在一个不动点X0，即系统(2)至少存在一个周期解。设为Y(t)=(y11(t),y12(t),y2(t),y3(t),y1i(t)＞0，i=1，2，j=2，3）为系统(1)的周期解，X(t)为系统(1)满足初值 x1i(0)＞0,xj(0)＞0,i=1,2,j=2，3 的任意解，构造函数：

则W(t)沿系统(1)正解的右上导数是

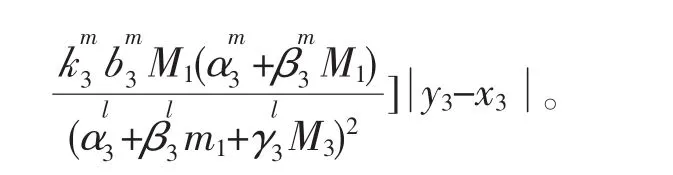
取常数β使

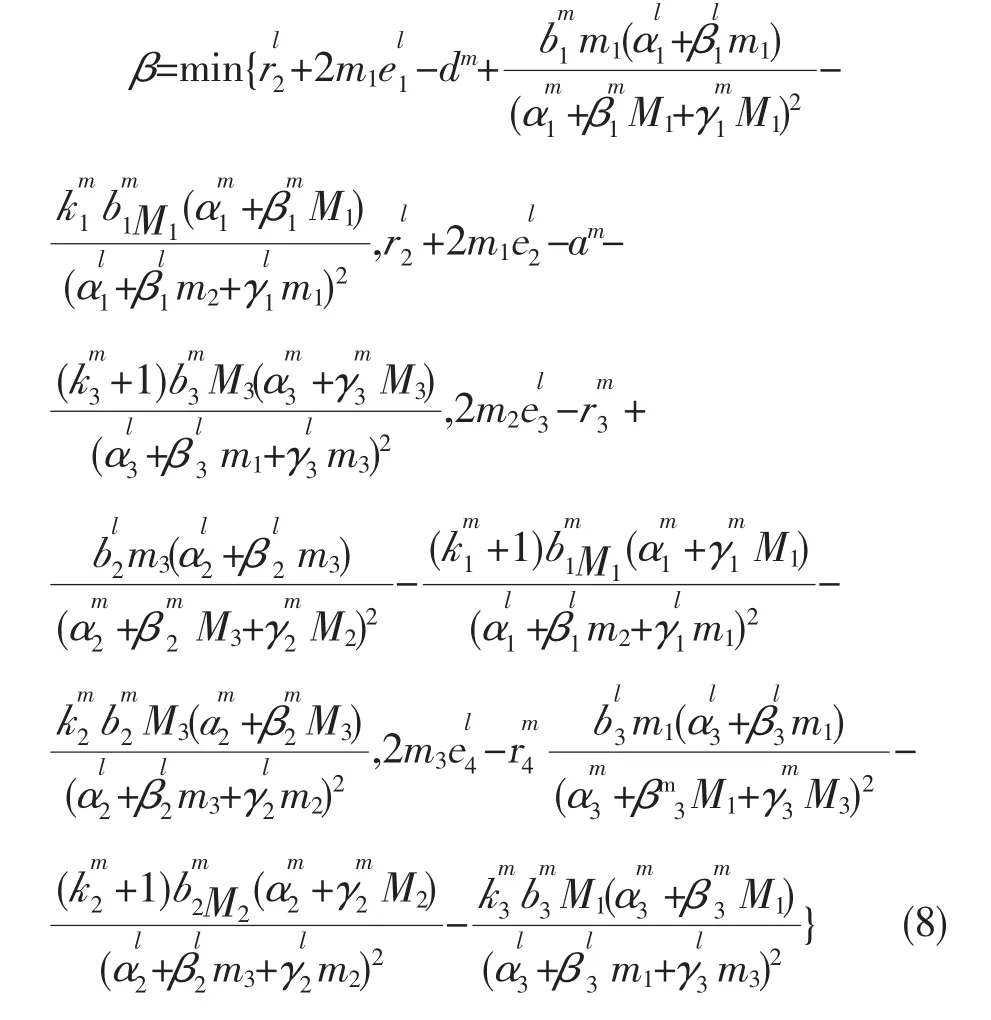
则t≥T。

对(8)两端从T到t积分得

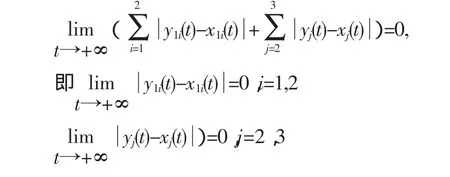
故系统(2)存在唯一全局渐近稳定的周期正解。

注释：

① 本文在文献[1]的基础上将阶段结构引入三种群顺环捕食系统中，使系统更接近实际的生态意义，同时又将文献[2]的研究推广到三种群顺环捕食系统使研究的难度进一步加大。

② 系统(1)所具有的生态意义是：当自然环境与人类对环境干预的共同作用下，具有阶段结构和Beddington-De Angelis功能性反应的三维顺环捕食生态系统在一定条件下，会出现周期平衡震荡，这对环境保护和生态平衡都具有一定的意义。

[1]李淑萍,靳 祯.具有Beddington-DeAngelis功能性反应的三维顺环捕食系统[J].中北大学学报:自然科学版,2008,29(3):195-200.

[2]Chen F D,You M S.Permance,extinction and periodic solution of the predator-prey system with Beddington-DeAngelis functional response and stage structure for prey[J].nonlinear Analysis:Real World Applications,2008,9:207-221.

[3]Song X Y,Chen L S.A predator-prey system with stage structure and harvesting for predator[J].Ann of Diff Eqs,2002,18(3):264-277.

[4]谢燕霞,魏凤英.一类具有阶段结构和HollingⅡ类功能反应的多种群捕食系统[J].福州大学学报:自然科学版,2010,38(1):1-5.

[5]刘会民,刘 兵.三种群竞争系统的持久性[J].生物数学学报,2001,16(1):46-53.

[6]姚志健.多种群阶段竞争系统的周期解与概周期解[J].生物数学学报,2008,23(1):116-124.

[7]陆忠华,陈兰荪.周期系数三种群Lotka-Volterra混合模型分析[J].纯粹数学与应用数学,1995,11(2):38-45.

[8]童姗姗,窦霁虹,贾 玲.基于实例的基因分类及确定基因标签模型[J].纯粹数学与应用数学,2011,27(4):515-522.

[9]马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996.

[10]晋金才,杨建飞.一类捕食者具有自食现象生态系统的周期解[J].商洛学院学报,2011,25(6):6-9.

[11]时 宝,张德存.微分方程理论及其应用[M].北京:国防工业出版社,2005.

[12]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2001.