尺寸和边界形貌对三角锯齿型石墨烯量子点的磁性影响

何彬，王卓，黄忠兵,2

(1.湖北大学物理学与电子技术学院，湖北 武汉 430062；2.北京计算科学研究中心，北京 100084)

0 引言

石墨烯是一种由碳原子以sp2杂化轨道构成的单层片状结构的新材料，自被发现以来，这一新材料引起了全世界的研究热潮.石墨烯以其独特的物理、化学和机械性能，在信息、能源以及器件制造等方面有巨大的应用前景[1-13].蜂巢状的晶体结构决定石墨烯具有2种高度对称的边界：扶手椅型(armchair)和锯齿型(zigzag).石墨烯层内的碳原子电子轨道产生sp2杂化，在石墨烯平面上形成σ键，在垂直石墨烯平面方向形成π键，且对整个石墨烯的性质起主要作用.为了消除边界上悬挂键对体系的影响，一般采用吸附氢原子的方法饱和边界上的悬挂键.研究表明，通过蚀刻等化学方法可以将石墨烯片分割成多种形貌的低维石墨烯纳米材料[1, 12]，具有代表性的结构包括石墨烯纳米带及石墨烯量子点.这些低维石墨烯结构在实验和理论研究中均被发现具有磁性[1, 2, 4, 13]，特别是三角锯齿型石墨烯量子点(TGQDs)，由于石墨烯层内2种亚点阵数目不同，从而导致体系内电子的总自旋不为零.

石墨烯量子点的磁性与其尺寸的大小、形状以及边界形貌等因素有密切的关系.在单层正三角锯齿型石墨烯量子点(ZZ)中，由于体系中2种亚点阵位置上碳原子的数目不同且其差值随尺寸的增加而增大，使得体系的自旋多重度S(S=2s+1，s表示量子点的总自旋)和总磁矩随着体系尺寸的增加而增大.总磁矩主要来源于锯齿型边界上碳原子的2p轨道上非键态π电子的贡献[1].为了理解边界形貌对三角锯齿型石墨烯量子点磁性的影响，Voznyy O等用五环和七环交替重新构建三角石墨烯量子点的边界(ZZ57)[2]，讨论氢化与不氢化2种情况下，结果表明ZZ和ZZ57具有相对稳定性，边界不氢化的ZZ57的能量最低，说明ZZ57的这种边界形貌可能存在.当边界重构后，除了尺寸很小的外，其他尺寸的基态均处于反铁磁态，说明边界重构对量子点的电子结构和磁性有很大影响.本文中结合约束路径量子蒙特卡罗(CPMC)计算方法和基于密度泛函理论的第一性原理计算方法，研究不同尺寸下2种不同边界的石墨烯量子点(ZZ和ZZ57)的磁学特性和电子结构特征.在量子蒙特卡罗计算中，将电子之间的关联效应作了严格处理，以便更为准确地反映相互作用π电子体系的内在物理特性.将2种方法的计算结果进行分析对比,可以全面地理解石墨烯量子点的磁学特征.

1 计算方法

在基于密度泛函理论的第一性原理的计算中，采用广义梯度近似(GGA)和电子交换关联函数PBE(Perdew-Burke-Ernzerhof)相结合的方法，计算采用的Dmol3软件包全电子波函数，精确描述碳原子轨道中的每个电子，并使用一个类3d的轨道波函数DNP基矢描述极化轨道，计算中使用的原子轨道截止半径是0.37 nm.在几何优化的过程中，力的收敛标准是0.02 Ha/nm(1 Ha=27.21 eV)，能量收敛标准是10-5Ha，最大位移收敛为0.000 5 nm,得到的石墨烯C—C键长为0.141 8 nm，与实验结果基本一致.为了正确描述石墨烯量子点的磁学特征，采用自旋非限制方法对所有可能的自旋多重度进行优化，选取能量最低的状态作为基态进行分析.

采用单轨道哈伯德模型描述石墨烯量子点中相互作用π电子的物理特性,该模型已被广泛用于研究含碳材料中由sp2轨道杂化而导致的磁性[5,10]，标准的哈伯德模型的形式为：

(1)

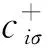
为了得到式(1)模型中的基态波函数|Ψ0〉，采用约束路径量子蒙特卡罗方法对一个已知的试探波函数|ΨT〉(通常选取为自由电子波函数并由单个slater行列式表示)投影得到[6,7]：

(2)

为了消除在约束路径量子蒙特卡罗方法中自由电子波函数的简并情况，用Hartree-Fock方法改写式(1)模型的哈密顿量，其形式为：

(3)

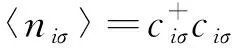
2 计算结果与讨论

图1 优化后的ZZ(a)和ZZ57(b)的几何结构示意图

为了研究不同尺度下边界对体系磁性和电子结构的影响，本文中计算了2种不同边界形貌、尺寸分别为4、6、8的三角锯齿型石墨烯量子点(TGQDs).用N表示TGQDs的尺寸，其值等于三角形任意一条边上碳环的个数.图1显示了N=6的规则边界三角锯齿型石墨烯量子点(ZZ)和不规则边界三角锯齿型石墨烯量子点(ZZ57)的几何结构示意图,边界上白色小球代表吸附的氢原子.ZZ中碳原子均以六环形式紧密排列在一起，量子点层内碳原子有2类不同的亚点阵位置A和B，图中白色球代表A，灰色球代表B.分别占据A和B位置的碳原子数目NA和NB是不同的，NA-NB=N-1.ZZ57中每个顶角都是七环-六环-五环的排列，3条边上均是以五环-七环交替构成新的边界，其中碳原子的数目与ZZ中碳原子数目相同，如图1(b)右边的ZZ57侧视图所示，这种结构的中间出现轻微的凸起.边界上吸附氢原子饱和悬挂键，量子点中碳原子的数目NC=N2+4N+1，边界吸附氢原子的数目NH=3N+1.

图2 N=6时ZZ57的自旋密度分布示意图 (a)约束路径量子蒙特卡罗计算方法的结果(b)DFT计算方法的结果

采用约束路径量子蒙特卡罗方法和Dmol3软件包计算了3种尺寸下量子点的自旋密度分布.以N=6的ZZ57的自旋电子密度为例，如图2所示，图2(a)描述的是采用约束路径量子蒙特卡罗计算方法得到的自旋密度分布示意图，图2(b)描述的是采用Dmol3软件包计算得到的自旋密度分布示意图.图2(a)和图2(b)中黑色的球代表自旋密度,即自旋向上的电子密度与自旋向下的电子密度的差值，球的大小正比于该格点上自旋密度分布的多少.从图中明显看出，自旋密度主要分布在量子点的边界上，量子点的中间部分只有很少的自旋密度分布，这与规则边界石墨烯量子点的自旋密度分布类似，采用2种方法得到的自旋密度分布的规律是相同的.

采用Dmol3软件包计算了3种尺寸的ZZ和ZZ57在不同自旋多重度下其体系的结合能，能量单位为Ha.如表1所示，表中加粗了的数值是不同尺寸下量子点基态时的结合能. ZZ均是在S=N时，能量最低，基态均处于铁磁态.在ZZ57中，N=4时，高自旋态能量最低，基态在此时还是处于铁磁态，N=6、8时，最低自旋态的能量最低，基态处于反铁磁态.当N=8时，ZZ构型的基态能量为-30.393 318 6 Ha，ZZ57构型的基态能量为-30.094 931 0 Ha.二者的平均结合能(结合能除以边界上的氢原子的数目)刚好相差0.3 eV，这与文献[2]中得到的结果一致，验证了计算中所取参数的可靠性.

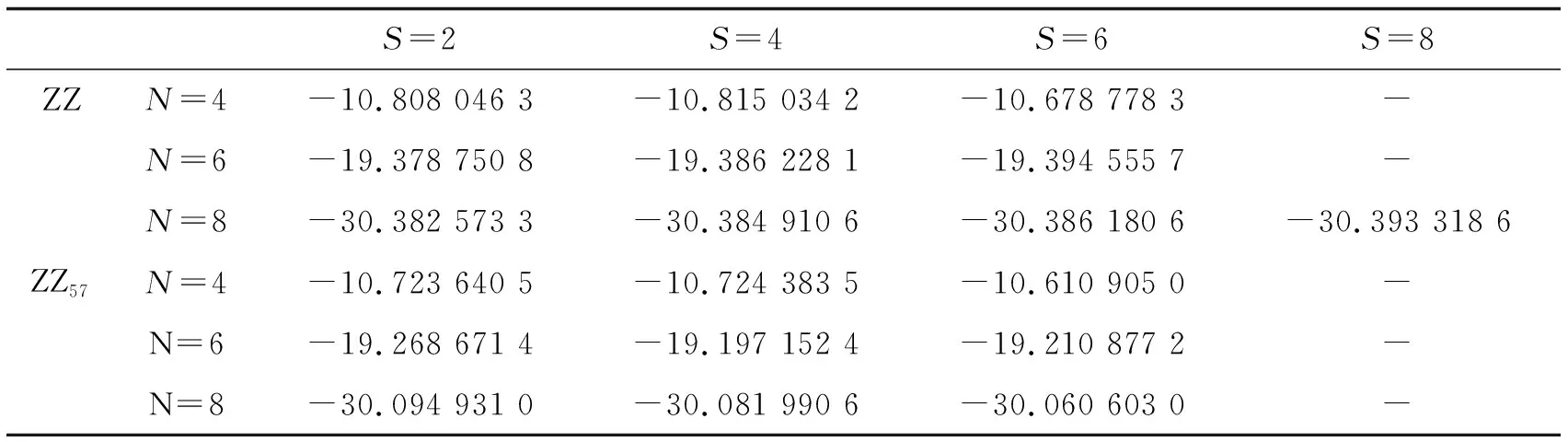
表1 3种尺寸的石墨烯量子点在不同自旋多重度下体系的结合能

为了确认采用Dmol3软件包得到的结果的正确性，采用约束路径量子蒙特卡罗方法计算了3种尺寸的ZZ和ZZ57在各个自旋多重度下其体系的能量，在计算中取U/|t|从0变化到3.0,如图3所示，图3(a)中ΔE表示ZZ在S=N-2与S=N时，体系能量的差值，图3(b)中ΔE表示ZZ在S=N+2与S=N时，体系能量的差值,图3(a)和图3(b)中ΔE始终大于零.3种尺寸的ZZ，体系均是在S=N时能量最低，基态均处于铁磁态.该结果与Dmol3软件包及其他第一性原理计算的结果一致.图3(c)中ΔE表示的是3种尺寸的ZZ57在S=2与S=4时，其体系能量的差值.N=4时，ΔE始终大于零，高自旋态时能量最低，基态在此时仍然处于铁磁态.随着尺寸的增大，N=6、8时，ΔE始终小于零，最低自旋态时能量最低，量子点的基态处于反铁磁态.边界重构使三角锯齿型石墨烯量子点从铁磁态转变为反铁磁态.

图3 3种尺寸下ZZ和ZZ57不同自旋多重度下其能量的差值

图4 ZZ(a)和ZZ57(b)(N=4)的自旋向上和自旋向下电子态密度图虚线表示费米能级EF

体系的磁性一般认为是由费米面附近的上下自旋电子极化所导致，采用Dmol3软件包计算量子点费米面附近的上下自旋电子态密度分布.如图4所示，虚线表示体系的费米能级EF，图4(a)和图4(b)分别描述在尺寸N=4时，ZZ和ZZ57的自旋向上和自旋向下的电子态密度分布，其中0点以上的曲线代表自旋向上的电子态密度，0点以下的曲线代表自旋向下的电子态密度.ZZ在费米能级附近出现明显的自旋劈裂，即在EF处自旋向上态密度处于峰值，而自旋向下的态密度分布基本为零，导致较强的自旋极化.而边界重构后在费米能级附近虽然还存在自旋劈裂，但是此时自旋向下的态密度明显不为零，极化程度在一定程度上已经被削弱.在N=6、8时，ZZ57在费米能级附近已经不存在明显的自旋劈裂.

3 结论

利用约束路径量子蒙特卡罗计算方法和基于密度泛函理论的第一性原理计算方法研究了不同尺寸的ZZ和ZZ57的磁学特性和电子结构特征，结果表明：ZZ在所有尺寸下均为在较高自旋态时，能量最低，量子点基态处于铁磁状态，且磁矩的大小随着ZZ的尺寸增大而增大；ZZ57在N=4时，体系仍是高自旋态能量最低，而在N=6、8时，基态均处于最低自旋态，量子点处于反铁磁状态.在费米能级附近，ZZ出现了明显的自旋向上和自旋向下态密度分布的劈裂，ZZ57除了N=4以外，费米能级附近没有出现自旋的劈裂.不规则边界对量子点的自旋极化有阻碍作用，边界重构使三角锯齿石墨烯量子点从铁磁状态转变为反铁磁状态.2种方法得到的计算结果相互肯定，为真正实现该类材料的磁性可控打下了了基础.

致谢：感谢湖北大学物理学与电子技术学院同课题组的杨敏、刘光坤的交流讨论.

[1] 潘洪哲，徐明，陈丽,等.单层正三角锯齿型石墨烯量子点的电子结构和磁性[J].物理学报，2010,59:6443-6449.

[2] Voznyy O. Effect edge reconstruction and passivation on zero-energy states and magnetism in triangular grapheme quantum dots with zigzag edges[J]. Phys Rev B, 2011,83(16): 165417(1)-(5).

[3] Potasz P. Zero-energy states in triangular and trapezoidal grapheme structures[J]. Phys Rev B, 2010,81:033403-033406.

[4] Güçlü A D, Potasz P, Hawrylak P. Electric-field controlled spin in bilayer triangular grapheme quantum dots[J]. Phys Rev B, 2011,84:035425-035429.

[5] Oleg V Y.Emergence of magnetism in grapheme materials and nanostructures[J]. Rep Prog Phys, 2010,73:056501(1)-(16).

[6] Huang Z B, Lin H Q. Quantum Monte Carlo study of spin, charge and pairing correlations in the t-tˊ-U Hubbard model[J]. Phys Rev B, 2001,64:205101(1)-(6).

[7] Zhang Shiwei. Constrained path Monte Carlo method for fermion ground states[J]. Phys Rev B, 1997,55(12):7464-7477.

[8] Bahamon D A. Inner and outer edge states in grapheme rings: a numerical investigation[J]. Phys Rev B, 2009,79:125414-125421.

[9] Fernandez-Rossier J, Palacios J J. Magnetism in grapheme nano-islands[J]. Phys Rev Lett, 2007,99:177204-177207.

[10] Soriano D, Muoz-Rojas F. Hydrogenated graphene nanoribbons for spintronics[J]. Phys Rev B, 2010,81:165409(1)-(4).

[11] Oleg V Y, Katsnelson M I. Magnetism and correlations in fractionally filled degenerates shells of graphene quantum dots[J]. Phys Rev Lett, 2009,103(24):246805(1)-(4).

[12] Ci Lijie, Xu Zhiping. Controlled nanocutting of graphene[J]. Nano Res, 2008,1:116-122.

[13] Potasz P. Electronic and magnetic properties of triangular grapheme quantum rings[J]. Phys Rev B, 2011,83:174441(1)-(6).