非强占优先权模型中高优先权顾客队长平稳分布的概率母函数

潘全如

(江苏科技大学 数理学院,江苏 镇江 212003)

单一的服务标准往往无法满足某些业务的要求,这就需要把顾客划分成不同的优先等级,按照优先级确定其获得服务的次序与质量.目前具有优先权的模型已获得了广泛应用[1-2],且已取得了较好的结果[3-4]，但大多数都是基于服务时间服从指数分布[5-6].文中就非强占服务规则建立了服务时间服从一般分布且有优先权的排队模型.

1 模型假设

1)顾客包含i个顾客类,每一类均以泊松流到达系统,第i类顾客的到达率为λi(i=1,2),不同类型的顾客到达过程独立.

2)相同优先级的顾客先到先服务;不同优先级的顾客根据优先级确定服务的先后顺序.设第1类顾客的优先级高于第2类顾客的优先级.

3)系统中只有一个服务窗口,容量无限.

4)系统为每一类顾客服务的时间服从一般分布,且第i类顾客的服务时间分布记为Bi(x),规定不同类型的顾客服务过程独立.

5)若高优先权顾客到达系统时,低优先权顾客正在进行服务,服务台并不中断现有的服务.此高优先权的顾客一直等到正被服务的低优先权顾客服务完毕,才开始接受服务.

2 模型分析

假定λ1β1+λ2β2<1及系统平稳分布存在.令qn(i)分别为在第n次离开系统后的瞬间,系统中第i(i=1,2)类顾客的队长.记qn(1)的平稳分布的母函数为

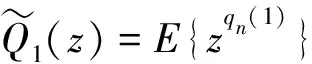
(1)

P0为顾客第n次离开后瞬间系统中没有顾客的概率,易知

P0=1-λ1β1-λ2β2

(2)

再令

(3)

定理在非强占优先权下,第1类顾客离开系统后的瞬间,第1类顾客的队长平稳分布的概率母函数记为Q1(z),则

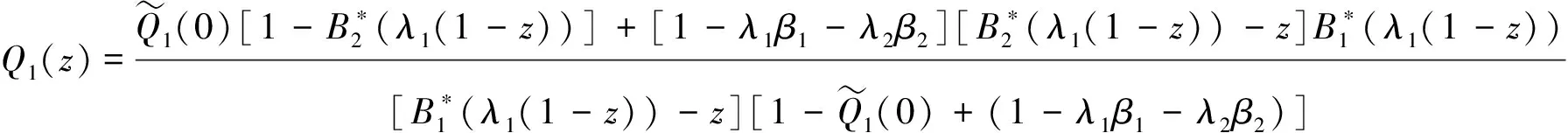
(4)

其中

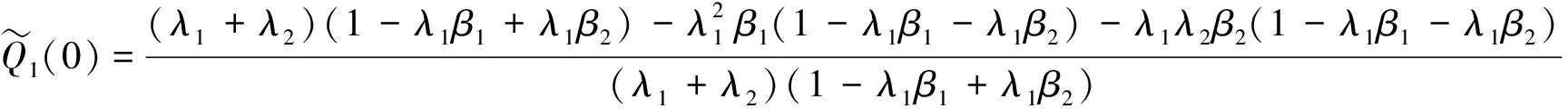
(5)

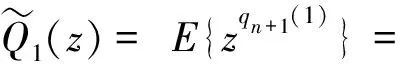
E{zqn+1(1)|qn(1)>0}P{qn(1)>0}+

E{zqn+1(1)|qn(1)=0,qn(2)=0}P{qn(1)=0,

qn(2)=0}+E{zqn+1(1)|qn(1)=0,

qn(2)>0}P{qn(1)=0,qn(2)>0}

(6)

记E1=E{zqn+1(1)|qn(1)>0}P{qn(1)>0}

E2=E{zqn+1(1)|qn(1)=0,qn(2)=0}P{qn(1)=0,qn(2)=0}

E3=E{zqn+1(1)|qn(1)=0,qn(2)>0}P{qn(1)=0,qn(2)>0}

在E1中,当qn(1)>0时,qn+1(1)=qn(1)-1+vn+1(1),其中vn+1(1)是在一个第1类顾客的服务时间中到达的第1类顾客的数目,其概率母函数为

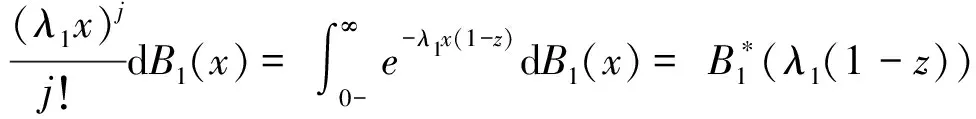
(7)

所以E1=E{zqn(1)-1+vn+1(1)|qn(1)>0}·

P{qn(1)>0}=E{zqn(1)|qn(1)>

0}z-1E{zvn+1(1)}P{qn(1)>0}=

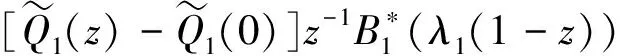
(8)

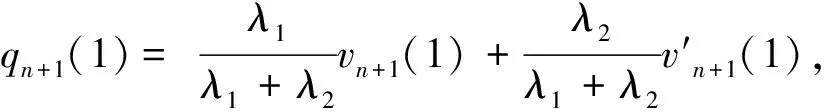
E2=P0E{zqn+1(1)|qn(1)=0,qn(2)=0}=

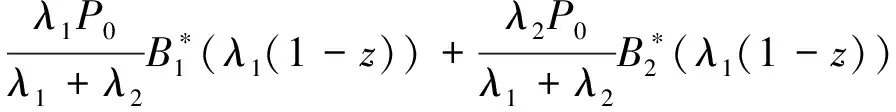
(9)

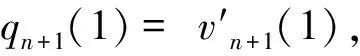
(10)

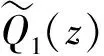
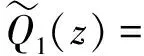
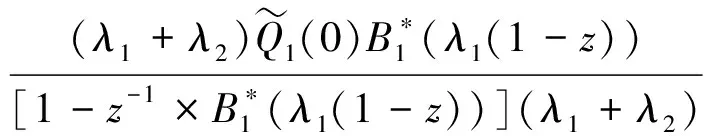
(11)

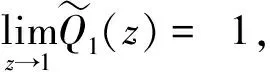
令G1(z)=P{xn+1=1}E{zqn+1(1)|xn+1=1}

(12)

则G1(z)=E{zqn+1(1)}-P{xn+1=0}·

P{qn(1)=0,qn(2)>0}E{zqn+1(1)|qn(1)=0,qn(2)>0},将E3代入得:

将(11)代入(13)得:

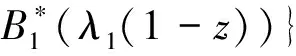
(14)

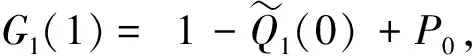
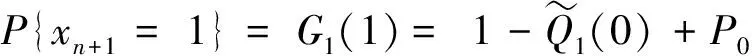
(15)

于是由Q1(z)的定义及式(12)得:

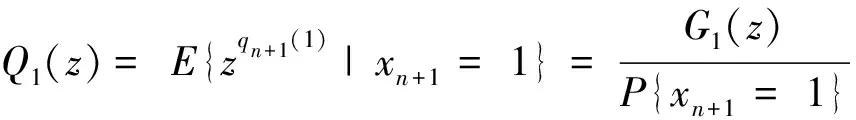
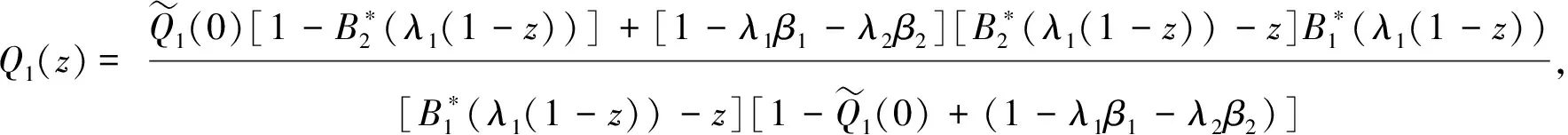
3 结论

优先权排队理论具有重要的应用价值,文中对非强占优先一类特殊M/G/1模型中高优先权顾客队长概率母函数作了定量分析.关于优先权理论还有很多值得进一步研究的问题,比如系统的利用率[7-8]、顾客类多于两个的情况等等.

[1] 朱广萍.优先权排队问题的分析[J].西南民族大学学报:自然科学版,2004,30(2):134-137.

Zhu Guangping.An analysis of the queuing system of priority[J].JournalofSouthwestUniversityforNationalities:NaturalScienceEdition,2004,30(2):134-137.(in Chinese)

[2] 戴琳,秦叔明,张卫锋.普通顾客排队且排队顾客优先的混合排队问题[J].工程数学学报,2012,29(5):689-695.

Dai Lin,Qin Shuming,Zhang Weifeng. A mixed queueing problem with common customers queue and the queueing priority[J].ChineseJournalofEngineeringMathematics,2012,29(5):689-695. (in Chinese)

[3] 刘建民.高负荷下带重尾服务强占优先排队的扩散逼近[J].纯粹数学与应用数学,2010,26(4):559-566.

Liu Jianming. A heavy traffic diffiusion approximation for preemptive resume priority queueing with heavy tailed service[J].PureandAppliedMathematics,2010,26(4):559-566. (in Chinese)

[4] 徐祖润,李敏捷,朱翼隽,等.带负顾客和强占优先权的不耐烦信元排队[J]. 数学的实践与认识,2010,40(23):142-148.

Xu Zurun,Li Minjie,Zhu Yijun,et al. Impatient cells’ queueing with negative customers and preemptive priority[J].MathematicsinPracticeandTheory,2010,40(23):142-148. (in Chinese)

[5] 徐祖润,李敏捷,潘全如.带有负顾客的M/M/c 单重工作休假排队[J]. 江苏科技大学学报:自然科学版,2011,25(5):500-504.

Xu Zurun,Li Minjie,Pan Quanru. M/M/c queue with negative customers and single working vacation[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2011,25(5):500-504. (in Chinese)

[6] 潘全如,朱翼隽,陈佩树.有反馈和N-策略多重休假的M～X(G,G-m)/1排队模型[J].江苏科技大学学报:自然科学版,2007,21(5):80-85.

Pan Quanru,Zhu Yijun,Chen Peishu. An M～X/(G,G-m)/1 queue model with N-policy,multiple vacation and feedback[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2007,21(5):80-85. (in Chinese)

[7] Pan Quanru.Low priority customer behavior analysis of an M/G/1 model with nonpreemptive priority[J].MathematicaAeterna,2013,3(3): 201-204.

[8] 谢锦山,陈德南.仓库容量有限条件下的离散型随机存贮管理策略[J].龙岩学院学报,2010,28(5):15-18.

Xie Jinshan,Chen Denan. Discrete random storage strategy under condition of limited storage capacity[J].JournalofLongyanUniversity,2010,28(5):15-18. (in Chinese)