应力状态对饱和重塑粘性土强度影响的CU试验研究

梅 岭, 周爱兆, 姜朋明

(江苏科技大学 土木工程与建筑学院, 江苏 镇江 212003)

图1 条形均布荷载下地基内任一点受力Fig.1 Stress of soil point under the strip footing

而实际上,土层在其沉积历史过程中形成的各向异性使得M点上土的自重应力在各个方向是不相等的,即静止土压力系数K0≠1,因此在M点产生的附加大、小主应力方向和自重应力方向并不一致,所以这两项应力不可以简单相互叠加．假设K0=1时,也即假设土体处于球应力的状态下,从而使土体人为地处于更加密实的状态,所得临塑荷载和临界荷载必然偏大,得到的地基承载力是偏不安全的,文献[3-6]的研究都证明了这一点．

为此,设计不同K0初始应力状态下的CU试验,来研究地基土不同应力状态对其强度的影响,以及假设K0=1对强度造成的误差．

1 试验研究

1.1 试验仪器

试验采用英国产GDS多功能三轴仪．该设备吸取了当今先进的机械制造工艺和自动控制技术,测量、控制精度高且实现了数字化操作．与传统三轴仪一样,GDS三轴仪主要也是由压力室、轴向加压设备、围压施加系统、体积变化和孔隙压力量测系统所构成．不同的是GDS中增加了计算机控制与分析系统,与传统三轴仪相比,试验结果具有更好的精度与可操作性．

1.2 试验方案

试验采用南京江北某基坑粉质粘土,其常规物理力学性质指标如表1．

表1 土的物理性质指标Table 1 Basic physical properties of the soil

令饱和重塑粘性土在不同K0应力状态下固结,进行4组固定围压,施加轴向压力直至土样破坏的固结不排水试验．具体试验设计方案见表2．

表2 试验方案Table 2 Experimental plan

1.3 试验步骤

1.3.1 排出气体

首先开启GDS系统,选用Saturation Ramp试验模块,设置较小的围压及反压,用来排除试样与橡皮膜之间的空气,持续大约30 min．

1.3.2 试样饱和

选用Saturation Ramp试验模块,重新设置围压及反压,进行试样饱和,时间持续为10～15 h．

1.3.3 孔压系数B测定

选用B-Check模块,保持反压不变,增加围压,根据孔压变化值计算孔压系数B,若B值达0.98以上可视土样为饱和．否则将重新进行饱和．

1.3.4 固结

1.3.5 剪切

在固结完成的基础上,选用Advance loading试验模块,反压仍然保持不变,在不同的固定围压下,施加轴向压力至土样破坏,加载速率为0.04 mm/min．

1.3.6 卸样

将所有压力回零,待排去压力室中水后,拆去压力室外罩,脱去试样外橡皮膜,将仪器擦洗干净．

2 试验结果

2.1 围压对土体强度的影响

图2a)和b)是试样在K0分别为0.5及1.0初始固结作用后,不同围压作用下逐步施加轴向应力直至土样破坏的偏应力与轴向应变的关系．

由图可知,当土样在某一K0条件下固结后,随着偏应力的增加,试样的轴向变形ε1逐渐增大;随着围压的增大,土样达到相同的轴向应变时所需的偏应力逐渐增大,土样的破坏应力也逐渐加大．此即说明越是深层的土体,由于其所受围压越大,则其达到破坏所需的荷载就会越大．而且,土样在某一轴向应变时,增加相同幅度的围压,所需的偏应力的增量逐渐减小,也即当土层达到一定深度以后,其承载性能趋向于稳定．所以,初始围压对土体破坏时主应力强度有影响,其值随着围压值的增加而增加．当初始围压越小时,加载时土样越容易破坏．其他K0下也有类似规律,这里不再赘述．

a) K0=0.5

b) K0=1.0

2.2 K0对土体强度的影响

图3a)和b)是σ3分别为100和200 kPa时不同K0下偏应力与轴向应力之间的关系．由图3可以看出,在某一围压下,随着固结应力比K0从0.5增大到1.0,土样的应力～应变关系曲线初始坡度逐渐由缓变陡．随着K0的增大,试样达到破坏时需要的偏应力也越大,即需要施加的轴向压力越大．围压一定时,要达到同一轴向应变,K0越大,所需的偏应力就越大．这说明,在基底以下某一深度的土体,此时有着相同的围压,要达到同一的竖向位移,K0越大的土体,所需的竖向力就越大,从而土体达到破坏时的竖向力就越大,即其承载力越高．假设土体的K0=1,高估了土体的承载能力,造成不安全的结果，再次验证了文献[7]提出的Terzaghi承载力理论常常过高地估计浅基础的承载能力的观点．

从图3还可以了解到,某一围压下,在同一偏应力作用时,K0越大,土体的轴向应变就越小．也即说明相同深度的地基土在同一竖向力的作用下,静止土压力系数越大的土体,其竖向变形就越小．假设土体的K0=1,则理论上其沉降量应该较小,而实测沉降量要越大于理论值,这正是K0=1这一不合理假设所导致的[8]．目前有些地区的工程中,用临界荷载承载力公式确定的地基承载力特征值远大于按变形确定的承载力特征值,也正说明了这一点．其他围压时,不同K0下偏应力与轴向应力之间的关系也有类似规律,这里不再赘述．

a) σ3=100 kPa

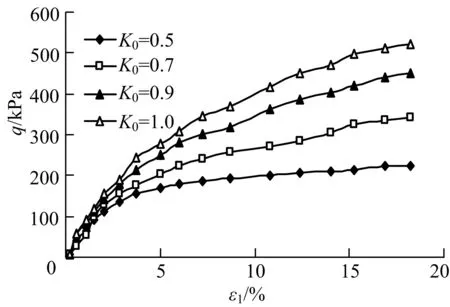
b) σ3=200 kPa

2.3 破坏偏应力的变化率

为研究各围压下,不同K0时土样轴向加载的破坏点的差异,现做如下分析．

《土工试验方法标准(GBT50123-1999)》第16.5.14中规定[9]:以主应力差或有效主应力比的峰值作为破坏点,无峰值时,以有效应力路径的密集点或轴向应变15%时的主应力差值作为破坏点．则对各围压下,不同K0时土样在轴向加载情况下得到的应力～应变曲线进行拟合,在拟合方程中取轴向应变ε1=15%,计算得到此时的偏应力q,并在不同围压下,假设K0=1时土样的破坏偏应力为1,则各K0值时偏应力的变化率详见表3．

表3 土样在不同围压及K0条件下破坏偏应力的变化率Table 3 Variation rate of failure deviator stress in different conditions

由表3可以看出,在某一围压下,随着K0从1.0变化到0.9，0.7及0.5时,土样的破坏偏应力分别下降了20%，35%以及55%左右,不同围压下均有类似规律．虽然不能用土样的破坏应力来代替地基土的破坏荷载,但这一现象在一定程度上也能说明若地基土的实际侧压力系数为0.5，0.7或0.9,而按照规范或教材中假设K0=1的方法来求其承载能力,则其结果可能会分别被高估55%，35%及20%．

3 结论

通过4组不同K0状态下饱和重塑粘性土的CU试验,得到了相应偏应力与轴向应变的关系,指出了假设土体K0=1的错误,研究了地基土不同应力状态对其强度的影响,得到了假设K0=1对土体强度造成的误差,主要结论如下:

1) 初始围压对土体破坏时主应力强度有影响,其值随着围压值的增加而增加,初始围压越小,土样越容易破坏;

2) 土体固结应力比K0对土体破坏时的主应力强度有较大影响,其值随着K0的增加而增加,固结应力比K0越小,土样越容易破坏;

3)假设土体的K0=1,高估了土体的承载能力,造成不安全的结果,土体实际的K0越小,误差越大．

参考文献(References)

[1] Craig R F.Craig′s soil mechanics[M].[S.l.]: VNR International, Molly Millars Lane, 1995: 296-299.

[2] 中华人民共和国建设部，国家质量监督检验检疫总局.GB50007-2002 建筑地基基础设计规范[S].北京: 中国建筑工业出版社, 2002.

[3] 赵树德.地基弹塑性承载力K0≠1时的计算公式[J].西安建筑科技大学学报, 1995, 27(3): 294-298.

Zhao Shude.Formulation of bearing capacity of subgrade withK0≠1 [J].JournalofXi′anUniversityofArchitecture&Technology, 1995, 27(3): 294-298.(in Chinese)

[4] 崔江余, 宋金峰.地基临塑荷载的分析[J].工程力学, 1998, 15(4): 96-100.

Cui Jiangyu, Song Jinfeng.The analysis of the critical edge pressure for subsoil [J].EngineeringMechanics, 1998, 15(4): 96-100.(in Chinese)

[5] 董江平, 张雄壮, 洪雷, 等.超软海底淤泥吹填地基无砂垫层真空预压处理效果研究[J].江苏科技大学学报:自然科学版, 2010, 24(4): 335-340.

Dong Jiangping, Zhang Xiongzhuang, Hong Lei, et al.Effect of no-sand cushion vacuum preloading on ultra-soft seabed silt hydraulic fill foundation [J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition, 2010, 24(4): 335-340.(in Chinese)

[6] 许英, 徐骏, 吴兴祥.港口工程大直径管桩竖向承载力可靠性研究[J].江苏科技大学学报:自然科学版, 2011, 25(6): 517-519.

Xu Ying, Xu Jun, Wu Xingxiang.Reliability study on vertical capacity of large-diameter cylinder pile in port engineering[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition, 2011, 25(6): 517-519.(in Chinese)

[7] Poulos H G, Davis E H.岩土力学弹性解[M].孙幼兰，译.北京: 中国矿业大学出版社, 1990: 43-44.

[8] 张坤勇, 殷宗泽.应力各向异性对地基变形的影响[J].岩土工程技术, 2004, 18(4): 180-183.

Zhang Kunyong, Yin Zongze.Influence on soil′s deformation with consideration of stress induced anisotropy[J].GeotechnicalEngineeringTechnique, 2004, 18(4): 180-183.(in Chinese)

[9] 中华人民共和国水利部.GBT50123-1999 土工试验方法标准[S].北京: 中国计划出版社, 1999.