一种基于改进型KNN算法的文本分类方法

钱 强， 庞林斌， 高 尚

(江苏科技大学 计算机科学与工程学院，江苏 镇江 212003)

随着Internet及其相关技术的飞速发展,互联网上出现了海量而庞杂的Web信息资源.如何从这些海量的非结构数据中提取和产生知识,找到人们感兴趣的内容,已经成为当前迫切需要解决的重要问题.中文文本分类技术作为解决这一问题的关键技术之一,日益成为研究的热点.其在搜索引擎、信息推送、信息过滤和自动问答等领域得到了越来越广泛应用[1].目前主流的文本分类算法有向量距离分类算法、朴素贝叶斯分类算法(NB)、K近邻分类算法(KNN)和支持向量机分类算法(SVM)等.其中KNN算法因为具有实现简单、无训练过程及较高的精度性能等优点,得到了广泛应用.但是KNN算法在实际应用过程中依然有一些不足之处,文中针对KNN算法的一些缺点提出相应的改进措施.

1 传统KNN算法

在模式识别领域中,KNN算法(最K近邻算法)是将特征空间中最接近的训练样本进行分类的方法.其中1NN算法(即最近邻算法)是最小距离分类算法的一种极端的情况,以全部训练样本作为代表点,计算测试样本与所有样本的距离,并以最近邻者的类别作为决策.

最初的近邻法是由Cover和Hart于1968年提出的[2],随后得到理论上的深入分析与研究,是非参数法中最重要的方法之一.KNN算法本质上是一种基于监督的实例学习的机器学习方法.在目前的主流分类算法中,KNN算法是比较适合在文本分类这一领域应用的.

KNN算法在所有的机器学习算法中比较简单被分配的对象被列为其邻域对象类别较多的分类的K近邻算法是最常见的(K是一个正整数,通常很小).如果K=1,那么对象被简单分配给其近邻的类.

KNN算法描述如下:

目标:分类未知类别案例.

输入:待分类的未知类别文本d.已知类别的文本集合D,其中包含M个已知的文本类别.

输出:文本d可能的类别.

步骤:

1)依式(1)计算新文本d与训练集中的所有文本d1,d2,…,dn之间的相似度.得到SIM(d,d1),SIM(d,d2),…,SIM(d,dn).

2)将SIM(d,d1),SIM(d,d2),…,SIM (d,dn)进行排序,若是超过相似度阈值t，则放入近邻文本集合NN.

3)自近邻文本集合NN中取出前K名,按照类别多数判决,从而决定新文本d的所属类别.

KNN算法中文本样本之间的相似度计算方法一般如式(1)所示:

SIM(di,dj)=cos(di,dj)=

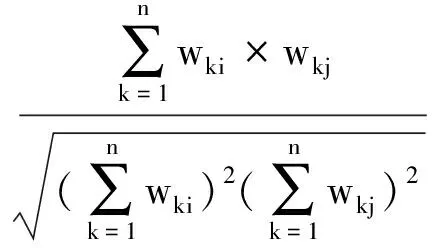
(1)

式中：di表示文本i所对应的特征向量;dj表示文本j所对应的特征向量;wki表示文本i的特征向量的第k维特征的特征值(权重);wkj表示文本j的特征向量的第k维特征的特征值(权重)[3].

通过对KNN算法的分析,可以知道该分类算法的优点主要有:首先，思路简单,实现容易;其次，当向训练样本集中加入新的文本时,不需要重新训练.但在KNN算法拥有上述优点的同时,也存在着一些不足的情况[4],比如:待分类文本类别是根据选出的K篇文本来确定的,所以对K值的选取将会影响分类的效果,但是目前只能通过不断的实验来调整K的取值,无法获取一个通用的K值参数;另外KNN算法的一个显著缺点是其计算复杂度高,对待分类文本进行分类时需要计算训练集中的所有样本到该文本的距离,从中排序选取前K个文本来决定文本类别.这样的话,无论是计算文本间距离所用的时间,还是训练集中样本存储的空间,都会随着训练集规模的变大和文本特征维数的增加而线性增加,其时间复杂度可以用O(m*n)来表示.其中,m是选出的特征项的个数,n是训练集中文本的个数.当分类模型的训练集规模比较大时,KNN算法的时间消耗也非常大.这大大限制了该算法的实际应用效果.

2 改进型的KNN算法

针对KNN算法在分类阶段计算复杂度大,耗时长的缺点,文中提出一种改进型的KNN算法,主要的思想是通过改进待分类文本的近邻点的查找策略,从而提高KNN算法的运行效率,降低其算法复杂度.

该算法的主要思想如下：首先计算出训练集中两两向量之间的距离；然后对这些距离进行比较排序,针对每一个训练向量,设计一种独特的数据结构形式,在其中存储了到该向量距离最短的前K个向量的集合和其他一些信息.以上为本算法的训练阶段.在分类阶段中,对于新到的待分类的测试向量,在训练集中随机性的找出一个训练向量,计算出该向量以及在其数据结构中离该向量距离最短的K个向量(共计K+1个向量)到待分类向量的距离.比较排序后找出到待分类向量距离最短的向量.再以此向量为基点,计算出该向量以及在其数据结构中离该向量距离最短的K个向量(共计K+1个向量)到测试向量的距离.如果是已经计算过距离的向量,则不做第2次计算.迭代此过程,一直找到距离测试向量的距离最短的前K个向量.再按照传统的KNN算法,计算出待分类的测试向量的所属类别.图1中显示了上述思想.

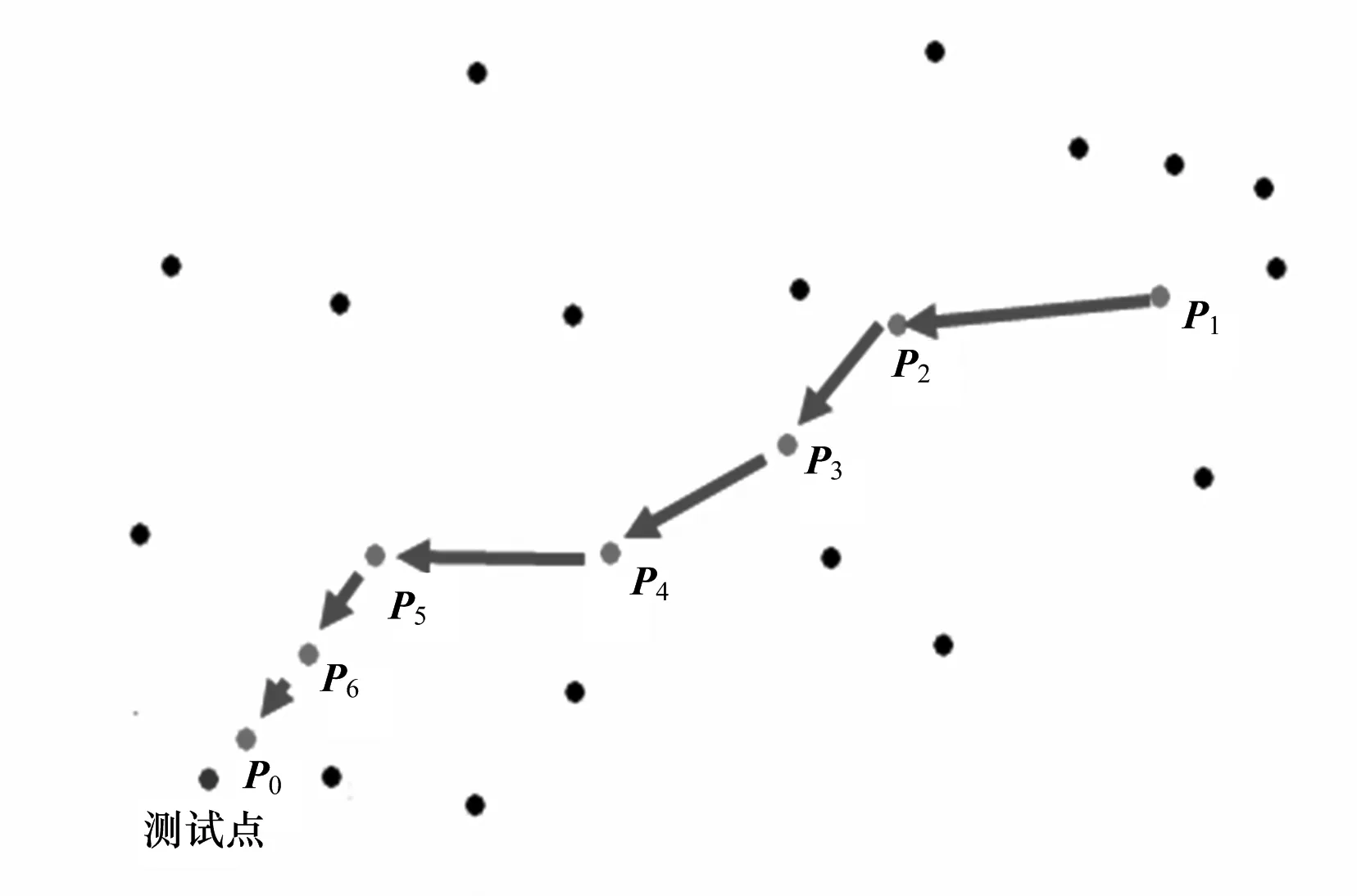
图1 通过搜索选择最近邻点Fig. 1 Select the nearest neighbor points through searching

在图1中,对于新到的待分类的测试向量,随机性的找出某训练向量,记为p1.按照前面讨论的方法,可以依次递归的找出p2,p3,…,pn向量.如果以K=3记,可以在pn向量的附近找出距测试向量最近邻的3个点.然后按照传统KNN算法的流程计算出待分类向量所属的类别.

在上面的算法中,可以看出由于改进了查找最近邻点的搜索策略,算法的计算复杂度将会大大降低,有很多明显对最终分类不起作用的向量将不会参与计算.但是也可能会出现一些问题,这主要是由最初随机查找初始向量的位置所带来的.如图2,如果一开始的随机向量被定为p1,那么最终迭代出离测试点距离最近的向量为p3.如果按照这样的方式计算,那么原本属于类别2的待分类向量则将会被错误的划分到类别1.另外该算法还可能出现的问题是,在本算法的查找过程中,由于搜索路径具有明显的方向性.这样,某些向量可能离最终的待分类向量更近,但是因为其不在搜索路径上,而没有参与最终的计算,从而造成了测试向量的分类错误.

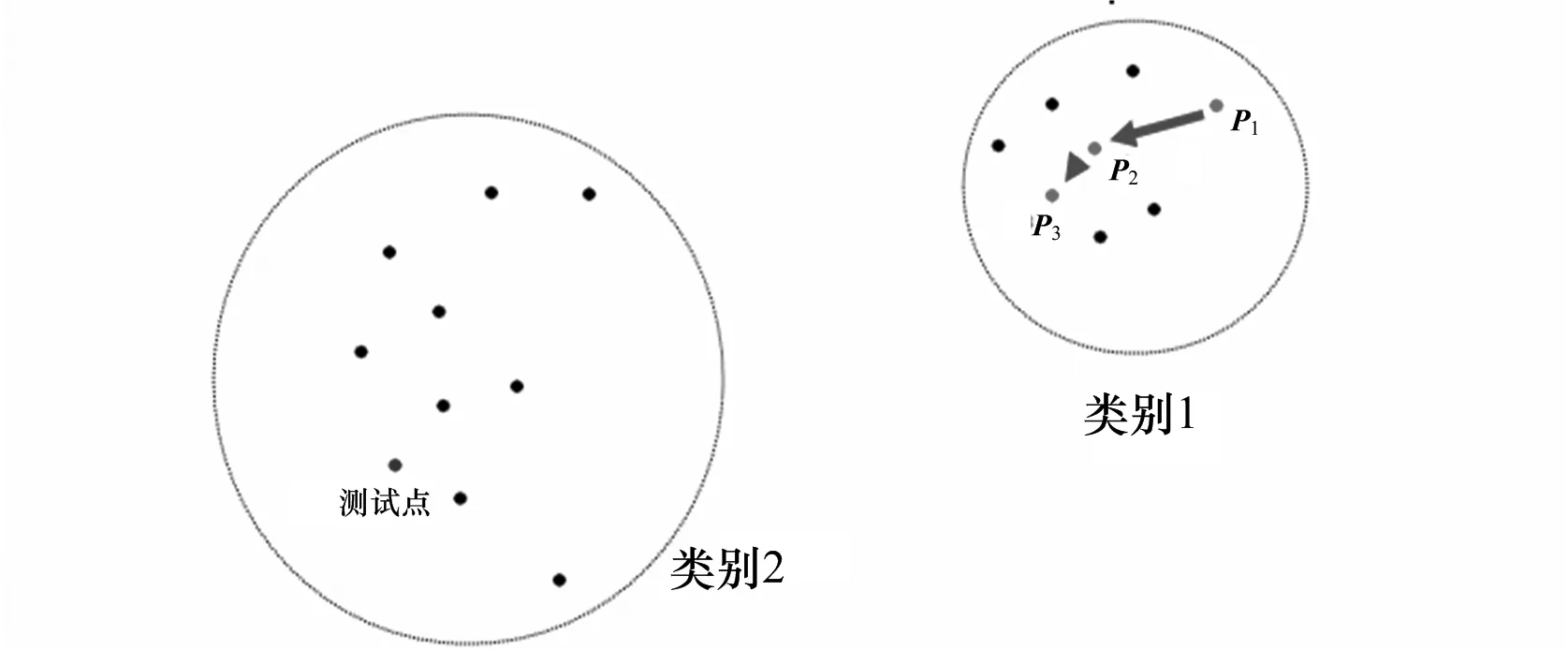
图2 错误的分类结果Fig. 2 Error classification results

对开始的初始化向量的定位方式做出改进,主要是利用了基于距离向量的算法思想.改进的方法如下:首先在样本的训练阶段，找出各个类别的中心向量，并对该中心向量也找出离其距离最近的K个训练样本(即将该中心向量也作为训练集的样本之一).这样,对于新到的待分类测试向量,首先以M个各类别的中心向量为初始化向量,然后以这些向量为起点分别作迭代.在迭代的计算过程中,对已经计算过的训练样本向量做出标记,以减少重复计算,或者直接在该向量的数据结构中记录其距测试向量的距离,直至最终找出距离待分类向量最近的K个向量,再按照传统的KNN算法来计算测试向量的所属类别.

基于这一改进思想,为了算法实现方便,对于训练集中的每个文本向量的表示设计了一种特殊的数据结构,其形式如表1.基于如表1中的数据结构,对该改进的KNN算法的算法步骤整理描述如下:

表1 训练集中的文本表示Table 1 Text representation for the training set

算法:改进的KNN算法

输入:训练文本集D={d1,d2,…,d|D|},属于类别集C={c1,c2,…,cM},K值,阈值T,待分类的测试文本d.

输出:d所属类别Cd.

步骤:

1)对训练集中的各个类，计算出其类别中心dc1,dc2,…,dcM;并进行训练集文本的初始化工作;

2)对训练集D中的每个文本di(包括类别中心dc1,dc2,…,dcM,计算其文本表示的数据结构.在训练集D中,计算出每一个文本到di的距离值,如果该值大于阈值T,则直接丢弃,如果该值小于T则予以保留;对计算出的所有距离进行排序,找出最小的K个距离所对应的文本,将这些文本写入di对应的数据结构的NearestNeighbors属性中.此为本算法的训练阶段;

3)对于新到的待分类的测试文本d,首先以c1类的类别中心文本dc1为基点,从dc1的NearestNeighbors属性中找出距离其最近的K个文本集合.计算出这些文本与待分类文本d的距离，并填入这些文本结构各自的Distance属性中.然后根据该属性,在这K+1个文本(dc1和距离它最近的K个文本)中找出距离待分类文本最近的新基点dn;

4)如果新基点dn就是c1类的类别中心文本dc1，则直接转入步骤7);

5)从dn的NearestNeighbors属性中找出距离其最近的K个文本集合.查看集合中每个文本的Distance属性,如果某个文本的该属性值为0,则计算出此文本至d的距离.从这K+1个文本中找出距离待分类文本距离最近的新基点dn+1;

6)如果dn+1不等于dn,则令dn为dn+1,并转入步骤5);

7)记录dn+1及距离其最近的K个向量,记为组G1;

8)对于其余的分类c2,c3,…,cM，重复步骤3)～7).对于组G1,G2,…,GM中的文本，按照传统的KNN算法进行分类,以计算出待分类文本d的所属类别Cd.

3 实验结果

一般在信息检索领域,准确率和召回率被认为是一对相互制约的指标,考虑到准确率和召回率并不具有相互独立性且一般呈互逆相关关系,所以更多时候将这两个指标综合考虑.一个融合了准确率和召回率的指标是F值,它是准确率和召回率的调和平均值[5].在文中的分类评价标准中,也采用这3个指标来衡量.

文中实验所采用的操作系统是Windows XP.CPU是Pentium(R) Dual-Core T440 @2.2 GHz.内存大小为2 GB.实验采用的开发工具是Microsoft Visual Studio 2008.开发语言是C++.实验中用到的其他开发工具包括中科院计算技术研究所的中文分词系统ICTCLAS以及开源库Boost C++.

文本实验所采用的语料库主要来自于搜狗语料库,其下载地址为http://www.sogou.com/labs/dl/t.html.在实验过程中将文本分为历史、教育、文化、军事、社会法律、娱乐和IT 7类,采用了语料库中的350篇文本作为训练集(每个类别采用了50篇文本).剩下的文本作为测试集.

在实验中分别采用传统的KNN算法和改进型的KNN算法对数据源做了以下对比实验.首先针对不同K值,对分类效果做了对比,其实验目的是为了找出最优的参数K值,实验结果如表2;其次,取K值为9,对传统的KNN算法以及文本提出的改进的KNN算法做了对比实验,实验结果如表3;最后,在K的不同取值,对两种算法在时间消耗做了对比实验,实验结果如表4.

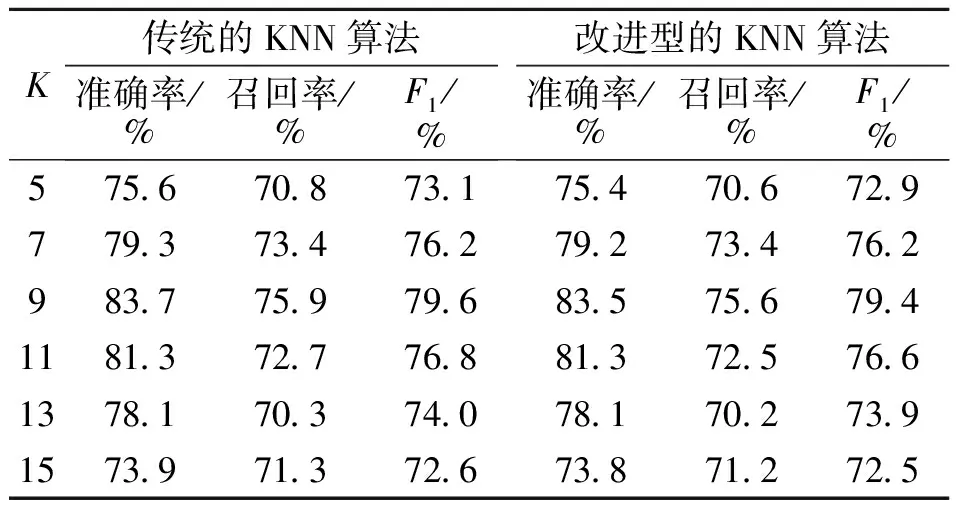
表2 不同K值的分类效果对比Table 2 Contrast results of different K value

通过该组对比实验可以看出,不同K值对于分类的各项性能的影响明显不同.表2中,当K值为9时,无论是在准确率还是召回率上,两种算法的实验性能都可以到达一个顶点.这里值得注意的一点是,同样是针对中文文本及网页分类,不同的研究者在不同的数据源上实验得出的最优K值均有差异[6-7].体现出了KNN算法很难给出一个通用的最优K值,需要根据实验不断地调整.这在一定程度上限制了KNN算法的应用.

表3 传统KNN算法和改进型KNN算法的性能比较Table 3 Performance comparison of traditional KNN algorithm and improved KNN algorithm

通过该组对比实验可以发现,在分类F1值性能上,文中提出的改进型KNN算法要比传统的KNN算法略差,这主要是因为文中提出的算法,在查找距测试向量最近的K个向量时,可能会有遗漏某些向量.但是可以看出两种算法在此性能上的差别很小,这是因为在分类策略上,两者完全一致.在实际应用中,精度性能上的细微差别可以忽略.

表4 传统KNN算法和改进型KNN算法的时间消耗比较Table 4 Time consuming comparison of traditional KNN algorithm and improved KNN algorithm

通过该组对比试验,可以发现,在K的各种取值下,文中所提出的改进型KNN算法在时间开销上都具有明显的优势.这也说明了该算法是行之有效的，可以较好地解决传统KNN算法在计算时,时间消耗大的问题.当然,取得这一优点的代价是改进型的KNN算法需要在训练阶段消耗时间,这一时间消耗是明显要高于传统KNN算法的.

4 结论

文中提出的改进型的KNN算法在计算复杂度上由于改进了对近邻点的搜索策略,能明显地优于传统的KNN算法，具有一定的理论意义和实际应用价值.同时在对于初始点的选取上是选取了各个类别的中心,相比于传统的KNN算法,更适合采用并行计算结构.这也是下一步需要考虑的研究工作.

[1] 苏金树,张博锋,徐昕.基于机器学习的文本分类技术研究进展[J].软件学报,2006,17(9):1848-1859.

Su Jinshu,Zhang Bofeng,Xu Xin.Advances in machine learning based text categorization[J].JournalofSoftware,2006,17(9):1848-1859.(in Chinese)

[2] Cover T M, Hart P E. Nearest neighbor pattern classification[J].IEEETransactionsonInformationTheory,1967, 13(1): 21-27.

[3] 张野,杨建林.基于KNN和SVM的中文文本自动分类研究[J].情报科学,2011,29(9):1313-1317.

Zhang Ye,Yang Jianlin.Research on automatic classification for Chinese text based on KNN and SVM[J].InformationScience, 2011,29(9):1313-1317.(in Chinese)

[4] 王爱平,徐晓燕,国玮玮,等.基于改进KNN算法的中文文本分类方法[J].微型机与应用,2011,30(18):8-10.

Wang Aiping, Xu Xiaoyan, Guo Weiwei,et al.Text categorization method based on improved KNN algorithm[J].Microcomputer&ItsApplications,2011,30(18):8-10. (in Chinese)

[5] Manning C D. 信息检索导论[M]. 王斌，译.北京:人民邮电出版社,2010:187-188.

[6] 刘应东,牛惠民.基于k-最近邻图的小样本KNN分类算法[J].计算机工程.2011,37(9):199-200.

Liu Yingdong,Niu Huimin.KNN classification algorithm based on k-nearest neighbor graph for small sample[J].ComputerEngineering,2011,37(9):199-200. (in Chinese)

[7] 鲁婷,王浩,姚宏亮.一种基于中心文档的KNN中文文本分类算法[J].计算机工程与应用.2011,47(2):127-130.

Lu Ting,Wang Hao,Yao Hongliang.K-nearest neighbor Chinese text categorization algorithm based on center documents[J].ComputerEngineeringandApplication,2011,47(2):127-130. (in Chinese)